Robust Service Time Measurement Using Comparison Sequential Test ()
1. Introduction
The theme of the paper was dictated by experimental design problems attendant on the assessment of the effect of innovations in the parameters of the service process run by information technology systems (IT)―for example, the one client service time (OCST).
The need for simultaneous comparison testing in such a case arises from the rapidly changing conditions of the server activity [1] , so that a reference is necessary to assess the effectiveness of an innovation, or (for example) that of training a new server group at a call centre [2] . For this purpose a comparison test is available [3] in which two systems are involved, one of which is tested as innovative in some respect, and the other used as the reference. The underlying assumption is that the TBE in both items is exponentially distributed. On practice this assumption looks overly constraining.
The OCST can have a variety of distributions. For example, Brown et al. [4] assign to it a lognormal one with a CV (the ratio of the standard deviation and expectation) exceeding 1. The throughput capacity of the service process is frequently increased by recourse to a group of servers carrying out identical functions. This service process we shall present as a stream of events, which terminates in the completion of service to a client [1] . The unified stream of such events will have a distribution close to the exponential by Palm-Khinchine theorem [5] - [8] . If the test is run during the period of heaviest traffic of the workday, when clients have to wait in a queue and the servers are fully engaged, the above service process depends only on the OCST and the group size, so that the assessment problem is reduced to comparison of the mean TBE’s (MTBE) of two such processes.
In [3] , it was shown that the above comparison test was reduced to the binomial sequential probability ratio test (SPRT), first described by Wald [9] . Its advantage is that it needs a substantially smaller average sample number (ASN) for a decision to be taken [10] . The idea of the sequential test is that after each step one of three decisions is made: accept null hypothesis and finish test, or reject null hypothesis and finish test, or proceed with the test for further refinement.
The natural question was how the characteristics of the test will change on deviation from the TBE of the exponential distributions for the processes under comparison.
Analogous problems arise in other fields, for example, in testing for reliability [3] [11] , where the TBE is often other than exponential [12] , with high uncertainty as for the actual distribution.
The planning aspects of the comparison SPRT (CSPRT) for a pair of streams with exponential TBE’s have been addressed rather in full [13] - [18] , but a still open topic of particular interest is the influence of deviations from exponentiality on the test characteristics. This influence determines the robustness of the test, which is critical in the practical application of the latter.
The earliest approach to the SPRT’s robustness is due to Wald [9] , who formulated a requirement for the test whereby the I- and II-kind error probabilities (α, β) should not exceed prescribed limits instead of being specifically set. Usually, the term robustness is associated with small deviations of α and β from the nominal, under small departures from the model assumptions [19] - [22] . The checked characteristics sometimes include also the ASN (Quang [23] ). In practical terms, however, of greater interest is the following presentation of the problem, which is close to Wald’s approach: are the test characteristics (say α, β and ASN) not worse (or only insignificantly worse), than the nominal within the practically relevant range of departures from model assumptions (such as exponentiality of the TBE).
Harter and Moore [24] ran a computer experiment with a view to verifying that the parameter of the exponential distribution (MTBE) is not less than the prescribed value, and noted the criticality of robustness in the practical application of the test. In their paper, the above authors concluded that for the TBE’s distributions satisfying Weibull’s law (considered instead of exponentially) α, and β decrease with an increase of the shape parameter SWeib, with SWeib > 1, and become less than the nominal values, while decreasing significantly with an increase of SWeib. Based on that, the authors concluded that the test is not robust; although cases with SWeib > 1 are common, a decrease in α and β improves the credibility of the findings. Another limitation of this work is that the results relate only to the Weibull distribution, although in practice it is difficult to determine its actual distribution. Thus it is preferable to have a factor not associated with a specific distribution.
The above case was treated theoretically by Montagne and Singpurwalla [25] , with the behaviour of the hazard function (events rate) chosen as a defining characteristic of robustness. In that work the authors caution about the effect of α and β reduction on the interpretation of the tests and its possible effect on practical tests. To establish robustness they use monotonicity of the hazard function. These results are difficult to apply to distributions whose hazard function is not monotonic, such as the lognormal often encountered in practice [4] [12] .
In this work, we investigate the dependence of robustness on the coefficient of variation CV (the ratio of the standard deviation and expectation). This parameterization allows us to describe robustness in terms of one value and not of the whole function (like the hazard function), thus there is no need to require monotonicity of the hazard function.
The results obtained in the above studies are not relevant to CSPRT, as the latter is designed to compare two processes, each of which is characterized by its distribution.
The next step in extending the results for more general case, the so-called life distribution, was carried out by [26] . In that paper the expression for the domain of robustness becomes much less tractable due to generality of the addressed distributions. By contrast, in our paper we are concerned with domains of robustness where error probabilities do not increase significantly, although we allow those values to drop.
More characterizations of double-sided robustness that is robustness that controls both significant reductions and increases of the test’s characteristics (for example α, and β) were done in [27] . There, a sufficient condition for the double-sided robustness is expressed under a mild additional requirement. We are more concerned with one-sided robustness and suggest characterization of the robustness domain in terms of CV.
Robustness of SPRT under small convex perturbation by noise was considered by Kharin and Kishylau [7] . This type of perturbation as a rule leads to distributions outside of the parametrised family of distributions. By contrast, we are interested in robustness under perturbation of parameters of the distribution.
It is advisable to assess the robustness of the discussed CSPRT in comparison with other tests that can be used as an alternative. The problem of comparison testing can be solved with the FSST, whose description goes back to Mace [28] . The FSST continues until a predetermined sample size (number, SN), and then the null hypothesis is verified. The test is uniformly most powerful for a given SN, i.e. in a certain sense it is optimal (Ghosh [29] , Section 1.3). Thus, it is often used for comparative assessment of other tests [30] .
Representative distributions of service time are lognormal [4] [31] , exponential [32] , hyper-exponential (a mixture of exponential distributions) [33] , Erlang’s [34] [35] . TBE distributions for the superposition of events streams from the large number of servers (streams superposition) [1] are exponential or near exponential, even though the service time distribution for each server is not quite similar to the exponential [5] . For a small number of superposed streams, the TBE can be approximated by Weibull and gamma distributions [1] .
Based on the above, we can draw the following conclusions:
・ Robustness is crucial for the practical application of the test.
・ For the suggested CSPRT there are no studies concerned with its robustness.
・ For the test under consideration the usability of CV as a strong factor affecting the robustness needs to be verified. The significant advantage of CV is that it is a simple measure not associated with a specific distribution.
・ The robustness of the CSPRT must be evaluated in comparison with the FSST.
・ Robustness should be assessed for the most typical TBE distributions: Weibull, gamma, lognormal.
Contributions of the paper:
・ We suggest a novel criterion that allows analysing robustness of the test. We show that the main factor influencing these characteristics is CV of the TBEs. Just by using CV of the TBEs we may conclude whether the test is robust or not. Note that CV is easy to evaluate in practice.
・ We also suggest approach of handling the case when test for pair of single TBEs is not robust (case of CV > 1). Transition from a single server to a group of servers and from a single stream to a superposed stream of events improves robustness, since superposition of event streams brings the TBEs’ distribution closer to the exponential.
・ The analytical dependency of the fixed sample size test (FSST) robustness vs. CV permits simple estimation of robustness of the test in question. The advantage of the test vs. the FSST is shown, and illustrated on a real-life case.
2. Description of Comparison Tests and Evaluation Methodology of Their Robustness
2.1. Comparison Sequential Probability Ratio Test (CSPRT)
2.1.1. Description of CSPRT
The purpose of the CSPRT test is to verify the hypothesis Н0 about the MTBE ratio Φ for the new (marked qnew) and the reference (marked qref) items:
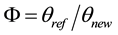 (1)
(1)
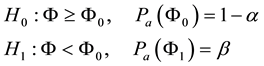 (2)
(2)
where Pa(F)―the acceptance probability of H0 at given F (the operational characteristic―OC of the test), and
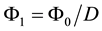 (3)
(3)
where D > 1 is the discrimination ratio of the test; Φ0, D, α, β―are fixed.
The CSPRT procedure including optimal parameters’ choice was suggested in [36] and developed in full details in papers [3] [13] - [15] .
During the CSPRT two compared items are tested simultaneously (Figure 1) [3] . When an event occurs with one of the items, it immediately goes into the initial state. At this point, the decision is made either to stop the test and accept/reject the hypothesis H0, or to continue the test until the next event.
As applied, for example, to the work of an IT service centre, an “item” is the group of servers, an “event”― completion of service to a client, and an “initial state”―beginning of service to the next client. The assumption here is that there is a workload for all servers.
For the test in question with exponential TBE, the estimate of Φ is time-invariant and changes only at the moment of an event with one of the items, [3] . The probability PR(Φ) that the next event will occur with the reference item is calculated as the probability that one random variable is greater than the other, or:
 (4)
(4)
This permits presentation of the tests in binomial form and their reduction to the well-known SPRT [3] [10] . Figure 2 shows the test space in discrete coordinates (n, r) which are the new and reference item number of events respectively. The test begins at point (0,0) and with each event in either item, moves one step to the right (new item) or upward (reference item). In terms of the binomial test that verifies hypotheses (2), events with a new item correspond to a success and events with a reference item―to a failure. The probability of an upward step towards the reject boundary, irrespective of the point’s coordinates, is given by (4).
The test stops when it leaves the continue zone, bounded by parallel oblique boundaries and by truncation lines parallel to the coordinate axes. H0 is accepted when the lower and right-hand boundary is crossed a point denoted ADP―Accept Decision Point and is rejected when the upper and left-hand boundary is crossed at RDP―Reject Decision Point. Originally, the theory of Wald’s SPRT did not include truncation, and as a result there was a possibility that the test would continue much longer than the average duration. Truncation is used to limit the duration and remove this drawback [1] [16] . The boundaries are plotted according to principles outlined in Wald [10] .
2.1.2. Methodology of CSPRT Robustness Estimation
We used the Monte Carlo method to establish robustness of the CSRPT for non-exponential distributions of ТBЕref and TBEnew. We considered a CSPRT with known Accept/Reject lines, hence with known ОС and ASN, for exponential TBEs. We applied the obtained test to the TBEs corresponding to a non-exponential distribution belonging to one of the frequently-used families. Note that in the general case the probabilities PR of a step up depend on both the time elapsed since the last step up and that elapsed since the last step to the right. Hence the test requires that the whole set of TBEs be considered. This was achieved as follows.
Simulation was implemented as shown in Figure 1. The time intervals between the steps for the reference and new items ТBЕref and TBEnew were generated using given distributions. Moving from T = 0 along the T axis,
![]()
Figure 1. Scheme of test course. Note. Upward marks―events of the reference item; downward marks―those of the new item; T―time axis, common to both items; ADP―accept decision point.
![]()
Figure 2. Plan of truncated CSPRT and example of test course. Note. The characteristics of CSPRT for hypothesis (2): a = 0.2, b = 0.1, D = 3, Φ0 = 1. In terms of the binomial test n―success number and r―failure number. TA―truncation apex.
each point representing an event in the reference item (upward marks, Figure 1) matched an upward step in Figure 2, and one representing an event in the new item (downward marks) ? a step to the right, and so on until the Accept or Reject boundary was crossed. At this juncture the test was stopped and the final point recorded. The results from a large number of simulation runs yielded the OC and ASN of the test.
2.2. Comparison Fixed Sample Size Test (FSST)
2.2.1. Description and Calculation Methodology for FSST Parameters
Mace [28] describes a test for checking the hypotheses (2), which continues up to a pre-set SN, namely r and n for the reference and new items respectively, not necessarily equal. When these SN have been reached, a decision is taken on acceptance/rejection of the null hypothesis.
Let us denote by Tnew and Tref the total working times of the respective items, up to stopping of the test. When the TBE distribution is exponential, 2Tref/θref and 2Tnew/θnew have an χ2-distribution with 2r and 2n degrees of freedom respectively, and the [Tref/(2rθref)]/[Tnew/(2nθnew)] ratio obeys an F-distribution with the same degrees of freedom.
The null hypothesis (2) is accepted when (5) is satisfied, and rejected in the opposite case:
F > с (5)
where
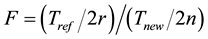 (6)
(6)
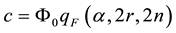 (7)
(7)
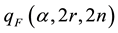 -quantile of F-distribution with 2r, and 2n degrees of freedom at probability α. The necessary n and r are obtainable as per
-quantile of F-distribution with 2r, and 2n degrees of freedom at probability α. The necessary n and r are obtainable as per
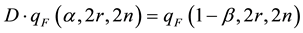 (8)
(8)
This calculation requires that a ratio be set between n and r, e.g. on the basis of the expected rates of events from the compared items [16] . If the rates are close, it is reasonable to set n = r.
2.2.2. Methodology of FSST Robustness Evaluation
For 2r → ∞, the χ2-distribution converges to the normal and respectively the normalization Tref/(rθref) converges to the normal with expectation 1 and standard deviation 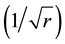
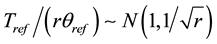 (9)
(9)
The 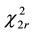 -distributed random value can be presented as the sum of 2r i.i.d. random variables. It is usually accepted that for 2r > 30, the resulting distribution is sufficiently close to the normal.
-distributed random value can be presented as the sum of 2r i.i.d. random variables. It is usually accepted that for 2r > 30, the resulting distribution is sufficiently close to the normal.
For an exponential distribution, CV = 1. For other distributions, CV can differ from 1 and accordingly
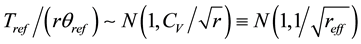
where reff is the effective number of events
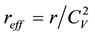 (10)
(10)
All the above hold for Tnew and neff; hence for (r > 15) & (n > 15) the robustness of the FSST can be evaluated through αreal and βreal as follows:
・ Calculating r, n, c by (7)-(8) for specified α, and β.
・ Calculating reff, neff by (9)-(10) for specified CV.
・ Calculating αreal, and βreal by (11) for the reff, neff, c found above.
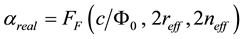 , (11)
, (11)
where![]() ―cumulative function of F distribution with 2reff, and 2neff degrees of freedom.
―cumulative function of F distribution with 2reff, and 2neff degrees of freedom.
When CV < 1 for both input event streams, the degrees of freedom in (11) increase in accordance with (10); hence αreal, and βreal are less than their nominal counterparts. In other words, the FSST is robust at CV ≤ 1 for both streams.
Subsection 3.3 presents a calculation example illustrating this conclusion.
3. Robustness of the CSPRT for Various Distributions of TBEs. Comparison with FSST
We illustrate the study on the test example with the following nominal characteristics (i.e. those for exponential TBEs):
Φ0 = 1, D = 1.5, αreal = 0.10, βreal = 0.10 (12)
The parameters of the boundary for the test (after the example in Figure 2) are:
Accept line: min[n = (r+12.66)/1.224; n = 117],
Reject line: min[r = 1.224 × n + 12.39; r = 95];
here n = 117 and r = 95 are the TA’s coordinates (Figure 2).
Since the results for αreal and βreal are similar, the figures show only those for αreal. Due to the similarity of the results for the Weibull, gamma and lognormal distributions, we provide figures only for the Weibull.
Note that for the Weibull and gamma distributions, the hazard function is monotonic. In this case our results are similar to those [25] concerning the robustness of non-comparison tests. For the lognormal distribution, the hazard function is not monotonic, and the methods of [25] are not applicable even in the case of non-comparison tests.
3.1. Robustness of the CSPRT for Weibull-Distributed TBEs
Figure 3, Figure 4 present a calculation example of the test characteristics (αreal, ASN(Φ0)) for Weibull-distri- buted TBEs and different shape factors. The nominal characteristics of the test were as in (12). In the above figures these values (12) are reached at WeibShapenew = WeibShaperef = 1. The behaviour of βreal is analogous to that of αreal in Figure 3.
Figure 3 indicates that deviations of the TBE distributions from the exponential have a strong effect on the
![]()
Figure 3. αreal of CSPRT vs. shape factors of Weibull-distributed TBEs of new and reference items for the test with nominal characteristics (12).
![]()
Figure 4. Contour plot for ASN(Φ0) Note. Under the same conditions as Figure 3.
test characteristics. At the same time, increase of the shape factor above 1 results in a substantially improved OC (smaller αreal, and βreal). A slight reduction below 1 in one of the shape factors, combined with an increase in the other above 1, does not cause deterioration of the OC versus the nominal. The test’s ASN (Figure 4) decreases when both factors decrease below 1, and slightly increases when the factors increase above 1. Note that the maximal test duration remains the same.
3.2. Coefficient of Variation Influence
The analysis of dependences of αreal, and βreal on form parameters of non-exponential distributions of TBE, following the steps outlined in Subsections 3.1 showed that the CV is the most significant factor affecting variation of αreal, and βreal.
In Figure 5 the contour plots are shown for dependences of αreal on CV of TBEs compared flows for the three distributions: Weibull, gamma, and lognormal. These graphs are almost identical, especially the Weibull and gamma. The dependences for βreal are similar. In summary, we conclude that αreal, and βreal are almost independent of the type of TBE distribution, and completely determined by their CV.
The line αreal = 0.1 in Figure 5 is an example of the robustness onset border for the CSPRT. The graphs show that decrease of CV below 1 dramatically reduces the probability of the wrong decision. Some increase in CV over 1 for one of the compared TBE stream distributions, while reducing CV for another stream, does not degrade the characteristics of the CSPRT. Emergence outside the curve αreal = 0.1 results in their significant deterioration.
3.3. Robustness of FSST and Comparison with CSPRT
In this subsection, we evaluate the robustness of FSST. Note that for this test we are able to provide a good approximation and a closed-form solution without use of simulation (see Subsection 2.2).
The methodology presented in Subsection 2.2.2 yielded the parameters for an FSST with characteristics (12).
As per (7)-(8), the following was obtained:
r = n = 81, с = 0.816 (13)
Figure 6 presents the results for the relevant αreal, βreal vs CV, which is the same for both TBEref and TBEnew. Accordingly, it was found that αreal = βreal (FSST curve). It is seen that αreal, and βreal are less than (i.e. superior to) their nominal counterparts at CV < 1; in other words, under these conditions the FSST is robust.
Figure 6 contains also the data for the CSPRT with characteristics (12) and with Weibull-distributed TBEs. This test is described in detail in Subsections 2.1 and 3.1. It is seen that the tests are practically equivalent in terms of robustness, but the ASN of the CSPRT (see Figure 4) is substantially less than the SN of the FSST (SN = r + n = 162). The proximity of the dependences of αreal, βreal vs CV for the CSPRT and FSST makes possible an
![]()
Figure 5. CSPRT. Contour plot of αreal vs CV of TBEs for various distributions of TBFs. Notes. The test with nominal characteristics (12). Weibull―continuous lines, gamma―the dottedlines, lognormal―dashed-dottedlines.
![]()
Figure 6. αreal, βreal vs. CV of TBEs of both compared streams. Note. The tests with nominal characteristics (12).
analytical estimate of CSPRT robustness based on CV of the TBE distributions.
4. Stream Superposition for CSPRT Application for CV > 1
As follows from the preceding Section, direct application of CSPRT to the assessment of OCST is inefficient, since the OCST is usually characterized by a lognormal TBE distribution with CV significantly exceeding 1. In other words, αreal and βreal of CSPRT are significantly greater than nominal, hence the test is not robust.
However, it is possible to use CSPRT to compare the mean OCST of two groups of servers. In this case, the superposition of streams from one server group (Figure 7) forms a stream with TBE distribution close to exponential. In [1] it was shown that the stream distribution of TBEs obtained upon superposition of 15 or more server streams does not essentially differ from the exponential, even when the OCST distribution is far from exponential. In other words, the test with superposed input streams becomes more robust. The larger the number of the superposed streams, the closer to the original is the test’s characteristics. We submitted a patent application for this testing method.
5. Application to a Real Life Example
5.1. Design of the Test
Our results, described earlier in the paper, were applied to the design of the experiment for the performance evaluation in the call centre of a large IT corporation.
The purpose of the experiment is to establish if innovation consisting in automation of some probes and scripts that are usually run by a service associate (server) may improve the overall average tickets processing time.
As the medium of service requests is fast changing, it is natural to assign the processing to two groups working in parallel, one for testing the new technology and the other as a reference.
The experiment for hypothesis (2) was set for the following:
Φ0 = 1.10, Φ1 = 1.01, α = 0.1, β = 0.1 (14)
In other words, if the suggested innovation reduces the overall average tickets’ processing time by 10% (or Φ0 = 1.10, see (1)), then the probability of rejecting H0 erroneously should be α = 0.1. Moreover, if the reduction is only by 1% (i.e. Φ1 = 1.01), then the probability of accepting H0 erroneously should be β = 0.1.
Applying the methodology described in [37] and under an exponential distribution of the OCST, the binomial SPRT with OC and ASN as per Figure 8 was designed. Figure 8 also shows a SN of the FSST, evaluated by the results of Subsection 2.2.1. The parameters of the boundary for the test (after the example in Figure 2) are:
![]() (15)
(15)
![]()
Figure 7. Streams superposition: (a), (b)―streams from single servers, (c)―resulting superimposed stream.
![]()
Figure 8. OC and ASN of the test with boundaries as in (15) under assumption of the exponentially distributed TBE. Note. Pa is the OC of the test; CSPRT truncation―by TA (see Figure 2).
here n = 2309 and r = 2191 are the TA’s coordinates (Figure 2).
5.2. A Priori Information about Streams under Comparison
Before running the experiment we collected information about the distribution of the OCST of the reference technology. The mean value of the OCST is μOCST = 23 min and the coefficient of variation CV_OCST = 1.19. Figure 9 shows the cumulative distribution of the OCST and its lognormal fitting.
Comparing this data with Figure 5, it is clear that for such event streams the binomial SPRT is inefficient, since αreal and βreal will be significantly above their targets. This is why we apply this test to the merged streams as indicated below.
5.3. Test Setup
Based on the actual capabilities of the call centre, each of the groups under comparison consisted of 8 servers. When necessary these servers were replaced with others working under the same technology. This enabled the groups of servers to work continuously until the test was completed. The excess of the tickets were redirected to other groups that we do not consider here.
Since processing time exceeds 85 min on very rare occasions (Figure 9), such a ticket is transferred to the server of the highest level (and hence more competent).
After a ticket was processed, the end times of processing were merged into one stream of events. For all 8 servers, the MTBE in the resulting stream was approximately 23/8 = 2.9 min. The TBE of the stream was close to exponential as predicted by the Palm-Khinchine theorem; hence we can apply the binomial SPRT.
5.4. Simulation-Based Estimate of the Test Characteristics
This estimate was obtained under the above-mentioned assumption of the non-exponential OCST (Figure 9). Both α and β were increased to 0.11 compared with the target (14). These increases are satisfactory from a prac-
![]()
Figure 9. Cumulative distribution function of the OCST (one client service time) and its lognormal fitting.
![]()
Figure 10. Simulation results for Expected Duration (ED) of CSPRT and Duration (D) of FSST.
tical point of view. The ASN showed a reduction by approximately 5%. Note that the increased number of servers improves the properties of the test. Figure 10 shows the expected duration of the test for MTBEref = 2.9 min. It also shows an estimate of the FSST duration with α = β = 0.11 and illustrates a significant advantage of the suggested CSPRT over the FSST. We run extended simulation with 10’s of thousands tests simulations; the number of tests simulations was determined by relative error in α and β do not exceed 1% to get understanding of the system behaviour.
Note that the results of the case study confirm the conclusion of the paper.
6. Conclusions
1) Innovation in service delivery processes, in terms of reduced mean service time, can be assessed through the Comparison SPRT (CSPRT), which, on the average, is faster than the alternative FSST.
2) As the CSPRT is designed on the assumption of an exponential distribution of the TBE, we study its robustness and that of its alternative FSST under various distributions of the compared TBEs.
3) It is shown that the main influencing factor for the test characteristics is the coefficients of variation (CV) of the TBEs. This effect is weakly connected to other parameters of the TBE distributions.
4) For the proposed CSPRT, reduction of the TBEs’ CV to less than 1 makes for drastic improvement in its OC (reduced αreal, βreal). In other words, in these cases the CSPRT can be rated as robust. It is not robust when CV are significantly greater than 1 for both streams under comparison. The CSPRT may be applied for comparison of the mean service time for two groups, since superposition of event streams for each group has a distribution close to the exponential; in other words, the CSPRT is robust under these conditions. We submit a patent application for that method of testing.
5) The comparison FSST manifests robustness like the CSPRT, but its sample number is substantially larger than the ASN of the CSPRT.
6) The analytical dependency of the FSST’s robustness on CV permits simple estimation of that of the CSPRT.
Acknowledgements
The research project was supported by the Israel Ministry of Absorption and the Planning and Budgeting Committee of the Israel Council for Higher Education.
NOTES
*Corresponding author.