New Electronically-Controllable Lossless Synthetic Floating Inductance Circuit Using Single VDCC ()
1. Introduction
Although many circuits for the simulation of grounded and floating inductance using different active building blocks such as operational amplifiers [1-5], current conveyors [6-13], current feedback amplifiers [14,15], current differencing buffered amplifiers [16,17], current differencing transconductance amplifiers [18,19], operational transconductance amplifiers [20,21], operational mirrored amplifiers [22], voltage differencing differential input buffered amplifiers [23,24], and voltage differencing transconductance amplifier [25] have been reported in the literature. In [26], many active building blocks have been presented, and VDCC is one of them. The usefulness of recently introduced active building block “VDCC” is well-defined in [27]. In [27], the authors proposed grounded inductance simulator circuits using single VDCC and two passive components. To the best knowledge of the author, no floating inductance simulator circuit using single VDCC and two passive components has been reported in the open literature so far.
Therefore, the main objective of this paper is to propose a new circuit which employs one VDCC, one grounded capacitor and one grounded resistor to realize electronically-controllable lossless matchless FI circuit. The presented circuit has also the features like only two passive components (i.e. one grounded capacitor (as desired for IC implementation) and one grounded resistor) and low active and passive sensitivities. The validity of the presented new circuit has been verified using SPICE simulation with TSMC CMOS 0.18 μm process parameters.
2. The Proposed New Configuration
The symbolic notation of recently proposed active building block, VDCC is shown in Figure 1, where P and N are input terminals and Z, X, WP and WN are output terminals. All of the terminals exhibit high impedance, except the X terminals [27]. The VDCC is characterized by the Equation (1).
Figure 1. The symbolic notation of VDCC.
(1)
The proposed FI circuit is shown in Figure 2.
A routine circuit analysis of the new FI circuit shown in Figure 2 yields
(2)
which shows that the circuit simulates a floating lossless electronically-controllable inductance with the inducbtance value given by
(3)
3. Non-Ideal Analysis and Sensitivity Performance
The proposed FI circuit consisting various non-ideal parasitics is shown in Figure 3. The X-terminal parasitic impedance consisting of a resistance 
in series with inductance
, the parasitic impedance at the WP-terminal consisting of a resistance 
in parallel with capacitance
, the parasitic impedance at the WN- terminal consisting of a resistance 
in parallel with capacitance 
and the parasitic impedance at the Zterminal consisting of a resistance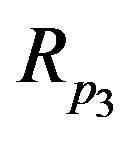
.
For the circuit shown in Figure 3, the input-output currents and voltages relationship is given by
(4)
where
Figure 2. Proposed FI circuit.
Figure 3. Proposed FI circuit including parasitic.
The non-ideal equivalent circuit of FI of Figure 3 is derivable from Equation (4) and is shown in Figure 4.
Where 
and
, 
, 
The various sensitivities of LFI with respect to active and passive elements are:
(5)
Thus, all the passive and active sensitivities of FI circuit are low.
Figure 4. Non-ideal equivalent circuit of Figure 3.
4. Application Examples of New FI Circuit
The workability of the proposed FI circuits are demonstrated by realizing (i) a band pass filter (BPF) (Figure 5) and (ii) a fourth order Butterworth low pass filter with a cutoff frequency 500 kHz was designed using the normalised proto-type shown in Figure 6 [15].
The transfer function realized by the configuration shown in Figure 5 is given by
(6)
From Equation (6), it is clear that centre frequency is tunable by R2.
The performance of the proposed FI circuit was verified by SPICE simulations. The frequency response of the FI circuit was obtained by using CMOS-based VDCC [27]. The following values were used for FI circuit: C = 0.01 nF, gm = 277.833 μA/V, R = 10 kΩ. From the frequency response of the simulated FI circuit (Figure 7) it has been observed that the inductance value remains constant upto 10 MHz.
The application circuits shown in Figures 5 and 6 were also been simulated using CMOS VDCCs. The component values used were for Figures 5: C1 = 0.01 nF, C2 = 0.02 nF, R1 = 10 kΩ, R2 = 3.6 kΩ, gm = 277.833 μA/V and for Figure 6: RS = RL = 1 KΩ, L1d = 0.2437 mH (gm = 277.833 μA/V, C1 = 0.01 nF, R1 = 6.77 kΩ), L2d = 0.5884 mH (gm = 277.833 μA/V, C2 = 0.01 nF, R1 = 16.225 kΩ), C1d = 0.5884 nF, C2d = 0.2437 nF (after appropriate frequency and impedance scaling). The VDCC were biased with ±0.9 volts D.C. power supplies with IB1 = 50 μA (for gm = 277.833 μA/V). Figures 8 and 9 show the simulated band pass filter and 4th-order Butterworth filter responses respectively. A comparison of proposed FI with other published floating inductor is shown in Table 1.
Thus, the above simulation results confirm the validity of the applications of the proposed FI circuit.
Figure 5. Band pass filter realized by the new FI circuit of Figure 2.
Figure 6. Normalised 4th-order Butterworth Low Pass Filter.
Figure 7. Frequency response of the simulated floating inductor.
Figure 8. Frequency response of BPF using the proposed simulated FI.
Table 1. Comparison of proposed FI circuit with other previously published floating inductors.
Figure 9. Frequency response of 4th-order Butterworth LPF.
5. Conclusions
A new electronically-controllable loss-less FI circuit without any matching condition has been proposed which employs one VDCC, one grounded capacitor and one grounded resistor. The proposed circuit offers the following advantageous features: 1) only two passive components i.e. one grounded capacitor (as desired for IC implementation) and one grounded resistor; 2) no matching condition; 3) fully electronically controllable (by changing bias currents); and 4) low active and passive sensitivities. The SPICE simulation results have confirmed the workability of the new proposed floating inductance circuit.
NOTES