Effect of Sinusoidal Heating on Natural Convection Coupled to Thermal Radiation in a Square Cavity Subjected to Cross Temperature Gradients ()
1. Introduction
Natural convection coupled with surface radiation in closed cavities has been extensively studied using numerical simulations and experiments, owing to the practical importance of such configurations in many engineering applications (convective heat losses from solar collectors, thermal design of buildings, air conditioning and, recently, electronic cooling). The majority of the existing studies, which are of numerical nature, concerned with rectangular cavities where the temperature gradient is either horizontal or vertical, including different kinds of boundary conditions [1-6]. Results of these studies show that radiation affects the dynamical and thermal structures of the fluid, reduces natural convection heat transfer component, and contributes to increase the total amount of heat exchanged in the configurations considered. Most of the works conducted in the past on natural convection coupled with radiation inside rectangular enclosures have been substantially oriented to study unidirectional heat transfers resulting from imposed temperature gradients (due to heat fluxes or temperature differences) either parallel or normal to gravity. In some practical situations, much more complex boundary conditions may be encountered where horizontal and vertical temperature gradients could be simultaneously imposed across the cavity. This justifies the presence of published works where the rectangular cavities are heated from below and cooled from above and simultaneously submitted to various specified thermal boundary conditions at the sidewalls. In the absence of radiation effect, Corcione [7] investigated steady natural convection of airfilled rectangular enclosures heated from below, cooled from above and submitted to various thermal boundary conditions at the sidewalls. With respect to the basic thermal configuration wherein the sidewalls are insulated, the heat transfer rate resulting from the hot bottom wall increases when each adiabatic sidewall is replaced with a cooled one, while showing only slight decreases as such replacement is carried out through a heated sidewall. Cianfrini et al. [8] studied natural convection heat and momentum transfer in air-filled tilted square enclosures with differentially heated opposite walls. The results obtained for the average Nusselt number of the whole cavity were expressed through a semi-empirical dimensionless correlation. More recently, Deng [9] studied laminar natural convection in a two-dimensional square enclosure having two and three discrete heat source—sink pairs on the vertical sidewalls. The effects of the size and the arrangement of the sources and sinks on the fluid flow and heat transfer characteristics were investigated. El Ayachi et al. [10] analyzed the interaction of radiation and natural convection in a square cavity filled with air and discretely heated and cooled from the four walls. In this study, the bottom active wall is at higher temperature than that of the top active wall. As results of their study, compared to pure natural convection, heat transfer across the cavity was found to be enhanced notably with the increase of the active wall emissivity, while the effect of the insulated wall emissivity was insignificant.
In the above-mentioned studies, thermal boundary conditions were assumed to be either steady isothermal or constant heat flux wall conditions. However, in many engineering applications, the energy provided to the system is variable in time and gives rise to unsteady natural-convection flow. Solar collectors and printed circuit boards are examples of such systems submitted to variable thermal boundary conditions. In addition, thermal and dynamical behaviors of a fluid subjected to time-dependent thermal conditions are impossible to predict on the basis of the results obtained with constant temperature or heat flux conditions. This justifies the presence of some works in the literature in which the variable aspect of the thermal boundary conditions was considered. In an earlier study, Lage and Bejan [11] studied theoretically the problem of natural convection in enclosures with one side heated with a pulsating heat flux. They showed that the buoyancy-induced flow resonates to a certain frequency of the pulsating heat input and the resonance phenomenon is characterized by maximum fluctuations observed in the heat transfer evolution with the period of the time-dependent temperature. The numerical results obtained by Lakhal et al. in the case of a square cavity totally [12] or partially [13] heated from below with periodic variable temperatures showed that the resulting flow structure and heat transfer were strongly dependent on the amplitude and the period of the variable temperature. Later, Lakhal et al. [14] studied transient natural convection in a square cavity isothermally cooled from above and partially heated from the side. The heating temperature was varied sinusoidally in time and in a pulsating manner. The pulsating temperature leads to better enhancement of the heat transfer in comparison with that engendered by the sinusoidal varying temperature. Antohe and Lage [15] investigated theoretically and numerically the transport of momentum and heat while considering clear fluid and fully saturated porous medium differentially heated enclosures with a time-periodic pulsating heat flux. The numerical simulations indicated that the natural-convection activity within the enclosure reaches several local maxima for certain values of the heating frequency, referred to as resonance frequency. Kwak and Hyun [16] and Kwak et al. [17] also studied such a resonant phenomenon of natural convection. It was clearly noted from their studies that the resonant frequency might be well predicted by the Brunt-Väisälä frequency, which is characterized by the thermal stratification of a system. The case of convection heat transfer was considered by Abourida et al. for a square cavity filled with air and submitted to variable thermal boundary conditions on its horizontal [18] and vertical [19] walls. Different modes of heating were considered. At high Rayleigh numbers, results reported in [18] showed that the periodic heating can be used to enhance slightly or to reduce notably the heat losses in comparison with the case of constant temperatures. For a cavity with vertical active walls [19], it was reported that the buoyancy-driven flow presents a tendency to enter in resonance with the periodic heating only when the cold temperature is maintained constant. The resonance phenomenon was not encountered when both hot and cold temperatures were varied simultaneously. Douamna et al. [20] considered two-dimensional transient natural convection in a horizontal channel periodically heated from below with a temperature varying sinusoidally with time. Results of the study showed that the three different routes leading to chaos are identified by progressively varying the amplitude and the period of the variable heating temperature. In a recent work, Zhao et al. [21] analyzed transient laminar natural convection induced by two discrete heating elements flush-mounted on one vertical wall of a square enclosure. The resonance frequencies were obtained numerically and predicted by theoretical analysis. More recently, El Ayachi et al. [22] investigated natural convection coupled with thermal radiation in a square cavity, differentially heated with a temperature varying periodically in time. The existence of the resonance phenolmenon was observed in this study and found to be more intensified by increasing the emissivity and the amplitude of the exciting temperature. The critical period of the exciting temperature leading to the resonance phenomenon was found to be independent on the amplitude the excitation and the emissivity of the walls.
The importance of natural convection coupled with thermal radiation in a cavity subjected to periodic boundary conditions in time, is justified by the relevance of such a transitional process to many technological applications. The power supply of electronic circuits by an alternating current, the collectors of solar energy, rooms housing and building hollow blocks, in which recirculation is periodically driven by daily solar heating, are concrete examples.
In our knowledge, works dealing with time periodic combined natural convection-radiation in rectangular cavities subjected to crossed thermal gradients are nonexistent. This work is, therefore, a numerical contribution to the study of natural convection and surface radiation within a square cavity filled with air and discretely heated and cooled, in a periodic manner, from the four walls. The main parameters governing the problem are the emis-sivity of the walls and the characteristics of the exciting temperature (amplitude and period). The effect of these parameters on heat transfer and fluid flow within the cavity is examined.
2. Problem Formulation
The schematic view of the geometry considered in the present study is given in Figure 1. It consists of a square cavity  discretely heated and cooled from the four walls. Two heating modes are considered. In the first one, named SB heating mode, the bottom active element is heated with a temperature varying sinusoidally in time, while the vertical left active element is maintained hot at a constant temperature. In the second mode, called SV heating mode, the vertical hot element temperature varies sinusoidally in time while that of the bottom active wall is considered constant. The inner surfaces, in contact with the fluid, are assumed to be gray, diffuse emitters and reflectors of radiation. The flow is conceived to be laminar, two-dimensional and incompressible with negligible viscous dissipation. All the thermophysical properties of the fluid are assumed constant except the density in the buoyancy term which is assumed to vary linearly with temperature (Boussinesq approximation); such a variation gives rise to the buoyancy forces.
discretely heated and cooled from the four walls. Two heating modes are considered. In the first one, named SB heating mode, the bottom active element is heated with a temperature varying sinusoidally in time, while the vertical left active element is maintained hot at a constant temperature. In the second mode, called SV heating mode, the vertical hot element temperature varies sinusoidally in time while that of the bottom active wall is considered constant. The inner surfaces, in contact with the fluid, are assumed to be gray, diffuse emitters and reflectors of radiation. The flow is conceived to be laminar, two-dimensional and incompressible with negligible viscous dissipation. All the thermophysical properties of the fluid are assumed constant except the density in the buoyancy term which is assumed to vary linearly with temperature (Boussinesq approximation); such a variation gives rise to the buoyancy forces.
Taking into account the above-mentioned assumptions, the non-dimensional governing equations, written in vorticity-stream function formulation, are as follows:
formulation, are as follows:
 (1)
(1)
 (2)
(2)


Figure 1. Studied configuration and imposed thermal excitations.
 (3)
(3)
The dimensionless stream function and the vorticity are related to the non-dimensional velocity components by the following expressions:
 (4)
(4)
2.1. Boundary Conditions
The dimensionless boundary conditions, associated to the problem are such:
 on the cavity walls (5a)
on the cavity walls (5a)
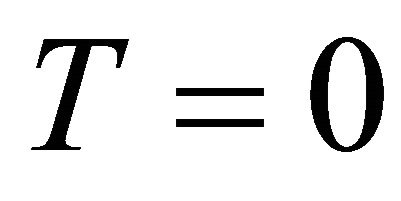 on the cooled elements (5b)
on the cooled elements (5b)
SB Mode
 (5c)
(5c)
SV Mode
 (5d)
(5d)
 (5e)
(5e)
“n” being the normal direction to the considered adiabatic wall.
2.2. Coupling between Radiation and Natural Convection
The working fluid (air) is considered to be perfectly transparent to radiation. Thus air does not participate directly to the radiative heat transfer process (the energy equation remains unchanged) but indirectly via the solid surfaces that are implicated in the radiation exchange. The coupling of the thermal model is performed by computing the radiative exchanges. The calculation of the radiative heat exchange between the internal walls of the cavity is based on the radiosity method. The grid used for convection  is retained in the presence of radiation and consists of 324 isothermal elementary segments. Each segment is sufficiently short to be assumed isothermal. The view factors between the isothermal elementary surfaces were determined by the Hottel’s [23] crossed string method. The summation rules were checked to be sure that the view factors summation equals unity for each surface. The inner surfaces of the enclosure are assumed to be opaque, diffuse and gray. The dimensional radiosity equation for the ith element of the enclosure, in the case of a radiatively non-participating medium is:
is retained in the presence of radiation and consists of 324 isothermal elementary segments. Each segment is sufficiently short to be assumed isothermal. The view factors between the isothermal elementary surfaces were determined by the Hottel’s [23] crossed string method. The summation rules were checked to be sure that the view factors summation equals unity for each surface. The inner surfaces of the enclosure are assumed to be opaque, diffuse and gray. The dimensional radiosity equation for the ith element of the enclosure, in the case of a radiatively non-participating medium is:

 is the outgoing radiation energy flux of the surface Si. It consists of emission, Ei, plus the reflection of incoming energy,
is the outgoing radiation energy flux of the surface Si. It consists of emission, Ei, plus the reflection of incoming energy, .
.
The non-dimensional radiosity equation may be written as:
 (6)
(6)
The non-dimensional net radiative heat flux leaving a surface Si is evaluated by:
2.3. Heat Transfer
 (7)
(7)
At each time step, the mean Nusselt numbers, characterizing the contributions of natural convection and thermal radiation through the heated walls, are evaluated as:
- on the vertical heated wall
 (8)
(8)
 (9)
(9)
- on the horizontal heated wall
 (11)
(11)
 (12)
(12)
The instantaneous convective, radiative and total Nusselt numbers across the whole cavity are defined respectively as:
 (12)
(12)
The mean Nusselt numbers, averaged in time over periods are calculated as:
 (13)
(13)
 (14)
(14)
where tcv and trd are respectively the periods of the temporal variations of convective and radiative Nusselt numbers (they are identical in general).
2.4. Heatlines Formulation
Visualization of the paths followed by the heat flows through the enclosure requires the use of the heatlines concept (lines of constant heat function H). Such lines are defined through the first derivatives of the function H as follows [24]:
 (15)
(15)
The dimensionless heat function equation can be derived easily from Equation (15) as:
 (16)
(16)
Equation (16) is a conduction type problem with a source term becoming zero if the fluid flow subsides (fluid at rest). The solution of Equation (16) yields the values of the heat function in the nodes of the computational domain. The contour plots of the heat function values provide heatline patterns. The H field is defined through its first-order derivatives and only differences of H values are required instead of its intrinsic values. Thus, we have the freedom to state that  (an arbitrary reference value for the heat function H). The boundary conditions for the dimensionless heat function, Equation (16), are obtained by integrating Equation (15) along the considered boundary. The following equations can be used to determine the values of heat function at the walls of the cavity:
(an arbitrary reference value for the heat function H). The boundary conditions for the dimensionless heat function, Equation (16), are obtained by integrating Equation (15) along the considered boundary. The following equations can be used to determine the values of heat function at the walls of the cavity:
 (17)
(17)
3. Method of Solution
The non linear partial differential governing equations, Equations (1)-(3), were discretized using a finite difference technique. First and second spacial derivatives were approximated by means of central differences and the time derivatives by a forward difference. The integration of Equations (1) and (2) was ensured by the Alternating Direction Implicit method (ADI). At each time step, the Poisson equation, Equation (3), was treated by using the Point Successive Over-Relaxation method (PSOR) which with an optimum over-relaxation coefficient equal to 1.92 for the grid adopted in the present study. The set of Equations (6), representing the radiative heat transfer between the different elementary surfaces of the cavity, was solved by using the Gauss-Seidel method. The numerical code was validated against the results of Akiyama and Chong [2] obtained in the case of a square cavity differentially heated. Results of comparisons, made in terms of convective Nusselt numbers, evaluated at the heated wall and presented in Table 1, show a fairly good agreement with relative maximum deviations limited to  for
for  for Ra varying in the range
for Ra varying in the range . Results of a qualitative comparison in terms of isotherms, streamlines and heatlines, against those obtained by Deng [9] are presented in Figure 2 for Ra = 105 and Pr = 0.71 in the case of a square cavity discretely heated and cooled on the four walls without radiation effect; a good qualitative agreement can be seen by comparing these figures. Details relative to the sensitivity of the results vis-à-vis of the grid are given in Table 2. The results presented in this table justify the selected grid of 81 ´ 81 as a reasonable compromise between computational effort and required accuracy. More precisely, the maximum deviations observed in terms of
. Results of a qualitative comparison in terms of isotherms, streamlines and heatlines, against those obtained by Deng [9] are presented in Figure 2 for Ra = 105 and Pr = 0.71 in the case of a square cavity discretely heated and cooled on the four walls without radiation effect; a good qualitative agreement can be seen by comparing these figures. Details relative to the sensitivity of the results vis-à-vis of the grid are given in Table 2. The results presented in this table justify the selected grid of 81 ´ 81 as a reasonable compromise between computational effort and required accuracy. More precisely, the maximum deviations observed in terms of  and
and 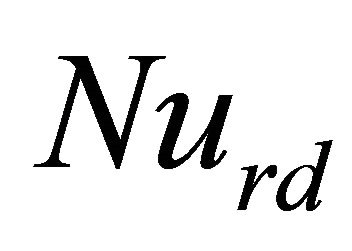 remain within 0.61%, 0.90%, 1.28% and 0.11%, respectively, when the grids of 61 ´ 61 and 101 ´ 101 are considered.
remain within 0.61%, 0.90%, 1.28% and 0.11%, respectively, when the grids of 61 ´ 61 and 101 ´ 101 are considered.
4. Results and Discussion
The main parameters governing the problem are the amplitude of the exciting temperature , it’s period
, it’s period , the emissivity of the walls
, the emissivity of the walls
 , the Prandtl number, Pr, the Rayleigh number, Ra, and the relative length of active elements, B. To highlight the influence of a, t and e, the values of B, Pr and Ra are fixed to 0.5, 0.72 (air) and 106 respectively. In the following, the results obtained are presented in terms of temporal variations of maximum
, the Prandtl number, Pr, the Rayleigh number, Ra, and the relative length of active elements, B. To highlight the influence of a, t and e, the values of B, Pr and Ra are fixed to 0.5, 0.72 (air) and 106 respectively. In the following, the results obtained are presented in terms of temporal variations of maximum  and minimum
and minimum  stream functions and total Nusselt number Nu (Nu being the sum of the convective and radiative Nusselt numbers). The mean values of these quantities, averaged in time over one flow cycle are also discussed to point out the effect of the variable temperature on the coupling between natural convection and surface radiation for both cases of heating considered (SB and SV modes).
stream functions and total Nusselt number Nu (Nu being the sum of the convective and radiative Nusselt numbers). The mean values of these quantities, averaged in time over one flow cycle are also discussed to point out the effect of the variable temperature on the coupling between natural convection and surface radiation for both cases of heating considered (SB and SV modes).

Table 2. Grid sensitivity analysis for Ra = 106 and various values of e.
 (a)
(a) (b)
(b)
Figure 2. Numerical code validation in terms of heatlines in the case of a differentially heated square cavity for Ra = 105 and Pr = 0.7: (a) Deng [9] and (b) Our code.
4.1. Temporal Variation of Ψmin, Ψmax and Nu
For SB and SV heating modes, the evolution with time of Ψmin, Ψmax, and Nu, are presented in Figures 3-5 for  (absence of radiation), various values of a,
(absence of radiation), various values of a, 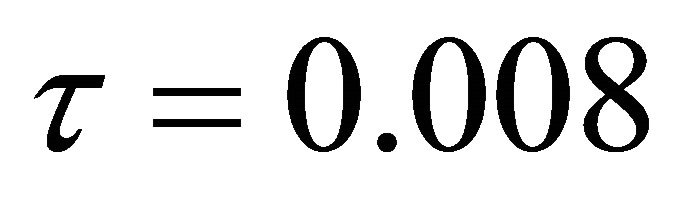 (for SB mode) and
(for SB mode) and  (for SV mode). The choice of these two values of t is guided by a series of tests showing significant effects on fluid flow and heat transfer, which are discussed later. The reference case corresponding to a constant heating temperature (a = 0) is represented in these figures by a continuous horizontal line. Figures 3 and 4 show that, globally the evolution in time of Ψmin and Ψmax is periodic, the amplitudes of the oscillations are visibly enhanced when the amplitude a of the exciting temperature is increased. It can be seen from Figure 3 that, in the case of the SB heating mode, the main flow intensity is higher in comparison to the case of SV heating mode. It can also be noted that the monocellular flow structure, observed for a = 0, disappears in favor of a secondary flow whose size and intensity increase with a (Figure 4). In terms of heat transfer, the increase of the amplitude a is accompanied by a proportional increase in the amplitude of the sinusoidal evolution of Nu (Figure 5).
(for SV mode). The choice of these two values of t is guided by a series of tests showing significant effects on fluid flow and heat transfer, which are discussed later. The reference case corresponding to a constant heating temperature (a = 0) is represented in these figures by a continuous horizontal line. Figures 3 and 4 show that, globally the evolution in time of Ψmin and Ψmax is periodic, the amplitudes of the oscillations are visibly enhanced when the amplitude a of the exciting temperature is increased. It can be seen from Figure 3 that, in the case of the SB heating mode, the main flow intensity is higher in comparison to the case of SV heating mode. It can also be noted that the monocellular flow structure, observed for a = 0, disappears in favor of a secondary flow whose size and intensity increase with a (Figure 4). In terms of heat transfer, the increase of the amplitude a is accompanied by a proportional increase in the amplitude of the sinusoidal evolution of Nu (Figure 5).
The effect of radiation on the temporal variation of Ψmin, Ψmax and Nu is shown in Figures 6-8 in the case of highly emissive walls .
.
The amplitude of Ψmin oscillations is clearly reduced for both heating configuration considered (Figure 6),

Figure 3. Effect of the amplitude a on  for ε = 0.
for ε = 0.
while that of Ψmax is slightly affected, negatively in the case of the SB heating mode and positively in the SV one (Figure 7). It should be noted that for the two heating modes, SB and SV, the clockwise cell, constituting the

Figure 4. Effect of the amplitude a on Ψmin(t) for ε = 0.

Figure 5. Effect of the amplitude a on Nu(t) for ε = 0.
main flow, remains dominant during the evolution of the cycle, while the secondary counterclockwise flow, plays a less important role. For the heat transfer, Figure 8, shows that when radiation of the walls is considered, the amplitude of Nu oscillations, is significantly enhanced; indicating an improvement of the total heat transfer when
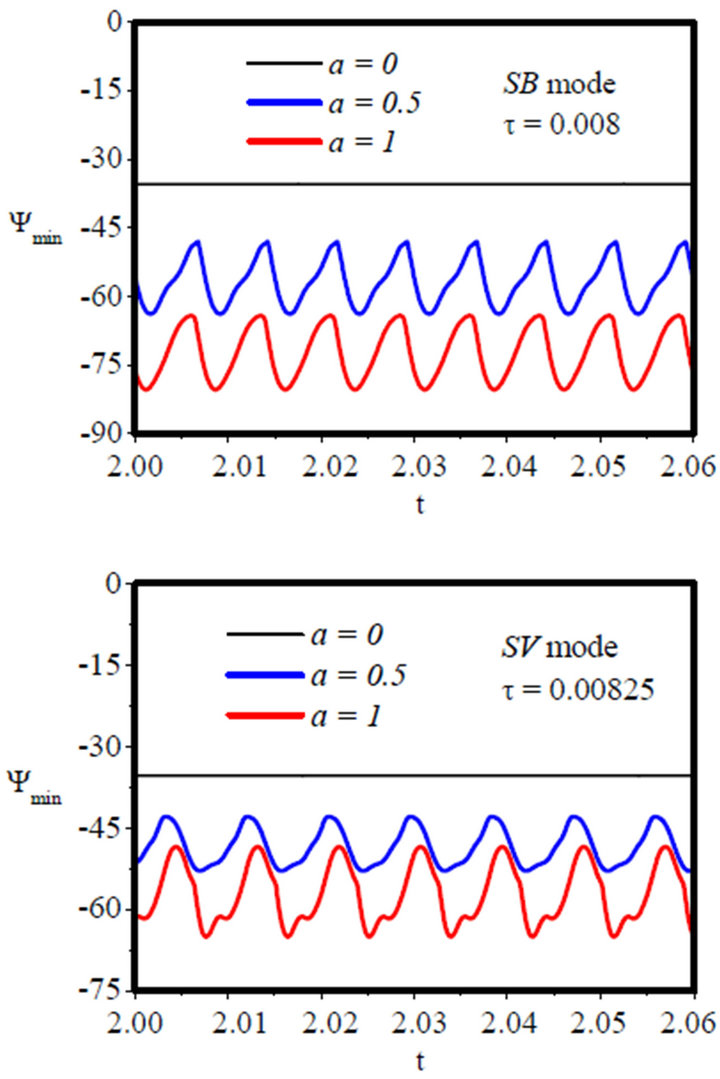
Figure 6. Effect of the amplitude a on Ψmin(t) for ε = 1.

Figure 7. Effect of the amplitude a on Ψmin(t) for ε = 1.
radiation is taken into account.
4.2. Streamlines, Isotherms and Heat-Lines over a Flow Cycle
From the temporal evolution of Ψmax, discussed above, it

Figure 8. Effect of the amplitude a on Nu(t) for ε = 1.
appears that the secondary flow intensity is less important in the case of SV mode than in the SB one. That is why in this subparagraph, the study will be limited to this later configuration. Figures 9 and 10 correspond to the case of constant thermal excitation  and are used as reference, respectively for e = 0 and e = 1.
and are used as reference, respectively for e = 0 and e = 1.
On the other hand, in Figures 11 and 12 are presented the streamlines, isotherms and heatlines, obtained during a flow cycle in the case of sinusoidal exciting temperature , respectively for e = 0 (non-radiative walls) and e = 1 (strongly radiative walls). Also, in Figures 11 and 12, the letters (a), (b), (c), (d) and (e) correspond to the selected times in Figures 4 and 7. As can be seen from Figure 9, the flow is dominated mainly by a large cell zone surrounding three small others located in the central part of the cavity. Once the modulated temperature is applied (a = 1), a fundamental change in the flow structure is observed (Figure 11). Thus, the streamlines show that during the evolution of the cycle, the flow passes through various states characterized by the dominance, at the instant (a), of large clockwise dominant cell and the appearance, at instants (b), (c) and (d), of a secondary counterclockwise cell, small and of
, respectively for e = 0 (non-radiative walls) and e = 1 (strongly radiative walls). Also, in Figures 11 and 12, the letters (a), (b), (c), (d) and (e) correspond to the selected times in Figures 4 and 7. As can be seen from Figure 9, the flow is dominated mainly by a large cell zone surrounding three small others located in the central part of the cavity. Once the modulated temperature is applied (a = 1), a fundamental change in the flow structure is observed (Figure 11). Thus, the streamlines show that during the evolution of the cycle, the flow passes through various states characterized by the dominance, at the instant (a), of large clockwise dominant cell and the appearance, at instants (b), (c) and (d), of a secondary counterclockwise cell, small and of
low intensity in the lower left corner of the cavity. The corresponding isotherms are tightened at the active elements, indicating that the convective heat exchange is good in this region of the cavity. Lines corresponding to heat flux (heatlines) show a similarity with the streamlines and demonstrate the dominance of convective heat transfer (high values of the stream function).
Furthermore, for e = 1 and a = 0, Figure 10 shows a more complex flow structure consisting of a large and intense main cell zone and four small secondary counterclockwise cells taking place in the four corners of the cavity. By introducing a sinusoidal thermal excitation , a specific examination of the streamlines of Figure 12 reveals that the flow structure, during one cycle of evolution, is dominated by a large and intense clockwise cell, surrounded, at the four corners of the cavity, by secondary counterclockwise cells more or less important according to the considered instants. Because of this complexity, the isotherms show a consistent temperature distribution, generally characterized by large thermal gradients in the vicinity of the active elements. Meanwhile, the heatlines show a similar shape to that of the streamlines, reflecting the dominance of convective heat transfer in such a situation.
, a specific examination of the streamlines of Figure 12 reveals that the flow structure, during one cycle of evolution, is dominated by a large and intense clockwise cell, surrounded, at the four corners of the cavity, by secondary counterclockwise cells more or less important according to the considered instants. Because of this complexity, the isotherms show a consistent temperature distribution, generally characterized by large thermal gradients in the vicinity of the active elements. Meanwhile, the heatlines show a similar shape to that of the streamlines, reflecting the dominance of convective heat transfer in such a situation.
4.3. Effect of the Period τ on 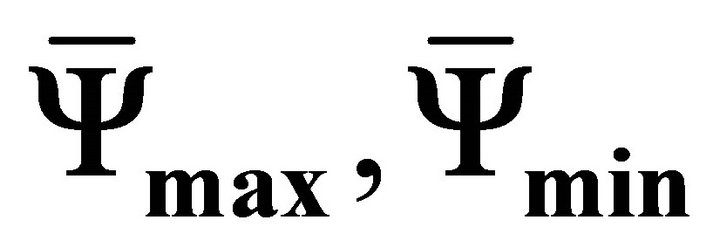 and
and

Based on a set of preliminary tests, the time-averaged values of the stream functions and the Nusselt number (Ymax, Ymin, and Nu), obtained for various periods, let suppose the existence of the resonance phenomenon within the cavity. This phenomenon is characterized by maximum fluctuations in the response of the system to an external excitation with well-defined period. This effect was reported in the past by several authors, both in the absence of radiation effect [11-21] and in the presence of radiation [22]. Hence, variations of  and
and  are presented versus t for both considered heating modes and various values of e. The values corresponding to the case of the isothermal heating sources are also presented in the same figures as references.
are presented versus t for both considered heating modes and various values of e. The values corresponding to the case of the isothermal heating sources are also presented in the same figures as references.
In the absence of radiation , variations of
, variations of  and
and  are presented in Figures 13-15, respectively.
are presented in Figures 13-15, respectively.
Variations of the main flow intensity,  , with t (Figure 13) show that
, with t (Figure 13) show that  increases with τ to a peak, characterizing a resonance phenomenon, for a critical value of τ, which is of 0008 for the SB mode and 0.00825 for the SV one. Such a difference between these critical periods can be attributed to the difference between the flow intensities for the two heating modes. Higher intensities of the main flow would lead to lower values of the
increases with τ to a peak, characterizing a resonance phenomenon, for a critical value of τ, which is of 0008 for the SB mode and 0.00825 for the SV one. Such a difference between these critical periods can be attributed to the difference between the flow intensities for the two heating modes. Higher intensities of the main flow would lead to lower values of the


Figure 13. Variations of  with the period τ for ε = 0 and different values of a.
with the period τ for ε = 0 and different values of a.


Figure 14. Variations of  with the period τ for ε = 0 and different values of a.
with the period τ for ε = 0 and different values of a.
resonant periods. Above this threshold, a further increase of τ leads to a continuous weakening of the flow intensity toward asymptotic values greater than those corresponding to the constant heating temperature , reached at high values of τ. By increasing the amplitude a of the variable temperature, the peak becomes more important and the resonance phenomenon becomes more pronounced,
, reached at high values of τ. By increasing the amplitude a of the variable temperature, the peak becomes more important and the resonance phenomenon becomes more pronounced,
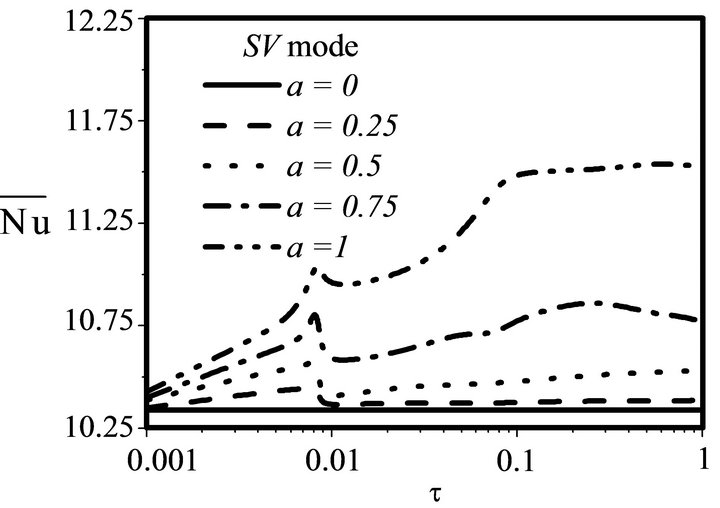
Figure 15. Variations of  with the period τ for ε = 0 and different values of a.
with the period τ for ε = 0 and different values of a.
but without changing the critical periods.
It was reported in previous studies that the resonance occurs when the time duration, necessary for the flow to rotate through the full cavity (period of a fluid wheel [11]), is equal to that of the cyclic modulated temperature. The rotational dimensional period required for a quantity of fluid to rotate along the vertical and horizontal walls in an enclosure can be expressed as [11]:

where  and
and  are the length and height of the enclosure, respectively. The scale of the characteristic velocity
are the length and height of the enclosure, respectively. The scale of the characteristic velocity  is determined by Lage and Bejan [11].
is determined by Lage and Bejan [11].
For the secondary flow, Figure 14 also shows a resonance phenomenon in the evolution of  which is well marked and premature for the SB mode with almost the same critical period observed in the evolution of
which is well marked and premature for the SB mode with almost the same critical period observed in the evolution of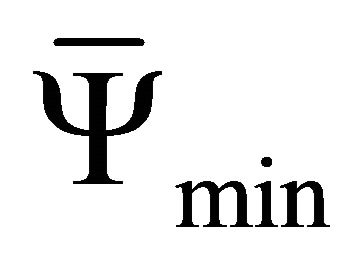 , while for the SV mode, the occurrence of this resonance is delayed and depends on the amplitude a. Beyond the critical period,
, while for the SV mode, the occurrence of this resonance is delayed and depends on the amplitude a. Beyond the critical period,  decreases and stabilizes at values depending on the heating mode considered.
decreases and stabilizes at values depending on the heating mode considered.
Regarding variations of 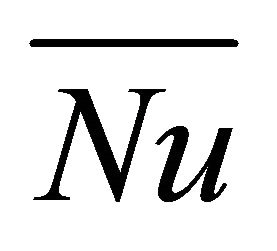 with t (Figure 15), the resonance phenomenon is also observed and appears to be more important in the case of SB mode, with critical periods identical to those on
with t (Figure 15), the resonance phenomenon is also observed and appears to be more important in the case of SB mode, with critical periods identical to those on  (0.008 for the SB mode and 0.00825 for the SV one). The later values are not affected by the increase of the oscillating amplitude a, a result in accordance with previous numerical findings [22]. Also, it is important to note that beyond the critical value of t,
(0.008 for the SB mode and 0.00825 for the SV one). The later values are not affected by the increase of the oscillating amplitude a, a result in accordance with previous numerical findings [22]. Also, it is important to note that beyond the critical value of t, 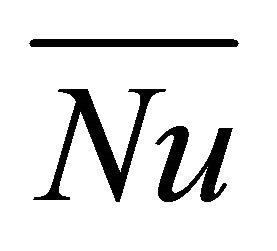 decreases to a minimum value reached for t0 which depends on the heating mode imposed. In the case of SB mode,
decreases to a minimum value reached for t0 which depends on the heating mode imposed. In the case of SB mode,  , while in the case of the SV one, t0 is substantially less and is 0.01, values beyond which
, while in the case of the SV one, t0 is substantially less and is 0.01, values beyond which  increases until an asymptotic trend, depending on a.
increases until an asymptotic trend, depending on a.
In the case of highly emissive walls , Figures 16-18 show that the fluid circulation and the total heat transfer are more enhanced in comparison with the case of e = 0. When e passes from 0 to 1, the enhancement of
, Figures 16-18 show that the fluid circulation and the total heat transfer are more enhanced in comparison with the case of e = 0. When e passes from 0 to 1, the enhancement of


Figure 16. Variations of  with the period τ for ε = 1 and different values of a.
with the period τ for ε = 1 and different values of a.


Figure 17. Variations of  with the period τ for ε = 1 and different values of a.
with the period τ for ε = 1 and different values of a.
the time averaged heat transfer,  , is of about 142% at the resonance.
, is of about 142% at the resonance.
The evolutions with τ are similar to those obtained without radiation effect. The resonance phenomenon is obtained for the same critical periods for both considered heating modes.
The contribution of radiation to total heat transfer


Figure 18. Variations of  with the period τ for ε = 1 and different values of a.
with the period τ for ε = 1 and different values of a.
through the cavity is also examined in this study for the two considered configurations, SB and SV heating modes. The obtained results show that for a moderate value of the emissivity , the contribution of radiation is not negligible and it is close to that obtained for the steady state case (a = 0). Note that in the case of the SV mode, an increase of a leads to a decrease in the contribution of radiation. In the SB heating mode, this decrease occurs specifically for high values of t. For e = 1, a higher contribution of radiation to total heat transfer is obtained (between 59% and 62%) when compared to that of natural convection.
, the contribution of radiation is not negligible and it is close to that obtained for the steady state case (a = 0). Note that in the case of the SV mode, an increase of a leads to a decrease in the contribution of radiation. In the SB heating mode, this decrease occurs specifically for high values of t. For e = 1, a higher contribution of radiation to total heat transfer is obtained (between 59% and 62%) when compared to that of natural convection.
5. Conclusion
The problem of natural convection coupled with thermal radiation inside a square cavity, submitted to cross gradients of temperature, is studied numerically. Two different heating modes (SB and SV), with a periodic variation in time, are considered. In such a situation, the solutions obtained with and without thermal radiation, are periodic in time with periods identical to that of the exciting temperature. A resonance phenomenon, characterized by maximum fluctuations of the flow intensity and heat transfer rate, is observed. The resonance period of SB mode is slightly lower than that of SV one. Both these periods have the particularity of being independent on the excitation amplitude and the walls emissivity. Except for low values of the excitation period, time variable heating improves, generally, heat transfer than constant heating, which makes the former interesting for the heat removal through the cavity. Moreover, the control of the coupling convection-radiation, in the unsteady regime, appears to be a good means to control heat transfer for very specific values of the governing parameters.
Nomenclature
Ar: aspect ratio of the cavity 
B: relative lengths of the active portions,

cv: convection Fij: view factor from Si surface to Sj one
g: acceleration due to gravity, 
 : length of the vertical active portions, m
: length of the vertical active portions, m
 : height of the cavity, m Ji: dimensionless radiosity,
: height of the cavity, m Ji: dimensionless radiosity, 
 : width of the horizontal active elements, m
: width of the horizontal active elements, m
 : length of the cavity, m Nr: convection-radiation interaction parameter,
: length of the cavity, m Nr: convection-radiation interaction parameter,
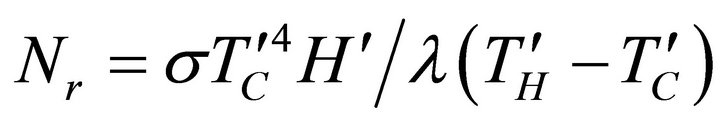
Nu: average Nusselt number Pr: Prandtl number, 
Qr: dimensionless radiative heat flux, 
Ra: Rayleigh number, 
rd: radiation t: dimensionless time, 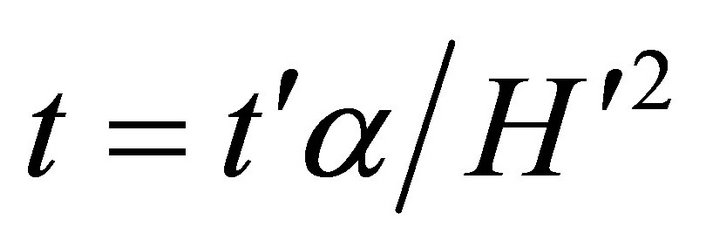
 : dimensional fluid temperature, K T: dimensionless fluid temperature,
: dimensional fluid temperature, K T: dimensionless fluid temperature,

 : temperature of the cold elements, K
: temperature of the cold elements, K
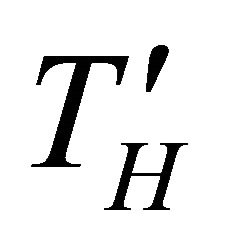 : temperature of the heated elements, K
: temperature of the heated elements, K
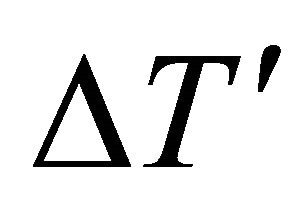 : temperature difference,
: temperature difference, 
Tr: dimensionless reference temperature,
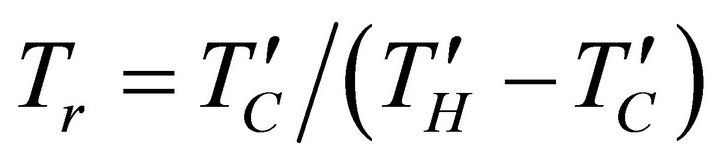
 : dimensionless horizontal and vertical velocities,
: dimensionless horizontal and vertical velocities, 
 : dimensionless coordinates,
: dimensionless coordinates, 
Greek Symbols
 : thermal diffusivity of fluid,
: thermal diffusivity of fluid, 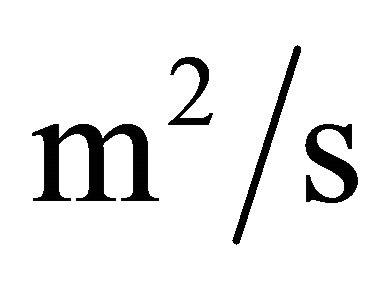
 : thermal expansion coefficient of fluid,
: thermal expansion coefficient of fluid, 
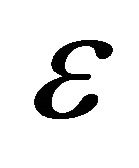 : emissivity of the walls
: emissivity of the walls
 : thermal conductivity of fluid,
: thermal conductivity of fluid, 
n: kinematic viscosity of fluid, 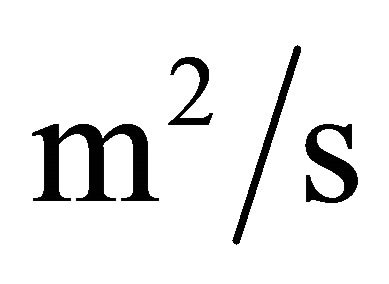
t: dimensionless period of the heating temperature, 
 : dimensionless vorticity,
: dimensionless vorticity, 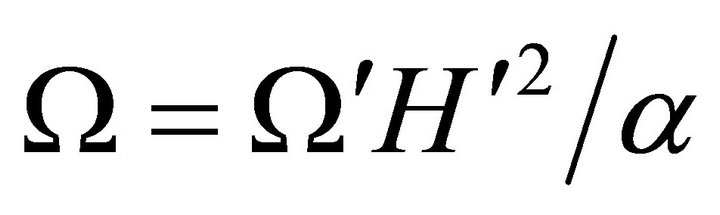
 : dimensionless stream function,
: dimensionless stream function, 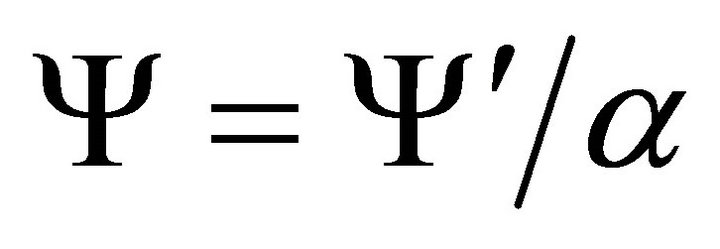
 : Stéfan-Boltzman constant,
: Stéfan-Boltzman constant,

Subscripts
C: cooled surface H: heated surface
Superscripts
¢: dimensional variable