1. Introduction
When
is a commutative graded algebra with unit
over a commutative field
with characteristic zero, a
-linear map
is a first order differential operator and of degree r (
), if
fulfills
(1)
for homogeneous elements
, where
denotes the degree of
. Let
be a first order differential operator and of degree r, let
be another first order differential operator and of degree
, then the bracket
such that
(2)
is a first order differential operator and of degree
.
Thus the pair
is a differential algebra if
is a commutative graded algebra with unit
and
is a first order differential operator and of degree +1 such that
.
We consider a commutative algebra
with unit
over a commutative field
with characteristic zero.
We denote
an
-module. For any
,
denotes the multiplication by
.
The set,
, of all first order differential operators from
into
is an
-module and admits a
-Lie algebra structure.
We denote,
, the set of
-derivations from
into
which is an
-submodule and a
-Lie subalgebra of
The main goal of this paper is to study some properties of first order differential operators from an algebraic viewpoint and geometric viewpoint. We also give an example of these applications in the last case at a point and we construct the basis of the set of all these maps and its dual basis.
2. Differential Operators from
into
A differential operator of order
, from
into
is a
-linear map
such that for any
, the map
is a differential operator of order
from
into
.
A differential operator of order zero is an
-linear map from
into
.
Proposition 1 A
-linear map
is a first order differential operator from
into
if and only if
(3)
for all a and b elements of
.
Proof. Assume that
is a first order differential operator from
into
, then for any
, the map
is
-linear. Thus for any
,
. Therefore we have the following
We deduce that
Conversely if
for any
, then we obtain
That ends the proof.
For any
, we can easily see that the map
is a first order differential operator from
into
.
Proposition 2 [1] The
-linear map D from
into
is a first order differential operator if and only if the map
is a derivation.
Proof. As D is a first order differential operator from
into
, for any
, we verify that
Conversely, let
be a derivation, then by straightforward calculation do that D is a first order differential operator.
Theorem 3 The map
is an isomorphism of
-modules.
Proof. The map
is
-linear.
For any
, the map
is
-linear and is a first order differential operator. Indeed for any
,
Then
We also verify that the map
is
-linear. For any pair
and for
We deduce that
and
Thus
We have
So
for any
and
.
And
So
.
Thus the map
is an isomorphism of
-modules.
In the following, we shall consider the
-module
where
is the
-module of Kähler
-differential of
and
is the canonical derivation [1] [2] [3] and the term differential operator will mean first order differential operator.
Theorem 4 [1] [3] The map
is a differential operator and the image of
generates the
-module
. Furthermore the pair
possesses the following universal property: for any
-module
and for any differential operator
then there exists one and only one
-linear map
such that
(4)
The map
is an isomorphism of
-modules [1] [3].
We recall that an alternating p-differential operator from
into
is an alternating
-multilinear map
such that for all p elements
, the map
is a differential operator for any
.
Theorem 5 [1] Let
be an alternating p-differential operator, then there exists an unique alternating
-multilinear map
such that
(5)
for all
.
We note
, the p-exterior power of the
-module
.
Theorem 6 [1] The map
is a p-alternating differential operator and the image of
generates the
-module
. Moreover, the pair
possesses the following universal property: for any
-module
and for any alternating p-differential operator
there exists an unique
-linear map
such that
(6)
We deduce that
is an isomorphism of
-modules.
Let
be the exterior
-algebra of
-module
[3].
Theorem 7 The differential operator
extends along a differential operator, denoted once again
, from
into
of degree +1 and of square zero such that the pair
is the differential algebra in the sense of Okassa [1].
Proposition 8 For any integer p
, the map
is alternating
-multilinear and induces an
-linear map
which extends along an
-endomorphism of
, noticed once again
, of degree −1.
Theorem 9 For any
, the inner product
satisfies
(7)
for all
and where
denotes the degree of
. Moreover, the bracket
is a differential operator of
and of degree zero.
Proof. It is obvious.
Proposition 10 For any
, we get
(8)
Proof. As
and
, then we have
That ends the proof.
Theorem 11 For all
and
, we have
(9)
(10)
and
(11)
Proof. The result is immediate.
3. Applications in Geometry
In what follows, M denotes a paracompact and connected smooth manifold,
the algebra of numerical functions of class
on
the
-module of vector fields on
the unit of
the
-module of differential operators on
and
the cohomology operator associated with the identity map
3.1. Differential Operators of
We recall that if
is the usual Lie bracket on
then for all
and
, we have
(12)
In particular
(13)
(14)
(15)
Proposition 12 [1] [4] [5] When
and
are two differential operators of
, with f and g elements of
, X and Y elements of
, then the bracket on
is given by
(16)
Proof. By straightforward calculation, one has
That ends the proof.
Let
be a smooth manifold and let
be a differential map.
The map
is an homomorphism of real algebras.
If
is a diffeomorphism and
its inverse, then
is an isomorphism of real algebras such that
(17)
Proposition 13 If f is a diffeomorphism and D is a differential operator of
, then the map
is a differential operator of
called image of
by f.
Theorem 14 Let
be two differential operators of
, if f is a diffeomorphism, then
(18)
Proof. Indeed, we verify that
That ends the proof.
Proposition 15 Let D be a differential operator, when f is a diffeomorphism then for any g element of
, we have
(19)
Proof. Let
, we have
We deduce that
.
Proposition 16 When f is a diffeomorphism and
be a multilinear p-form on
, for all
differential operators of
, we have
(20)
Theorem 17 If f is a diffeomorphism then
and
commute.
Proof. We have
On the other hand, we get
That ends the proof.
3.2. Differential Operators of
Let
be the algebra of smooth functions defined in the neighborhood of
the unit of
.
A differential operator at
is a linear map
such that
 (21)
(21)
for all functions f and g in .
.
Example 18 The Dirac mass at ,
,

is a differential operator at p.
We verify that the set, 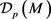 , of differential operators at p is a real vector space and the map
, of differential operators at p is a real vector space and the map

is an isomorphism of vector spaces. Moreover, for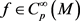 , the map
, the map

is a linear form on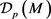 .
.
Theorem 19 Let U be an open neighborhood of p in M of coordinate functions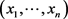 , then
, then 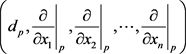 is the basis of
is the basis of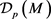 . The system
. The system
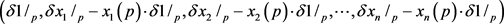 (22)
(22)
is the dual basis of the basis of  and
and
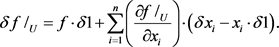 (23)
(23)
Conclusion 20 In this paper, after having given the definition of differential operator by a relation of recurrence, one decomposes it and one states some properties from the algebraic viewpoint. We define the Lie derivative with respect to a differential operator. From a geometric viewpoint, some properties on the algebra of smooth functions were given. The Dirac mass at a point was the best example of differential operators at this point.