1. Introduction
Article [1] introduced the T3 tree and showed a number of properties of tree, including divisibility, multiples and divisors and multiplications of the nodes. Looking through the other papers that are related with the article [1] , such as articles [2] - [7] , one can see that the T3 tree is really a new attempt to study integers. However, one can also see that, there has not been an article that concerns the square root of a node in the T3 tree. As is known, a divisor of integer N must be no bigger than
. Hence the location where
lies in the T3 tree is important for finding N’s divisor. Accordingly, this article makes an investigation on the issue and presents the results.
2. Preliminaries
2.1. Symbols and Notations
Symbol T3 is the T3 tree that was introduced in [1] and [2] and symbol
is by default the node at position j on level k of T3, where
and
. An integer X is said to be clamped on level k of T3 if 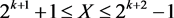 and symbol
indicates X is clamped on level k. An odd interval
is a set of consecutive odd numbers that take a as lower bound and b as upper bound, for example,
. Intervals in this whole article are by default the odd ones unless particularly mentioned. Symbol
is the floor function, an integer function of real number x that satisfies inequality
, or equivalently
and symbol
indicates X is clamped on level k. An odd interval
is a set of consecutive odd numbers that take a as lower bound and b as upper bound, for example,
. Intervals in this whole article are by default the odd ones unless particularly mentioned. Symbol
is the floor function, an integer function of real number x that satisfies inequality
, or equivalently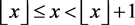 . Symbol
means conclusion B can be derived from condition A.
. Symbol
means conclusion B can be derived from condition A.
2.2. Lemmas
Lemma 1 (See in [1] ). Let
be the node at the jth position on the kth level of T3 with
and
; then
.
Lemma 2 (See in [8] ). For real numbers x and y, it holds
(P2) 
(P8)
with n being a positive integer
(P13) 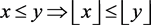
(P17)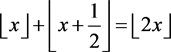 ,
,
3. Main Results and Proofs
Theorem 1. Let
be an integer and
be a real number; then it holds
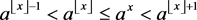 (1)
(1)
and
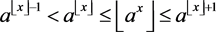 (2)
(2)
Proof. Since
, the definition 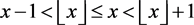 immediately yields
immediately yields
Since a and 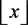 are integers, it yields by Lemma 2 (P13)
are integers, it yields by Lemma 2 (P13)
Considering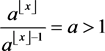 , it knows
; consequently
, it knows
; consequently
Theorem 1. Let n be a positive integer and
then
,
(3)
Proof. 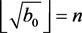 and
obviously hold. Now consider that, for
, it holds
and
obviously hold. Now consider that, for
, it holds
This is to say that,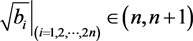 ; since n is an integer, it is sure by definition of the floor function
; since n is an integer, it is sure by definition of the floor function
Corollary 1. Let n and
be a positive integers and
then
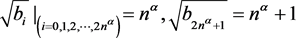 (4)
(4)
Proof. (Omitted)
Example 1. Take
,
; then
.
Theorem 2. Let n and
be a positive integers and
then
Proof. See the following deductions.
1) 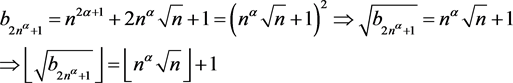
2) By Lemma 2(P13)
Example 2. Take 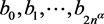 and
by
and
by
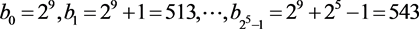 ,
,
then
,
,
then
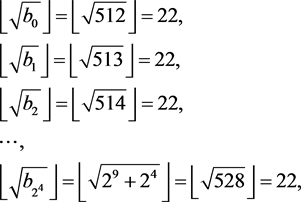
Theorem 4 Suppose integer k satisfies
and
be the leftmost node on level k of T3; then  is even if k is odd, whereas, it can be either odd or even if k is even.
is even if k is odd, whereas, it can be either odd or even if k is even.
Proof. Since
, it knows by Corollary 1 ![]() for an odd k. If k is even, let it be
; then by Theorem 2
or
, which indicates
can be either odd or even.
for an odd k. If k is even, let it be
; then by Theorem 2
or
, which indicates
can be either odd or even.
Example 3. Taking
and
as examples results in the following results.
Theorem 5. Suppose integers k and j satisfy
and
; let
be the node at position j on level k of T3; then it holds
![]() (5)
(5)
Proof. Since
, it yields
; hence it holds
By Lemma 2 (P13), it yields
(6)
By Theorem 1, it holds
and
Hence it results in
That is
(7)
or equivalently
(8)
Corollary 2.
is clamped in T3 on level
and or level
.
Proof. Since
the biggest node on level
and
is the smallest node on level
, it knows by (8)
may be clamped on levels from
to
, totally
levels.
By Lemma 2 (P2)
By Lemma 2 (P17 & P8)
Hence the corollary holds
Example 4. Taking the smallest nodes and the biggest nodes on level 7 and level 10 respectively, it can see that
is clamped on 2 levels, whereas
is clamped on 1 level.
4. Conclusion
Elementary number theory shows that an integer must have a divisor smaller than the square root of the integer itself. Hence the square root is undoubtedly an important issue of an integer. Since T3 tree is considered to be a new tool to study integers, the square root of a node is certainly helpful to know the distribution of the node’s divisors. The properties proved in this article are sure to provide a know-about the square root of the nodes. We hope it will be useful in the future.
Acknowledgements
The research work is supported by the State Key Laboratory of Mathematical Engineering and Advanced Computing under Open Project Program No. 2017A01, the Youth Innovative Talents Project (Natural Science) of Education Department of Guangdong Province under grant 2016KQNCX192, 2017KQNCX230. The authors sincerely present thanks to them all.