Asymptotic Analysis for U-Statistics and Its Application to Von Mises Statistics ()
1. Introduction
Consider the measurable space (
), with measure
. Let 
denote the real Hilbert space of square integrable real functions. Let 
denote the Hilbert-Schmidt operator associated with the kernel 
and defined via
Let 
be its eigenvalues. Without loss of generality we shall assume that
.
Let 
denote an orthonormal complete system of eigenfunctions of 
of the corresponding eigenvalues
. Then
(1.1)
since 
is a Hilbert-Schmidt operator and the kernel 
is degenerate. The series in (1.1) converges in 
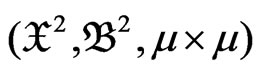. Consider the subspace 
generated by 
and eigenfunctions 
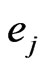corresponding to nonzero eigenvalues
. Introducing, if necessary, an eigenvalues 
,we can assume that 
is an orthonormal basis in 
. Thus, we have
in
, 
,(1.2)
with 
and
, for all j. Therefore 
is an orthonormal system of random variables with zero means.
Hilbert space 
consists of 
, such that
.
Consider the random vector
,(1.3)
which takes values in
. Since 
is a system of mean zero uncorrelated random variables with variances 1, the random vector 
has mean zero and 
and 
is Kronecker’s symbol. Using (1.1) and (1.2), we can write
, 
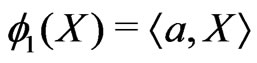, (1.4)
where we define 
for 
and
. The equalities (1.4) allow us to assume that the measurable space 
is
. Let 
be a random vector taking values in 
with mean zero and covariance 
and that
,
. (1.5)
Without loss of generality we shall assume that the kernels 
and 
are linear functions in each of their arguments ([2]).
Introduce the definitions:
, 
, 
, 
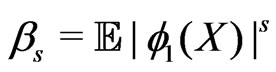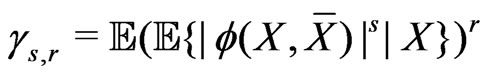and assume that
,
.
for the statistic 
we can write
.
The statistic 
is called degenerate since 
ensures that the quadratic part of the statistic is not asymptotically negligible and therefore statistic 
is not asymptotically normal. More precisely, the asymptotic distribution of 
is non-Gaussian and is given by the distribution of the random variable
,(1.6)
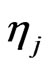is a sequence of i.i.d. standard normal variables, 
denotes a sequence of square summable weights and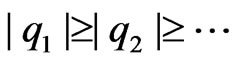 
denote eigenvalues of the Hilbert-Schmidt operator, say
, associated with the kernel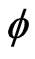
.
Consider the concentration functions of statistic 
, 
,(1.7)
where 
is an arbitrary statistic depending only on
, 
is as well arbitrary but independent of
. Note that the class of statistics 
is slightly more general than the class of statistics T. We shall denote 
constants. If a constant depends on, say s, we shall write
.
Consider the distibution functions
, 
, 
, 
,
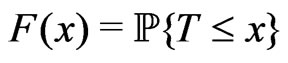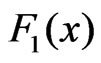denotes an Edgeworth correction.The Edgeworth correction 
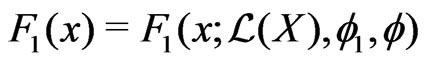is defined as a function of bounded variation satisfying 
and with the Fourier-Stieltjes transform given by
.
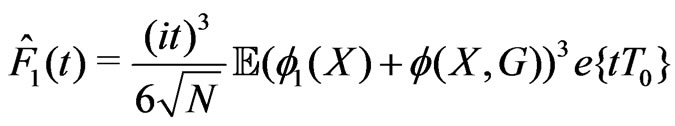Let us notice that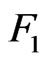 
vanishes if 
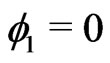or if
(1.8)
holds for all
. Using the technique presented in this work we may obtain the result for approximation bound of order 
for U-statistic distribution function which has an order 
(see Theorem 3, 2) below) or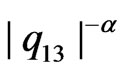 
(see Theorem 3, 1) below) with respect to dependence on first nine or thirteen eigenvalues of operator
, respectively.
2. Auxiliary Results
Consider the vector 
with values in
, where 
standard normal variables. Let us formulate lemma in which equalities for the moments of determinants of random matrices consisting of the scalar products such as 
are obtained. Analogue of this lemma is proved in [1] for matrices consisting of the scalar products such as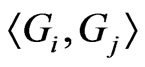 
where G-Gaussian 
vector.
Lemma 1. Let 
be random elements in a Hilbert space 
such that
, where 
standard normal variables. Let 
be the eigenvalues of Hilbert-Schmidt operator
.
, where
,
.
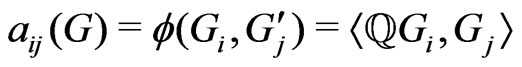Then
,
.
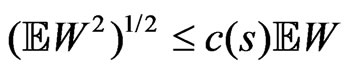Nondegeneracy condition
We shall assume that random vector
, a kernel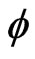
, parameters 
and 
satisfy the nondegeneracy condition if
, 
,
, 
, 
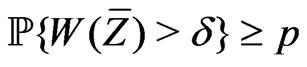,(2.1)
where
, 
, 
, 
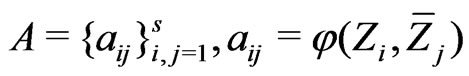are independent copies of
.
Here parameter 
is small and parameter 
is close to 1. Let 
denote the set of all vectors 
satisfying the nondegeneracy condition.
Notice that 
satisfies the nondegeneracy condition. Let vectors 
and 
have equal means and covariances, then
, 
,
,
.
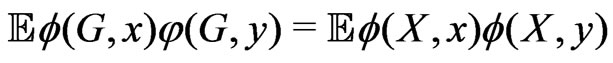The following Lemma 2 means that increase of 
yields equivalence of nondegeneracy conditions fulfillments for sum and Gaussian vector.
Lemma 2. Let 
be a Gaussian random vector and
. Then for 
we have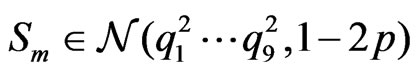
, where 
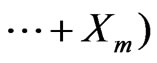is random sum.
Further, it is necessary to bound the characteristic function of the statistic
. That will be done in Lemmas 3, 4 and Theorem 1.
The following Lemma 3 has a similar proof to Lemma 6.5 from [2].
By 
we shall denote independent copies of a symmetric random variable 
with nonnegative characteristic function and such that
,
.(2.2)
Lemma 3. Let 
and
. Assume that vector 
takes values in
. Write
, 
, 
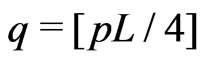where 
and 
are independent copies of Y. Then
, 
, 
where 
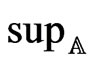denotes the supremum over all 
nonrandom matrices 
such that
.
U and V denote independent vectors in 
which are sums of n independent copies of
.
In the following lemma the bound from above for the characteristic function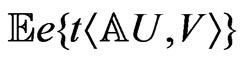 
is received. This results was proved in [1]. The received estimation contains the determinant of matrix in right-hand side of inequality. This fact allows to use eigenvalues of operator 
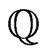for the estimation of characteristic function.
Lemma 4. Let A be a nondegenerate 
matrix. Let 
denote a random vector with covariance
. Assume that there exists a constant 
such that
, 
,
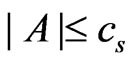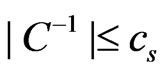.(2.3)
Let 
and 
denote independent random vectors which are sums of n independent copies of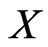
. Then
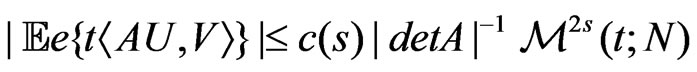for
, where 
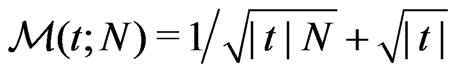for
.
Using our Lemmas 3 and 4 we may obtain a bound for characteristic function for statistic
.
Theorem 1. Let
. Assume that the sum 
. Then, for any statistic 
we have
.
The proof of this theorem is similar to proof of Theorem 6.2 in [2].
Write :
.(2.4)
In following lemma a multiplicative inequality for characteristic function of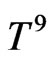 
is given. This inequality yields the desired bound 
for an integral of the characteristic function of a U-statistic. Similar result was proved in Lemma 7.1 in [2]
Lemma 5. Let 
and
. Assume that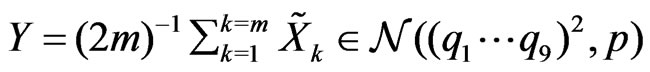 
. Then there exist constants 
and 
such that the event
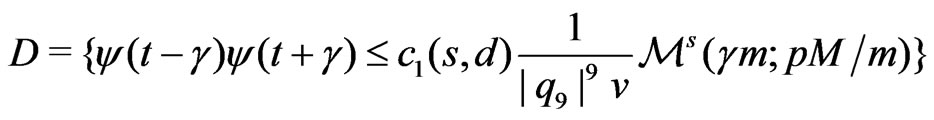,(2.5)
satisfies
.(2.6)
For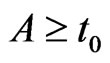
, 
define the integrals
, 
where 
denotes the Fourier-Stieltjes transform of the distribution function
. The estimation for these integrals is received in following lemma, which has a proof similar to Lemma 3.3 in [2].
Lemma 6. Let
. Assume that the random vector
and
. Let
, 
, 
, 
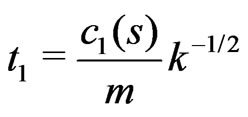where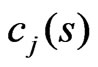
, 
are some positive constants.
Then
,
.(2.7)
3. Approximation Accuracy Estimation
For 
and functions
, introduce the statistic
(3.1)
where
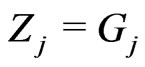for
, 
for
.
Write 
and put
,(3.2)
where
,(3.3)
,(3.4)
where supremum is taken over all linear statistics
, that is, over all functions which can be represented as 
with some functions 
.
Consider the following Lemma 7, which has a similar proof as Lemma 4.2 in [2].
Lemma 7. Let
, 
and 
. Assume that the random vector 
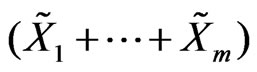satisfies the nondegeneracy condition. Then, for
, 
the distribution function 
of 
satisfies
,(3.5)
where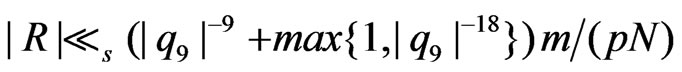
.
The Edgeworth correction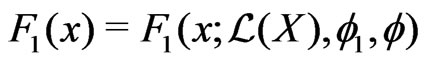 
is defined as a function of bounded variation satisfying 
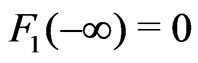and with the Fourier-Stieltjes transform given by
.(3.6)
Lemma 8. Assume that the nondegeneracy condition is fulfilled.
1) Let 
and 
. Then
(3.7)
2) Assume that the condition (1.8) holds and that
. Then
(3.8)
To prove this lemma we need to make the same steps as in Lemma 4.1 in [2] replacing Theorem 6.2 by Theorem 1.
Now we can formulate a following Theorem 2, where bounds for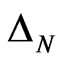 
are obtained. This theorem were proved in [4]:
Theorem 2. 1) Let 
,
. Then
(3.9)
2) Assume that (1.8) holds and
. Then
(3.10)
4. An Extension of Bounds to Von Mises Statistics. Applications
Assuming that the kernels 
and 
are degenerate, consider the von Mises statistic
.(4.1)
Introducing the function 
with
, we can rewrite (4.1) as
(4.2)
In this section we shall extend the bounds to statistics of type (4.2), assuming that 
and 
.
Similarly to the case of
, we can represent the kernel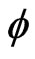 
(respectively, 
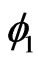and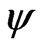
) as a bilinear (respectively, linear) function, defined on
. However in this case we have to assume that 
has an additional coordinate since 
can be linearly independent of 
and of the eigenfunctions of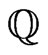
. To fix notation, we shall assume that 
consists of vectors 
. Then all representations and results of Section 2 concerning 
and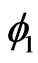 
still hold, and for 
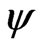we have 
with some 
such that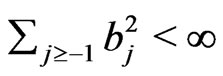
. Write
.
Introduce the function 
of bounded variation (provided that
) with the Fourier-Stieltjes transform
and such that
. Bellow we shall show that (see Lemma 9.3 [2])
.(4.3)
Notice that 
whenever
.
Write
, and let 
denote the distribution function of
. Define
,
.
Theorem 3. 1) Assume that
. Then we have
(4.4)
2) Assume that (1.8) is fulfilled and
. Then we have
Proof. We shall use the following estimates. Write
,
.(4.5)
Expanding with remainder
, splitting the sum 
in parts and conditioning , we have
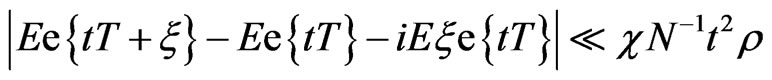.(4.6)
Proceeding similarly to the proof of Lemma 8.2 from [2], we obtain
.(4.7)
Applying the Bergstrom-type identity
,
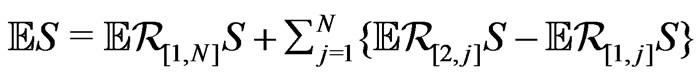with 
and proceeding similarly to the proof of Lemma 8.3 from [2], we get
(4.8)
Arguments similar to the proof of Lemma 8.5 from [2] allow proving
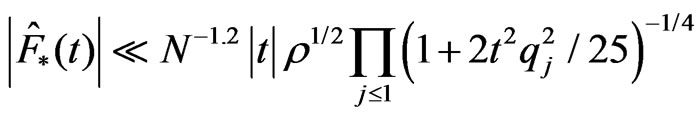,(4.9)
and, for
,
, 
(4.10)
.(4.11)
The estimates (4.6)-(4.11) allow proceeding similarly to the proof of Theorem 2, using a lemma similar to Lemma 8. Proving such a lemma, we have to apply Lemma 8 to the distribution function
. This is possible since that statistic 
is a statistic of type (3.1). The estimates (4.10) and (4.11) allow application of the Fourier inversion to the function
. As a result, we arrive at
.
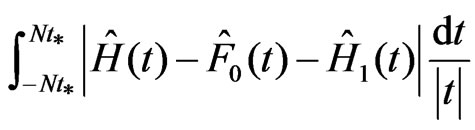Here, however, we have
, and
(4.12)
Therefore, using (4.6)-(4.8), we can proceed as in the proof of Lemma 11. As a final result we get bounds similar to those of Theorem 2, with the additional summand
.
[1] V. Ulyanov and F. Götze, “Uniform Approximations in the CLT for Balls in Euclidian Spaces,” 00-034, SFB 343, University of Bielefeld, 2000, p. 26. http://www.math.uni-bielfeld.de/sfb343/preprints/pr00034.pdf.gz
[2] V. Bentkus and F. Götze, “Optimal Bounds in NonGaussian Limit Theorems for U-Statistics,” The Annals of Probability, Vol. 27, No.1, 1999, pp. 454-521. doi:10.1214/aop/1022677269
[3] S. A. Bogatyrev, F. Götze and V. V. Ulyanov, “NonUniform Bounds for Short Asymptotic Expansions in the CLT for Balls in a Hilbert Space,” Journal of Multivariate Analysis, Vol. 97, 2006, pp. 2041-2056.
[4] T. A. Zubayraev, “Asymptotic Analysis for U-Statistics: Approximation Accuracy Estimation,” Publications of Junior Scientists of Faculty of Computational Mathematics and Cybernetics, Moscow State University, Vol. 7, 2010, pp. 99-108. http://smu.cs.msu.su/conferences/sbornik7/smu-sbornik-7.pdf