SIR Model of Spread of Zika Virus Infections: ZIKV Linked to Microcephaly Simulations ()
1. Introduction
1.1. Historical Background
On February 1st, 2016, the World Health Organization declared ZIKV epidemic in the Americas as a Public Health Emergency of International Concern. The foremost reason is due to an emerging linkage with congenital birth anomalies such as microcephaly and Guillain-Barre syndrome [2] plus mode of transmission which had not known before (sexual-transmission). Since then, ZIKV is one of the most uprising viral disease in the world, especially in the Americas. Resent studies report that ZIKV is transmitted not only via mosquito bite but also via sexual contacts, blood contamination and mother-to-child-transmission [1] . The mosquito involved in the transmission is infected Aedes Aegypti. This particular mosquito belongs to the family Flaviviridae and Genus Flavivirus. Chikungunya, Dengue and Yellow fever are also the off shots of this family. Prenatal or perinatal complications of ZIKV infections have been noted due to ZIKV. There is some evidence that perinatal transmission may occur, most probably transplacental or during the delivery of a viraemic mother [3] . The virus has been detected in human saliva, semen and urine of which leads to sexual-transmission of ZIKV [4] [5] .
Despite the fact that attack of ZIKV shows moderate disease symptoms, like that of the clinical presentation and transmission cycles in the epidemiology of Chikunganya and Dengue, symptoms of ZIKV disease encompasses conjunctivitis, skin rash, fever, muscle pains in various joints, non comforting nuisance and headache, which can last normally between 2 to 7 days time period. Not limited to those, it has been found that about 80% of individuals infected by ZIKV are asymptomatic [6] [8] . In new babies, congenital microcephaly is a descriptive diagnosis. According to WHO, it is defined as a head circumference equal to or lower than two standard deviations below the mean (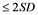 ) for age and sex or about less than the second percentile [9] . Microcephaly results from reduced brain growth. Affected infants are born with a smaller head size than normal, or their head stops growing after birth. It is a rare condition with estimated incidences varying geographically; in the United States reported incidence ranges from 2 to 12 babies per 10,000 live births. There is an association between the severity of microcephaly and that of neurological impairment [7] [10] .
) for age and sex or about less than the second percentile [9] . Microcephaly results from reduced brain growth. Affected infants are born with a smaller head size than normal, or their head stops growing after birth. It is a rare condition with estimated incidences varying geographically; in the United States reported incidence ranges from 2 to 12 babies per 10,000 live births. There is an association between the severity of microcephaly and that of neurological impairment [7] [10] .
The causes are numerous, including chromosomal abnormalities, intrauterine infections, exposure to toxic substances during pregnancy, and severe malnutrition [11] . Some countries and territories in the Americas with reported congenital syndrome associated with Zika virus infection as of July 14, 2016 (Figure 1). WHO estimates that the fetuses of one in 100 women with Zika will go on to develop microcephaly or other abnormalities [12] .
![]()
Figure 1. Reported microcephaly associated with ZIKV infection as of July 14, 2016. PAHO.
No specific antiviral medication is available for ZIKV disease. Treatment is generally supportive and can include rest, fluids, and use of analgesics and antipyretics. Aspirin including other nonsteroidal anti-inflammatory drugs should be avoided until dengue can be ruled out to reduce the risk of hemorrhage. Febrile pregnant women should be treated with acetaminophen. Persons infected with ZIKV, dengue, or Chikungunya virus should be protected from further mosquito exposure during the first few days of illness to reduce the risk for local transmission [6] .
The very first incidence of ZIKV was identified in 1947 from species of monkey in the African forest called Zika from Uganda. And the first isolated case identified from humans in 1952 also from Uganda and then later from a neighbor country, the United Republic of Tanzania. However, comprehensive genomic comparison showed different sub-classes reflecting the existence of two main lineages, one African and the other from Asia lineage [13] [15] . ZIKV has been shown intermittent disease patterns among the people of Africa and Asia. Little clinical importance was attributed to ZIKV, for the reason that only few symptomatic cases were reported in some African and Southeast Asiatic countries at the time [14] . This situation changed in 2007, when a large outbreak was registered on the Yap Island, Micronesia, caused by the Asian ZIKV lineage. Moreover, the outbreaks reported beginning this era are from the Pacific in 2007 and 2013 from French Polynesia and Yap Island (i.e. Federated States of Micronesia) [16] . There were subsequent incidents of the virus spread to other areas of the region like Cook Islands, Chile, Pacific Islands including New Caledonia, Fiji, Samoa, Solomon Islands and Vanuatu (Figure 2).
![]()
Figure 2. World Zika situation report as of April 2014, www.who.int.
ZIKV has been steadily increasing its geographical domain, ever since its initial appearance. The pace of ZIKV outbreaks as epidemic in the Americas is on rise. Similarly, the spread of this monster is reported in more regions of the world that were previously completely unaffected, that includes Europe [18] . The immunity of Europeans population is relatively immature as contrast to Afro-Asian Populations. At the arrival of summer season in the northern hemisphere is the most suitable time when Aedes mosquitoes in Europe find optimum climate to get infected by ZIKV and later transmit this virus to tourists and then into local population through biting [17] . At this point, it is relevant to cover and analyze the monthly traffic of travelers by air, arriving into the cities of Europe from the Zika affected regions of both the American continents and Europe.
Brazil’s first confirmed Zika infection was in March 2015. Over five years preceding 2015, the country saw between 130 and 170 cases of microcephaly each year [20] . In the first nine months of 2015, this figure roughly doubled. By the end of 2015, over 2400 further similar cases had been reported [19] . Up to February 27, 2016 according to the Brazilian Ministry of Health, 5640 cases of microcephaly in the country have been reported, and 583 of them are confirmed to have microcephaly and/or other central nervous system findings, suggesting of congenital infection. Out of the total cases with confirmed microcephaly, only 67 fulfill the laboratory criteria for ZIKV infection, and 4107 across Brazil remain under investigation [14] .
Regarding general ZIKV infections, data announced on December 2015, by the ECDC estimate that between 440,000 and 1.3 million cases by autochthonous transmission of ZIKV have occurred in Brazil (Figure 3), but these data are largely underestimated and the real magnitude of the Brazilian ZIKV epidemic may be much higher [14] . As of June 2016, around 500,000 Zika virus disease (ZVD) cases have been estimated in Brazil, and autochthonous circulation has been observed in 40 countries from the Americas [8] .
1.2. Mathematical Background
Basing on the nature of epidemic, though with a relatively long history since its knowledge in 1947, few researches have been conducted. Probably, the main reason is that its effects where not vividly clear to human being as of now. However, this does not rule out that in the past people had not been affected by the problem. About three years ago, a number of researches have been working to explore the disease down so as to come up with some means to control it. According to Rojas DP et al. [8] all age groups are vulnerable, but the most affected age group is 20 to 49 years of age. A similar study previously published outbreaks in Yap Island, Micronesia, and in Salvador, Brazil [21] . As the population was fully susceptible to ZIKV transmission before the outbreaks, it is expected that all age groups would be affected. Joacim Rocklov et al. [2] , studied which seasons in the year are more risk for ZIKV transmission. There are as well
![]()
Figure 3. Zika situation report in Brazil as of April 2016 (www.who.int).
more researches in medicine and other discipline. This paper is more concerned with mathematical models exploring the epidemic. One of the model was done by Adam J. Kucharski et al. in early 2016 [22] . The model provided understanding ZVD in mathematical perspective, basing on some assumptions the model did not include sexual transmission. Khalid et al. in the late of 2016, have formulated the mathematical model by including sexual transmission [23] . One side this article is an improvement of Kucharski’s model modified to include sexual-transmission. However, not only the later but also infections to newborns through MTCT. Therefore, the model is a simple SIR model that includes newborn as part of the infected class.
2. Model Formulation
The model consists of two categories, the humans and mosquitoes with total population  and
and 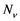 respectively. Presumably, the humans have three classes, the susceptible (S), infectious (I) and removed (R). An individual potential for infection is considered as susceptible class member, individuals who are exposed or already brown with ZIKV symptoms are classified as infectious, and individuals who have recovered from the disease are considered as removed. Exposed and fully brown ZIKV individuals are placed together because all of them can transmit the virus. It is assumed that individuals after recovery build immune against the ZIKV infection. Mosquitoes have only susceptible (
respectively. Presumably, the humans have three classes, the susceptible (S), infectious (I) and removed (R). An individual potential for infection is considered as susceptible class member, individuals who are exposed or already brown with ZIKV symptoms are classified as infectious, and individuals who have recovered from the disease are considered as removed. Exposed and fully brown ZIKV individuals are placed together because all of them can transmit the virus. It is assumed that individuals after recovery build immune against the ZIKV infection. Mosquitoes have only susceptible (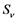 ) and infectious (
) and infectious (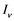 ) class. The reason is that the life span of mosquitoes is short enough to ignore the recovery period.
) class. The reason is that the life span of mosquitoes is short enough to ignore the recovery period.
Susceptible individual moves into the infectious class after effective interaction with infected mosquitoes, or sexual contact with and individual in the infectious class. Newborns with ZIKV infection by MTCT enters infected class. The mosquitoes moves from the susceptible to their infectious-class after effective infection through biting an infectious human.
In this context, in all cases the subscript  signifies a transmission vector, the mosquitoes. System (1) and Figure 4 is the model and its compartments, where as Table 1 is definitions of parameters.
signifies a transmission vector, the mosquitoes. System (1) and Figure 4 is the model and its compartments, where as Table 1 is definitions of parameters.
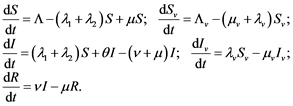 (1)
(1)
![]()
Figure 4. Model compartments flow diagram.
![]()
Assign ![]() then the system (1) may be considered as model (2).
then the system (1) may be considered as model (2).
![]() (2)
(2)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are initial values notations.
, are initial values notations.
3. The Basic Reproduction Number (![]() )
)
Consider to evaluate the basic reproduction number, ![]() from next generation method. Recall model (2), and assign roman numeral to every equation as:
from next generation method. Recall model (2), and assign roman numeral to every equation as:
![]() (3)
(3)
![]() be the disease free equilibrium point of the model, of which
be the disease free equilibrium point of the model, of which ![]() and
and![]() . On the other hand, at disease free equilibrium point, the model (3) is reduced to
. On the other hand, at disease free equilibrium point, the model (3) is reduced to
![]()
Equations i and iv are solved simultaneously, so that ![]() and
and![]() . So that the disease free equilibrium point,
. So that the disease free equilibrium point, ![]() is given by
is given by
![]() (4)
(4)
From the system of Equation (3), ![]() ,
,![]() . Thus, model (3) can be written as:
. Thus, model (3) can be written as:
![]()
![]()
Summary of infection rates, gains or losses in classes ![]() and
and![]() : gains in
: gains in![]() ; losses from
; losses from![]() ; gains in
; gains in![]() ; and losses from
; and losses from![]() . Therefore, the gain-terms matrix,
. Therefore, the gain-terms matrix,![]() :
:
![]()
The loss-terms matrix,![]() :
:
![]()
![]()
Calculations for ![]()
![]()
The eigenvalues, ![]() of
of ![]() is given:
is given: ![]() .
.![]() , since
, since ![]() takes the dominant eigenvalue of
takes the dominant eigenvalue of![]() . Therefore, the basic reproduction number,
. Therefore, the basic reproduction number,
![]() .
.
4. Stability of the Equilibrium Points
4.1. The Endemic Equilibrium Point of the Model
For endemic equilibrium, ![]() ,
,![]() . The system of Equation (3) reduces to
. The system of Equation (3) reduces to
![]() Solving this simultaneously, the equilibrium point is:
Solving this simultaneously, the equilibrium point is:![]() (5)
(5)![]() is obtained from the equation:
is obtained from the equation:![]() (6)
(6)![]() The equilibrium point reduces to a disease free when
The equilibrium point reduces to a disease free when![]() .
.![]() 4.1.1. Existence of the Endemic EquilibriumConsider Equation (6):
4.1.1. Existence of the Endemic EquilibriumConsider Equation (6):![]() . Assign
. Assign![]() . Endemic equilibrium exists whenever there is a positive solution (i.e. value of
. Endemic equilibrium exists whenever there is a positive solution (i.e. value of![]() ). When
). When![]() ,
,![]() .When
.When![]() ,
,![]() . Therefore at some point in the interval
. Therefore at some point in the interval ![]() there exists
there exists![]() , which proves the existence of endemic equilibrium. As an example, consider a simulation: Choose any
, which proves the existence of endemic equilibrium. As an example, consider a simulation: Choose any![]() ; say
; say
![]()
Figure 5. One case illustrating existence of ![]() as a solution of
as a solution of![]() , point P(1, 1).
, point P(1, 1).
![]() . Then
. Then![]() . That is, the value for
. That is, the value for ![]() is
is ![]() (Figure 5).
(Figure 5).
4.1.2. The Positivity and Boundedness of the Model Solution
By definition, the lower boundaries of the population are zero. Yet, the upper bounds can be deduced from the given dynamical equations. As it is for
![]() , from the fact that
, from the fact that ![]()
![]()
That is![]() , that
, that![]() .
.
Therefore,![]()
![]() .
.
A similar approach is used to show that![]() , where
, where ![]() is the initial population.
is the initial population.
4.1.3. Local Stability of the Disease free Equilibrium Point of the Model
In order to understand the local stability of the model, Jacobian matrix, ![]() is determined from the model (2) and used to study the local stability of the equilibrium point. Jacobian matrix,
is determined from the model (2) and used to study the local stability of the equilibrium point. Jacobian matrix, ![]() is given as
is given as
![]()
Recall the disease free equilibrium (4), ![]() . At this point, Jacobian matrix,
. At this point, Jacobian matrix, ![]() is
is
![]()
The characteristic equation, ![]()
![]()
That is![]()
![]() ,
, ![]() If
If![]() , then
, then![]() ,
, ![]() ,
,![]() . That means there is stable equilibrium if
. That means there is stable equilibrium if ![]()
![]()
![]() . It can be deduced that disease free equilibrium is stable in this case if
. It can be deduced that disease free equilibrium is stable in this case if![]() .
.
Proof: Recall that:![]() .
.
![]()
![]()
![]() or
or![]() . For
. For ![]() means there is no mosquito transmission at all, then
means there is no mosquito transmission at all, then ![]() .
.
For![]() , that is:
, that is:
![]()
Choose![]() :
:
![]()
Which suggests that ![]() is numerically less than unit, this completes the proof.
is numerically less than unit, this completes the proof.
On the other hand when ![]() the disease free equilibrium is unstable. Now that suppose
the disease free equilibrium is unstable. Now that suppose![]() , and assign
, and assign![]() .
.
![]()
The characteristic equation is Hurwitz provided that ![]()
![]()
![]() and
and![]() . Thus suggesting that
. Thus suggesting that ![]() is bifurcation point.
is bifurcation point.
5. Estimation of ZIKV Infected Newborns (M)
In the system of Equation (8), ![]() is coupled with model (2), the mission
is coupled with model (2), the mission
is to estimate the number of newborns who have been infected with ZIKV since beginning of the epidemic in a given community. The assumption is that the rate of infections (![]() ) is constant. Newborns are dying but this is not considered because the estimation is total number of infected newborns.
) is constant. Newborns are dying but this is not considered because the estimation is total number of infected newborns.
![]() (7)
(7)
order to estimate the number of infected newborns (![]() ), the differential equation
), the differential equation ![]() has been evaluated by simulation in section 6.1.1.
has been evaluated by simulation in section 6.1.1.
6. Model Simulations
There are a approximations and assumptions for estimating parameters that have been used to simulate the model. Due to inaccessibility of some parameters, assumptions have been made for some in order to fit the model with current trend of epidemic. For the purpose of simulation in the Americas, Brazil is considered as illustrative example. Model is suggesting possible outcomes but also is providing us with the virtual of ZIKV disease features. Table 2 and Table 3 are respectively list of parameter values and initial populations estimations for Brazil in 2016.
![]()
Table 2. Estimations of parameter values and their sources for year 2016.
![]()
Table 3. Values of Initial populations for model simulation as of Jan 2016 in Brazil.
6.1. Fitting the Model into Brazil ZIKV Infections State
The graphs in Figure 6 depict the dynamics of ZIKV for the first 10 years in Brazil starting June 2016. The graphs for I and R classes are not clearly seen in Figure 6(a), therefore can be seen in Figure 6(b). Although initial number individuals in a recovery class may be lower than infectious class (Figure 6(b)), but the prevalence of recovery class grows faster than the infected class. In the later time of the epidemic there more individuals in the recovery than infectious class.
Simulation of ZIKV Infected Newborns
For M estimations, the differential equation ![]() from the model (8) is
from the model (8) is
simulated for 25 months (Figure 7). In this case the objective is to estimate the
![]()
Figure 6. Graphs to estimate ZIKV situation for the next 10 years starting June 2016. (a) Graphs of populations (S, I, R) growth; (b) Growth of infected (I) and recovery (R) class.
![]()
Figure 7. Graphical simulation of ZIKV infected newborns starting January 2016 in months. (a) Plot of M; (b) Plots of I, R, and M.
total number of children who has been inflicted by ZIKV. It is clear that this accounts for all children including the initial amount as of January 2016. Up to February 27, 2016 according to Brazilian Ministry of Health, out of all reported microcephaly cases only 67 fulfill the laboratory criteria for ZIKV infection [14] .
Then, the February 2016 cases of microcephaly is assumed to be initial value for January 2016 in this simulation. Estimation for all newborns regardless of those who die later after birth, so long as had been diagnosed with microcephaly linking to ZIKV then are part of this integral. After 25 months since January 2016, the number of ZIKV infected newborns in the same month 2017 is approximated above 2100 (Figure 7(a)) and expected to rise up about 4350 in January 2018. The plot of M is an accumulation curve (it is not prevalence), (Figure 7(a) and Figure 7(b)). The graph of M is not a straight line, but is an increasing function (Figure 7(b)).
![]() as in Figure 8(a), infectious class growth is accompanied with a silent recovery class escalation. Note that there is a great number of individuals 80% who are asymptotic to the disease [6] [8] , of which they may recover without their knowledge this is not accounted for in this case. What is considered are recovery individuals who where once diagnosed with ZIKV infection. Also the prevalence for recovery is called silent simply because generally no one cares when an individual is recovered, therefore there prevalence is unnoticed. Later the recovery class R may increasingly out number the size of population in the Infectious class I (Figure 6(b)). Whenever
as in Figure 8(a), infectious class growth is accompanied with a silent recovery class escalation. Note that there is a great number of individuals 80% who are asymptotic to the disease [6] [8] , of which they may recover without their knowledge this is not accounted for in this case. What is considered are recovery individuals who where once diagnosed with ZIKV infection. Also the prevalence for recovery is called silent simply because generally no one cares when an individual is recovered, therefore there prevalence is unnoticed. Later the recovery class R may increasingly out number the size of population in the Infectious class I (Figure 6(b)). Whenever ![]() increases which leads to increase in the infections, number of individual recovering also increases considerably maintaining the recovered population size more than the infectious class (Figure 8(b)).
increases which leads to increase in the infections, number of individual recovering also increases considerably maintaining the recovered population size more than the infectious class (Figure 8(b)).
6.2. Natural Resistance Against ZIKV Epidemics
At the latest, if the situation is not attended or interrupted, naturally may lead to
![]()
Figure 8. Later the prevalence of Recovered class out sizes infected class. (a)![]() ; (b)
; (b)![]() .
.
![]()
Figure 9. Recovered class creates a silent resistant to the epidemic. (a) Recovered gets higher in zize than infected class; (b) Possible endemic equilibrium point to be reached.
equilibrium as in Figure 9. The recovered class has two important roles in suppressing the epidemic. One is that the recovered individuals build up immune against ZIKV infection. The other reason is that since the higher density of recovered individuals is in the most affected regions, this minimizes interactions between susceptible and infectious, therefore reducing spread of the epidemic. So when more individuals are recovered compared to infectious (Figure 9(a)), natural resistance is strengthened. This may save to take the endemic equilibrium point of the epidemic at a state where there is very few infectious of ZIKV for long time. This may explain a situation in the countries with historic start of ZIKV like Africa and Asia, particularly in Uganda and Tanzania. In such regions occasionally, new born with microcephaly may happen and is likely to be ignored so long as there is no substantial outbreak of the epidemic. Basing on the model simulation such a situation is reach around one generation time since start of the epidemic.
Among other reasons that can lead to microcephaly situation side track the societies attention to ZIKV disease outbreak especially when the infections are low and unnoticeable is not keeping records, especially in most villages of the developing countries. Therefore, appreciation should be given to the Americas, like Brazil for keeping records of microcephaly born children which is one of the reasons lead to notice the break of epidemic [20] .
6.3. Intervention for Epidemic Elimination
According to the model (2), two main factors to be controlled in order to diminish or eliminate the epidemic basing on the model include reducing both unsafe sexual-interaction and mosquitoes bites against humans. Controlling the two factors to the extent that ![]() such as
such as ![]() may avert the growing epidemic to one dying (Figure 10(a)).
may avert the growing epidemic to one dying (Figure 10(a)).
![]()
Figure 10. ![]() leads to free the society from Epidemic in 15 years. (a) The epidemic dies off; (b) The total population gets free of the epidemic.
leads to free the society from Epidemic in 15 years. (a) The epidemic dies off; (b) The total population gets free of the epidemic.
The model (2) estimates that in 15 years for ![]() the region can be free of the epidemic, thus leaving growth of susceptible class growing at its natural pace for Brazil Figure 10(b). It has been found that contribution in the spread of ZIKV infections by sexual-transmission is in low percentage compared to human-mosquito interaction [25] [26] . Therefore, effective elimination of the epidemics is basically freeing individuals from mosquitoes bites. This include getting rid off still water bodies, use of mosquito nets, insect repellents and use of insecticides to help exterminate mosquitoes cultures. Nevertheless, sexual-transmission has to be controlled as the second adverse case of transmission. That is, avoid or have safe sexual-interactions, especially with people traveling to and from infected regions. This may involve use of condoms, circumcision and all that contribute to secured sexual-interaction [26] .
the region can be free of the epidemic, thus leaving growth of susceptible class growing at its natural pace for Brazil Figure 10(b). It has been found that contribution in the spread of ZIKV infections by sexual-transmission is in low percentage compared to human-mosquito interaction [25] [26] . Therefore, effective elimination of the epidemics is basically freeing individuals from mosquitoes bites. This include getting rid off still water bodies, use of mosquito nets, insect repellents and use of insecticides to help exterminate mosquitoes cultures. Nevertheless, sexual-transmission has to be controlled as the second adverse case of transmission. That is, avoid or have safe sexual-interactions, especially with people traveling to and from infected regions. This may involve use of condoms, circumcision and all that contribute to secured sexual-interaction [26] .
As for women who want to get pregnant but are not sure of ZIKV infections (no symptoms) but they have been exposed to ZIKV infected regions or had sex with ZIKV diagnosed partners, should wait at least eight weeks after exposure. For those with diagnosed ZIKV infections, wait after eight weeks since the start of symptoms (Figure 11).
7. Conclusions
The fundamental part in the analysis of model (2) is the basic reproduction number (![]() ).
).![]() has been analyzed both analytically and at least one example numerically. An insight into the stability of disease free equilibrium point is that for some conditions it is stable if
has been analyzed both analytically and at least one example numerically. An insight into the stability of disease free equilibrium point is that for some conditions it is stable if![]() , unstable when
, unstable when![]() .
.
Model simulations have been conducted, considering Brazil as an example. However, values of the parameters have been a challenge, some range between values, some no information and others just varies. Parameters for simulation in
![]()
Figure 11. Provided by the U.S. Centers for Disease Control and Prevention (CDC).
this case have been assumed to be constant, therefore some assumptions or estimations have been done in some way to fit the current trend of the epidemic in Brazil. A population of more than 208 million as of January 2016 is found with 672,000 infected individual. Up to February 27, 2016; 67 newborns with microcephaly were confirmed to have been due to ZIKV infections. On simulations, there are at least 2100 in total of babies who have been ZIKV infected by January 2017, this number is expected to rise up about 4350 by January 2018 (Figure 7(a)). Moreover, numerically, the endemic equilibrium exist and in lower amount of infectious than recovered class, contrasting a situation in the beginning of epidemic. This suggests why most of the countries experienced ZIKV infections some past years are not easily getting erupted with the ZIKV epidemic. Among reasons behind this is that recovered class individuals not only are resistant to ZIKV infections but also reduces the interaction between infected and susceptible individuals simply by their density in the area being higher than susceptible.
The value of ![]() is simulated and found to escalate the epidemic and gets worse when
is simulated and found to escalate the epidemic and gets worse when![]() . However, when
. However, when![]() , specifically
, specifically ![]() the epidemic diminishes, it is expected that with
the epidemic diminishes, it is expected that with ![]() the elimination of epidemic is even more effective. The model suggests mainly two ways to avoid ZIKV infections. First of all, avoid mosquito bites, which is suggested that in percentage mosquito-transmission is more calling as severe than sexual-transmission. This can be done by eradicating unnecessary still water bodies, use of bed nets, mosquito repellent and insecticides. Secondly, conduct safe sexual relations especially with one who have been exposed to ZIKV infected regions, bearing in mind that 80% of ZIKV infections are asymptotic [8] . As for women who want or are preparing to get pregnant then if previously had exposed to ZIKV infected regions, having infectious symptoms or not, one is advised to wait until after 8 weeks since last exposure or start of symptoms.
the elimination of epidemic is even more effective. The model suggests mainly two ways to avoid ZIKV infections. First of all, avoid mosquito bites, which is suggested that in percentage mosquito-transmission is more calling as severe than sexual-transmission. This can be done by eradicating unnecessary still water bodies, use of bed nets, mosquito repellent and insecticides. Secondly, conduct safe sexual relations especially with one who have been exposed to ZIKV infected regions, bearing in mind that 80% of ZIKV infections are asymptotic [8] . As for women who want or are preparing to get pregnant then if previously had exposed to ZIKV infected regions, having infectious symptoms or not, one is advised to wait until after 8 weeks since last exposure or start of symptoms.
Gaps in This Study
The study has a lot open for further studies. Analytically, the disease free equilibrium has not fully been analyzed, the obtained disease free equilibrium holds for some conditions leaving one side open for investigations. The endemic equilibrium exists but its stability has been discussed numerically, hence calling for further insights in analytically. As for model simulation, assumptions and estimations for current parameters have been used to assign values. Shall it be possible to finely obtain better parameter estimations, model simulation would produce more reliable results. Nevertheless the model can be modified by reducing assumptions so as to make it more realistic. For example, some rates are not constant, therefore may be made non-constant accordingly to fit the reality hence improving the model. Therefore, for some reasons this study calls for more research into the epidemic of ZIKV infections.
Acknowledgements
Sincere thanks to the members of SCIRP for their professional performance, and special thanks to managing editor Karen ZHANG for a rare attitude of high quality. Finally, but not the least it is grateful to the National Natural Science Foundation of China (No. 11371161, 11471133) and the Foundation Research Funds for the Central Universities, Central China Normal University (No. CCNU15A02055) for partially supporting this research financially.
Acronyms
CDC Centers for Disease Control and Prevention in USA
ECDC European Centre for Disease Prevention and Control
MTCT Mother-to-child-transmission
PAHO Pan American Health Organization
![]() Basic Reproduction Number
Basic Reproduction Number
SIR Susceptible Infectives and Recovery
WHO World Health Organization
ZIKV Zika virus
ZVD Zika virus disease
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact health@scirp.org