Random Attractor of the Stochastic Strongly Damped for the Higher-Order Nonlinear Kirchhoff-Type Equation

Guoguang Lin^*, Ling Chen, Wei Wang^*

Department of Mathematics, Yunnan University, Kunming, China.

DOI: 10.4236/ijmnta.2017.62005                

Abstract

In this paper, we consider the stochastic higher-order Kirchhoff-type equation with nonlinear strongly dissipation and white noise. We first deal with random term by using Ornstein-Uhlenbeck process and establish the wellness of the solution, then the existence of global random attractor are proved.

Keywords

Random Dynamical System, Random Attractor, Strongly Dissipation, White Noise

2010 Mathematics Classification: 35K10, 35K25, 35K35

1. Introduction

In this paper, we consider the following stochastic strongly damped higher- order nonlinear Kirchhoff-type equation with white noise:

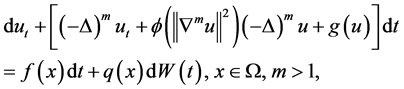(1.1)

with the Dirichlet boundary condition

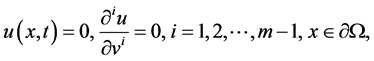(1.2)

and the initial value conditions

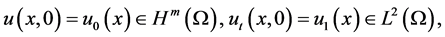(1.3)

where 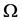is a bounded domain of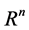, with a smooth boundary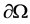, 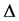is the Laplacian with respect to the variable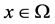, 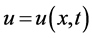is a real function of 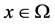and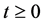, 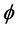is the damping coefficient, f is a given external force, v is the outer norm vector, 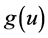is a nonlinear forcing, their respectively satis- fies the following conditions:

1)

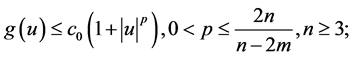
2)

3)

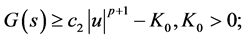
4)

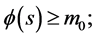
where 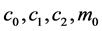are positive constants.

As well as we known, the study of stochastic dynamical is more and more widely the attention of scholars, and the study of random attractor has become an important goal. In a sense, the random attractor is popularized for classic determine dynamical system of the global attractor. Global attractor of Kirchhoff- type equations have been investigated by many authors, see, e.g., [1] [2] [3] [4] , however, the existence random attractor has also been studied by many authors, in [5] , Zhaojuan Wang, Shengfan Zhou and Anhui Gu, they study the asymp- totic dynamics for a stochastic damped wave equation with multiplicative noise defined on unbounded domains, and investigate the existence of a random attractor, they overcome the difficulty of lacking the compactness of Sobolev embedding in unbounded domains by the energy equation. In [6] , Guigui Xu, Libo Wang and Guoguang Lin study the long time behavior of solution to the stochastic strongly damped wave equation with white noise, in this paper, they use the method introduced in [7] , so that they needn’t divide the equation into two parts. In [8] , Zhaojuan Wang, Shengfan Zhou and Anhui Gu study the asymptotic dynamics of the stochastic strongly damped wave equation with homogeneous Neuman boundary condition, and prove the existence of a ran- dom attractor. The other long time behavior of solution of evolution equations, we can see [9] - [19] .

In this work, we deal with random term by using Ornstein-Uhlenbeck process, the key is to handle the nonlinear terms and strongly damped, and is also difficult to be conducted. So far as we know, there were no result on random attractor for the stochastic higher-order Kirchhoff-type equ- ation with nonlinear strongly dissipation and white noise. It is therefore im- portant to investigate the existence of random attractor on (1.1)-(1.3).

This paper is organized as follows: In Section 2, we recall many basic concepts related to a random attractor for genneral random dynamical system. In Section 3, we introduce O-U process and deal with random term. In Section 4, we prove the existence of random attractor of the random dynamical system.

2. Preliminaries

In this section, we collect some basic knowledge about general random dy- namical system ( [9] [10] [11] ).

Let be a separable Hilbert space with Borel s-algebra. Let be the metric dynamical system on the probability space.

Definition 2.1. (see [9] [10] ). A continuous random dynamical system on X over is a -measurable mapping . Such that the following properties hold (1)

1) is the identity on X;

2) for all;

3) is continuous for all.

Definition 2.2. (see [10] )

1) A set-valued mapping, is said to be a random set if the mapping is measurable for any. If is also closed (compact) for each, is called a random closed (com- pact) set. A random set is said to be bounded if there exist and a random variable such that

for all.

2) A random set is called tempered provided for,

for all,

where.

Let Y be the set of all random tempered sets in X.

3) A random set is said to be a random absorbing set if for any tempered random set, and, there exists such that

for all.

4) A random set is said to be a random attracting set if for any tempered random set, and, we have

,

where is the Hausdorff semi-distance given by for any.

5) is said to be asymptotically compact in X if for has a convergent subsequence in X whenever, and with.

6) A random compact set is said to be a random attractor if it is a random attracting set and for and all.

Theorem 2.1. ( [10] ) Let be a continuous random dynamical system with state space X over. If there is a closed random absorbing set of and is asymptotically compact in X, then is a random attractor of, where

Moreover, is the unique random attractor of.

3. O-U Process and Stochastic Dynamical System

Let

, , ,

Let, and define a weighted inner product and norm in E

, ,

,

3.1. O-U Process

O-U process is given by Wiener process on the metric system, we can see ( [11] [12] [13] ).

Let, where, for, meet Itô

equation:. And there is a probability measure P, -in- variant set; so that stochastic process meet the following properties:

1) For, mapping for continuous mapping;

2) Random variable is called tempered;

3) Exist temper set, such that

;

4);

5).

3.2. Stochastic Dynamical System

For convenience, we rewrite the Question (1.1)-(1.3):

(3.2.1)

Let, and (defined in [20] ), then (3.2.1) has the following simple matrix form

(3.2.2)

where

Let, then (3.2.1) can be rewritten as the equivalent system:

(3.2.3)

where

In [14] [15] they have proven that the operator L of (3.2.3) is the infinitesimal generation operator of semigroup in Hilbert space E, is continuous in t and globally Lipschitz continuous in for each. By the classical theory concerning the existence and uniqueness of the solutions [14] [16] [17] , so we have the following theorem.

Theorem 3.2.1. Consider (3.2.3). For each and initial value , there exists a unique function such that satisfies the integral equation

and

For, let the solution mapping of

generates a random dynamical system.

Define two isomorphic mapping:

And inverse isomorphic mapping:

Then the mapping generates a random dynamical system associated with (1.1)-(1.3); and mapping generates a random dynamical system associated with (3.2.2).

Notice that all of the above random dynamical system, are equivalent. Hence we only need to consider the random dynamical system.

4. The Existence of Random Attractor

First, we prove the random dynamical system exists a bounded random absorb set, hence we let be all temper subsets in E.

Lemma 4.1. (Lemma 3.1 of [20] ) Let, for any , we have

(4.1)

where are determined in [20] , , is first eigenvalues of (1.1).

Lemma 4.2. Let is a solve of (3.2.2), then there is a bounded random com- pact set, such that for arbitrarily random set, existence a random variable, so that

(4.2)

Proof. Let is a solve of (3.2.3), applying the inner product of the equation (3.2.3) with, we discover that

(4.3)

where

(4.4)

(4.5)

(4.6)

(4.7)

(4.8)

(4.9)

(4.10)

According to (4.1) and (4.4)-(4.10), we have

(4.11)

where

According to Gronwall inequation, , we have

(4.12)

Because is tempered, and is continuous about t, according to [21] , we can get a temper random variables, such that , we have

(4.13)

Substituting by in (4.12), we know

(4.14)

where

(4.15)

Because is tempered, and is also tempered, hence we let

(4.16)

then is also tempered, is called a random absorb set, and because of

so let

then is a random absorb set of, and.

Next, we will prove the random dynamical system has a compact absorb set

Lemma 4.3. For, let be a solve of (3.2.2), initial value, we decompose, where satisfy

(4.17)

(4.18)

Then

(4.19)

and exist a temper random radius, such that, satisfy

(4.20)

Proof. Let be a solve of (3.2.3), according to (4.17) and (4.18), we know meet separately

(4.21)

(4.22)

Taking inner product (4.21) with, we have

according to Lemma 4.1 and Gronwall inequality, we have

(4.23)

substituting by, and is tempered, then

So, (4.19) is hold. Taking inner product (4.22) with

, we have

(4.24)

according to Lemma 4.1, Lemma 4.2, (4.24) and Young inequality, we have

where are given by Lemma 4.2, and

Due to Gronwall inequality, and substituting by

, we have

According to (4.14) and (4.16), then

Let

Then is tempered, and because

hence, we set

then, for, we have

and is tempered.

Lemma 4.4. (3.2.2) the identified stochastic dynamical system, while exist a compact attracting set.

Proof. Let be a closed ball, radius in space

, because, so is a compact

set in E, for arbitrarily temper random set, for, ac- cording to Lemma 4.3, , so for, we have

+

Theorem 4.1. The random dynamical system has a unique random attractor in E, where

in which is a tempered random compact attracting for.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Yang, Z.-J. (2007) Long-Time Behavior of the Kirchhoff Type Equation with Strong Damping in RN. Journal of Differential Equations, 242, 269-286.
[2]	Yang, Z.J. and Ding, P.Y. (2016) Longtime Dynamics of the Kirchhoff Equation with Strong Damping and Critical Nonlinearity on RN. Journal of Mathematical Analysis and Applications, 434, 1826-1851.
[3]	Chueshov, I. (2012) Longtime Dynamics of Kirchhoff Wave Models with Strong Nonlinear Damping. Journal of Differential Equations, 252, 1229-1262.
[4]	Ono, K. (1997) On Global Existence, Asymptotic Stability and Blowing up of Solutions for Some Degenerate Non-Linear Wave Equations of Kirchhoff Type with a Strong Dissipation. Mathematical Methods in the Applied Sciences, 20, 151-177. https://doi.org/10.1002/(SICI)1099-1476(19970125)20:2<151::AID-MMA851>3.0.CO;2-0
[5]	Wang, Z.J., Zhou, S.F. and Gu, A.H. (2011) Random Attractor for a Stochastic Damped Wave Equation with Multiplicative Noise on Unbounded Domains. Nonlinear Analysis: Real World Applications, 12, 3468-3482.
[6]	Xu, G.G., Wang, L.B. and Lin, G.G. (2013) Global Random Attractor for the Strongly Damped Stochastic Wave Equation with White Noise and Nonlinear Term. Theoretical Mathematics & Applications, 3, 111-122.
[7]	Zhong, C.K., Yang, M.H. and Sun, C.Y. (2006) The Existence of Global Attractors for the Norm-to-Weak Continuous Semigroup. Journal of Differential Equations, 223, 367-399.
[8]	Wang, Z.J., Zhou, S.F. and Gu, A.H. (2012) Random Attractor of the Stochastic Strongly Damped Wave Equation. Communications in Nonlinear Science and Numerical Simulation, 17, 1649-1658.
[9]	Arnold, L. (1998) Random Dynamical Systems. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-662-12878-7
[10]	Chueshov, I. (2002) Monotone Random Systems Theory and Applications. Springer-Verlag, Berlin. https://doi.org/10.1007/b83277
[11]	Guo, B. and Pu, X. (2009) Random Infinite Dimensional Dynamical System. Beijing University of Aeronautics and Astronautics Press, Beijing.
[12]	Lu, D. (1986) Stochastic Process and Its Application. Tsinghua University Press, Beijing.
[13]	Fan, X. (2010) Attractors for a Damped Stochastic Wave Equation of Sine-Gordon Type with Sub-Linear Multiplicative Noise. Stochastic Analysis and Applications, 24, 767-793. https://doi.org/10.1080/07362990600751860
[14]	Pazy, A. (1983) Semi-Groups of Linear Operators and Applications to Partial Differential Equations. Springer Verlag, New York.
[15]	Massatt, P. (1983) Limiting Behaviour for a Strong Damped Nonlinear Wave Equation. Journal of Differential Equations, 48, 334-349.
[16]	Crauelh, N.D. (1988) Random Nonlinear Wave Equations: Smoothness of the Solutions. Probability Theory and Related Fields, 79, 469-508. https://doi.org/10.1007/BF00318783
[17]	Prato, G.D. and Zabczyk, J. (1992) Stochastic Equations in Infinite Dimensions. Cambridge University Press, London, 115-236.
[18]	Lin, G. (2011) Nonlinear Evolution Equation. Yunnan University Press, Kunming.
[19]	Qin, C. and Lin, G. (2010) Random Attractor of the Weakly Damped Stochastic Kirchhoff Equations. Journal of Yunnan University (Nature), 32, 101-108.
[20]	Chen, L., Wang, W. and Lin, G. (2016) Exponential Attractor and Inertial Manifolds for the Higher-Order Nonlinear Kirchhoff-Type Equation. International Journal of Modern Communication Technologies and Research, 4, 6-12.
[21]	Zhao, C. and Zhou, S. (2009) Sufficient Conditions for the Existence of Global Random Attractors for Stochatic Lattice Dunamical Systems and Applications. Journal of Mathematical Analysis and Applications, 354, 78-95.