The Study on the Relationship between Agricultural Product Price Fluctuation and Inflation ()
1. Introduction
At present, the domestic scholars on the relationship between agricultural prices, inflation expectations and inflation are mostly concentrated in agricultural product price fluctuations and inflation causal analysis, the majority of the study that agricultural price fluctuations are contributing to inflation. The research is helpful for us to deepen the understanding of the relation between agricultural product price and inflation, but these researches still have the following shortcomings: Firstly, we do not take into account the effect of agricultural price change on inflation expectation, the expected impact of agricultural price fluctuations is the most direct, and this expectation has on the macroeconomic operation and the government’s macro-control has had a great impact, most scholars in the research process is ignored this important part ; Secondly, there is no agricultural price fluctuations, inflation expectations and inflation into a dynamic system for analysis, in-depth study of the interaction between the three [1] [2] [3] [4] [5] . Based on this, this paper builds up the VAR model on the basis of introducing the important factor of inflation expectation, investigates the mutual relations among the three aspects from the long-term and the short- term, and provides the decision-making for the government to stabilize the price level and maintain the steady growth of the economy reference.
2. Model, Variable Selection and Data Source
The empirical research in this paper mainly analyzes the relationship between agricultural commodity price fluctuation, inflation expectation and inflation from the following two aspects. First, the long-run equilibrium angle using the method of co-integration analysis studies the interaction between them. The second is the short-term dynamic relationship, mainly using impulse response function and variance decomposition method for impact response and contribution analysis.
Vector Auto Regressive (VAR) is a model based on the statistical properties of data. The idea is to construct each model as a function of the hysteretic of all endogenous variables in the system. The model is often used in predicting interconnected time series systems. It is also commonly used to analyze the dynamic impact of stochastic disturbances on variable systems and to explain the impact of various economic shocks on the formation of economic variables [6] . The mathematical expression of the VAR (p) model is:

Where 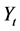 is the
is the 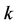 endogenous variable vector,
endogenous variable vector, 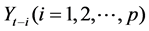 is the lagged endogenous variable vector,
is the lagged endogenous variable vector, 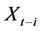 is the
is the 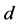 dimensionally exogenous variable vector,
dimensionally exogenous variable vector,  ,
, 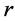 are the lagged order of the endogenous variable and the lagged order of exogenous variables..
are the lagged order of the endogenous variable and the lagged order of exogenous variables..  is the
is the 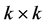 dimensional coefficient matrix and
dimensional coefficient matrix and 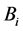 is the
is the 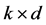 dimensional matrix. These matrices are the parameter matrix to be estimated.
dimensional matrix. These matrices are the parameter matrix to be estimated. 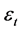 is a vector of
is a vector of 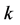 dimensional random error terms, which has no correlation with the values of the hysteretic and the variables to the right of the equation, but they can be correlated with each other at the same time.
dimensional random error terms, which has no correlation with the values of the hysteretic and the variables to the right of the equation, but they can be correlated with each other at the same time.
In this paper, the monthly price index data from January 2011 to November 2015 was used to analyze the long-term and short-term relationship between agricultural commodity price fluctuation, inflation expectation and inflation. The relevant variable description and source are as follows:
1) Price index of agricultural products (AP). This paper selects the retail price index of food retail price index as the proxy variable of the agricultural price index. The retail price index of food is a relative number that reflects the trend and fluctuation of the retail price of food market in a certain period. It directly affects the residents’ feelings about the price fluctuation, which affects their expectation.
2) The level of inflation expectations (IE). In this paper, consumer expectations index is chosen as the proxy variable of inflation expectation. It is the expectation of consumer’s change in future economic life. It is the general consumer’s income, savings, macro economy, consumption expenditure, employment situation, purchasing durable consumer goods and quality of life in the next year is expected and the next two years in the purchase of housing and renovation, the purchase of cars and the next six months the stock market is expected to change [7] .
3) Inflation Index (IR). Using the Consumer Price Index (CPI) selected by most of the studies to represent the level of inflation.
The above data are derived from the National Bureau of Statistics website and the CCER China Economic and Financial Database, in order to eliminate seasonal patterns, so that changes in the sequence of time points to better reflect the underlying laws of the data, so that the statistics of different seasons. The data are comparable, this paper uses the X-11 method for seasonal adjustment [8] . In addition, since the natural logarithm transformation of the data does not affect the original co-integration relationship between the data and can linearize the trend, it can eliminate the heteroscedasticity phenomenon in the time series to a certain extent. A logarithmic transformation was performed.
3. Empirical Analysis
3.1. Data Smoothness Test
When using co-integration test to carry out empirical analysis, it is required that all the time series of co-integration test must meet the conditions of horizontal instability and same order differential stationary. Therefore, we must first test the stability of the variables. In this paper, the ADF (Augmented Dickey-Fuller test) unit root test method to test the stability of the various time series variables, test results in Table 1.
From Table 1, we can see that the original time series have unit roots, which are no stationary sequences. After all the first-order differences, they are all stable, so they are first-order single-sequence I (1).
3.2. Long-Term Relationship between the Empirical Analyses
Since each variable sequence is a first-order differential stationary series, the Johansen-Juselius co-integration test can be used to determine whether there is a long-term co-integration relationship among the three variables.
(1) Determination of the lag order p
An important issue in the VAR model is the determination of the lag order. In
![]()
Table 1. The stationary test of variables.
Note: The test form brackets represent the constant term, the trend term and the lag order, lag order determined by the SIC and AIC criteria, Δ said first-order difference operator.
this paper, the Lagrange Criterion is used to evaluate the most reasonable VAR model to establish the lag time. It can be seen from Table 2 that the minimum lag time is given in each of the six evaluation criteria. According to the criteria of LR, FPE and AIC, the optimal lag time is 1 and the VAR (1) model is reasonable.
(2) Granger test (Granger Causality Tests)
In order to study the interaction between DLnAP, DLnIE and DLnIR, Granger causality test is carried out in this paper. The test results are shown in Table 3.
It can be seen from Table 3 that the agricultural price fluctuation is the Granger cause of the change of the residents’ inflation expectation, but the change of the inflation expectation is not Granger cause of the agricultural price fluctuation, that is, there is one-way Granger causality; There is no Granger causality relationship between agricultural price fluctuation and inflation fluctuation, which is different from other scholars’ research. There is a two-way Granger causality relationship between inflation expectation change and inflation level change.
(3) Co-integration test
In order to test the existence of long-term stable equilibrium relationship between price fluctuation of agricultural products, inflation expectation and inflation level, the Johansen co-integration test based on regression coefficient is used to test the above variables. The results are shown in Table 4.
The results in Table 4 show that there is no common long-term stochastic trend between LnAP, LnIE and LnIR. That is, there is no cointegration relationship between agricultural product price fluctuation, inflation expectations and inflation. This may be due to the paper selection of the time period and variables are different from other scholars.
![]()
Table 2. Judgment result of VAR optimal lag.
Note: * indicates the minimum lag time given by the criterion.
![]()
Table 3. The granger causality test results.
Note: After the original logarithm sequence after the differential DLnAP = LnAPt − LnApt−1, this represents the price of agricultural products fluctuations.
![]()
Table 4. The Cointegration test results.
Note: The above test contains a constant but not a trend.
3.3. Analysis of Short-Term Dynamic Relationship
In order to further analyze the interaction of the three variables in short-term changes on each other, the following will use impulse response function and variance decomposition for analysis. Since there is no co-integration relationship among the three variables, this paper is based on the VAR (1) model, which is based on the first order difference of the logarithm sequence of three variables.
(1) Impulse response function analysis
Impulse response function (IRF) characterizes the effect of the change or impact of each endogenous variable on its own and all other endogenous variables and reflects the dynamic characteristics of the system. The specific shock response diagram is shown in Figure 1, Figure 2 and Figure 3.
Figure 1 shows the response of agricultural prices to inflationary expectations, inflation and a standard deviation of itself. It can be seen that a positive impact of unit standard deviation on both inflation expectations and inflation will have a positive impact on agricultural prices, and the response function of the agricultural product price is the largest in the first period, reaching 0.02, then decreasing rapidly and decreasing from the standard deviation of the positive unit. The second phase began to slow down; in addition to agricultural prices for the positive impact of the three are beginning to weaken in the seventh to close to zero.
Figure 2 shows the response of inflation expectations to a standard deviation shock from agricultural commodity prices, inflation, and itself, where the response to one standard deviation shock for inflation is at a maximum of 0.01 in the current period, followed by a rapid decrease Weak, between the second and third phases only a small change from the third period began to slow down; For a standard deviation of prices of agricultural products and impact from inflation, inflation expectations of the performance is basically the same reaction, are rising rapidly from the beginning of the current period, the second phase of maximum 0.03 and 0.04, then began to slowly weaken. The difference is that for a positive impact from a standard deviation of the price of agricultural products, the reaction of inflation is expected to be negative in the current period and then quickly to a positive response.
Figure 3 shows the response of inflation to a standard deviation from agricultural commodity prices, inflation expectations and its own standard deviation, which imposes a standard deviation on the price of agricultural products. The inflation response function shows a maximum of
0.065 in
the first period, to the second period of 0.01, and then began to slow down; for inflation from
![]()
Figure 1. Response of DLNAP to Cholesky One S.D. Innovations.
![]()
Figure 2. Response of DLNE to Cholesky One S.D. Innovations.
![]()
Figure 3. Response of DLNR to Cholesky One S.D. Innovations.
the expected standard deviation of a shock, the reaction of inflation is positive, in the first 2 to reach the maximum, and then began to slow down; and from their own impact, the reaction of inflation in the current maximum of 0.025, began to weaken, also in the first 7 to close to 0.
It can be seen that the response of the impulse response is consistent with the theoretical expectation. The response of agricultural price fluctuation to the impact from inflation expectation and inflation is positive, but the effect is relatively weak, and the reaction of inflation expectation to a shock from agricultural price is also positive, indicating that when the price of agricultural products up, the residents in the short term inflation expectations will follow the uplink, but the impact lasted only about three or so disappeared.
(2) Variance decomposition analysis
The variance decomposition describes the relative importance of the impact of each variable in the VAR model on the dynamic changes of the system variables. The main idea is to decompose the system’s prediction mean square error into its contribution rate of other shocks, so as to understand the relative importance of each variable impact on model endogenous variables. We then proceed to variance decomposition of the variables in the VAR model to further examine the factors that affect the price volatility of agricultural products, inflation expectations and inflation. Figure 4 to Figure 6, respectively, report the variance of agricultural price inflation, inflation expectations and inflation decomposition results.
From Figure 4 we can see that inflation expectations and inflation on the contribution of agricultural price fluctuations are relatively low, in the sixth phase was only 2.79% and 3.46%, then has been relatively stable, agricultural price fluctuations on their own contribution rate accounted for 93% to 100%,
![]()
Figure 4. Variance decomposition of DLNAP.
![]()
Figure 5. Variance decomposition of DLNE.
![]()
Figure 6. Variance decomposition of DLNR.
indicating that agricultural price fluctuations are mainly from their own impact.
Figure 5 shows that the contribution rate of inflation to inflation expectations in the second period reached 10.3%, then remained at 11.6%, and relatively stable; agricultural price fluctuations on the contribution rate of inflation expectations in the second period reached 5.67%. Inflation expectations of its own volatility in the first accounting for up to 99%, and then rapidly decline from the second phase and gradually stabilized at 82%.
It can be seen from Figure 6 that 77% to 87% of the fluctuation in inflation can be explained by the fluctuation of agricultural product price. Only 0.8% to 6.5% is explained by the fluctuation of inflation expectation. The rest is explained by itself. Among them, in the first period, the impact of agricultural price fluctuations on inflation the most, explained 87% of the volatility, and then declined rapidly from the second period began to gradually stabilize, and inflation expectations volatility has been maintained at a lower interpretation level.
The variance decomposition shows that inflation expectation and inflation contribute less to the fluctuation of agricultural product price, while the contribution rate of agricultural product price fluctuation to inflation fluctuation is the largest, and the fluctuation of inflation expectation is explained by its own fluctuation.
4. Conclusions and Suggestions
This paper makes an empirical study on the relationship between the price fluctuation of agricultural products, inflation expectations and inflation in China between January 2011 and November 2015. The main conclusions are as follows:
(1) There is no long-term stable equilibrium relationship between agricultural product price fluctuation, inflation expectation and inflation, but there exists Granger causality between them, among which there is one-way causal relationship between agricultural product price fluctuation and inflation expectation. That is, the fluctuation of agricultural product price fluctuation can Granger cause inflation expectation change, but the change of inflation expectation can not be significant. Granger causes the fluctuation of agricultural product price, which is consistent with our expectation. It proves that the rise of agricultural price can cause inflation expectation; there is a two-way Granger causality between the expected change and the change of inflation, and there is no Granger causality between agricultural price fluctuation and inflation fluctuation. This conclusion also agrees with the research results of some scholars, which shows that the price increase of agricultural products only one form of inflation, rather than the cause of inflation, the impact of rising agricultural prices on inflation is passed through the impact of inflation expectations, because the residents of the demand for agricultural products is rigid, and its price increases will have a direct impact the residents of the inflation expectations. Although inflation expectations are not equal to the actual inflation, but inflation expectations will continue to accumulate, resulting in spiraling increases in commodity prices and inflation expectations, and ultimately evolved into significant inflation.
(2) Using the impulse response function and the variance decomposition to analyze the fluctuation conduction intensity and efficiency between the three, the results show that the inflation expectation and the fluctuation of inflation have a lag in the transmission of the agricultural price fluctuation, and their transmission effect with time to strengthen, but the effect is not obvious. The impact of agricultural price fluctuations and inflation shocks on inflationary expectations in the second period reached the maximum effect, while the impact of inflation on agricultural products from the impact of price fluctuations in the current period to reach the maximum effect, and this effect is positive. But since the first period after the rapid decline, in addition, inflation from the impact of inflation expectations in the current period there is a positive response, lagging behind a maximum.
In summary, although the long term, agricultural prices, inflation expectations and inflation does not exist between the stable equilibrium relationship, but the agricultural price fluctuations are inflation expectations of Granger reasons, and inflation expectations and inflation. There is also a two-way Granger causality, and the transfer between the three short-term fluctuations in the transfer effect is still more obvious, especially agricultural price fluctuations on the role of inflation in the short term more significant. In addition, although the impact of agricultural price fluctuations on inflation expectations is not very significant, but to some extent, or exacerbated the formation of inflation expectations.
Combined with the actual situation of China’s current stage and the conclusions of empirical analysis, this paper presents the following recommendations:
(1) The impact of agricultural price fluctuations on inflation in the short term is obvious. Therefore, it is necessary for the government to strengthen the regulation of the market, maintain the stability of agricultural prices and avoid a sharp increase in inflation, on the one hand by guiding the market to stimulate the enthusiasm of farmers to ensure the supply of agricultural products and enhance supply confidence, on the other hand to control the current agricultural products to be hype the market risk, to avoid causing a wider range of acts of price hikes; see, control of China’s inflation, it should not start from the inhibition of agricultural prices.
(2) The rise of agricultural prices on the formation of inflation expectations will have a positive impact, and inflation expectations will continue to accumulate and promote inflation, it is imperative to strengthen the management of inflation expectations, not only from the stability of agricultural prices to manage inflation expected, but also should strengthen the scientific guidance of public opinion, and guide people to rationally deal with price increases, to avoid blindly follow the wrong message, exacerbate the formation of inflation expectations.