1. Introduction
Although 3 centuries have elapsed since Newton set forth his gravitational law, physiology has been unable so far to create an exact theoretical value for the universal gravitational constant with no available values of the gravitational constant values except those values concluded by scientific experiments, especially conducted for obtaining the most accurate values of this constant.
We are going, in this research, to surmount this problem by way of setting forth a universal gravitational constant sole theory value, to be calculated through an index of a law known in the Khromatic theory as “The Law of Gravitational Constant” [1] , although another problem yet lies here, which is that all results of experiments relating to determining the value of gravitational constants are confined to two values: a greater value and a lower value.
To overcome this problem, we put forth a supposition that a certain marginal velocity can be a basis for calculating a gravitational greater value acceptable as an ideal value within a certain error rate. And to ascertain the validity of the hypothesis we compared, through discussion, the values we obtained with those on the gravitation Table 2 of 2014 CODATA, as the comparison showed that in both cases the values were significantly close together, a thing that enabled us to solve the discrepancy between the theoretical and experimental values, consequently modifying Table 2, thereby we will have left behind an era of incessant attempts to find out the most accurate value of the gravitational constant.
2. Finding the Accurate and Approximate Value of the Gravitation Constant
2.1. The Precise Ideal Value of G
The law of gravitational constant looks like this:
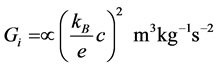
as,
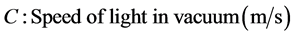
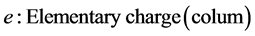
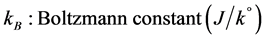
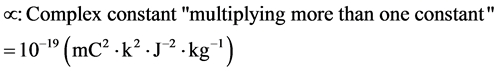
We are not going in our discussion, to deal with the method of the inference of this law, because of that it will be through another search that will be published completely, but we will content ourselves by reviewing the law and finds the precise ideal value of gravity through it.
Taking the values of the constants above from an abbreviated list of the 2014 CODATA recommended values of the fundamental constants of physics and chemistry, we get
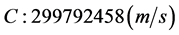
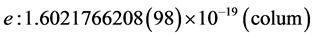
So, using substitution in the value of constants we get the precise value of the gravitation constant equaling:
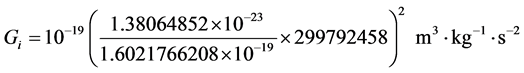
2.2. The Expected Value of the Gravitation Constant
Perhaps the ideal precise value of the gravitation constant is suitable for the static large blocks or those having negligible velocity-induced increment.
As for small masses moving at high speeds, it is more suitable to deal with relativity when calculated, however, we can handle expected values of the gravitational constant for experiments in which the body's velocity is so limited that the block's increment may be overlooked.
And to find such values, we can suppose that the block’s laboratory speed limit should not exceed the orbital speed of electron in an atom of hydrogen and consequently the maximum expected gravitational value should not exceed a maximum value of the gravitational constant that is calculable using the equation.
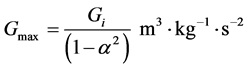as,
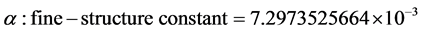
And on calculation of this value we get the following:
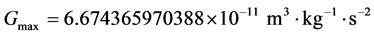
Hence we can deduce the ideal standard uncertainty vale 
from the equation:
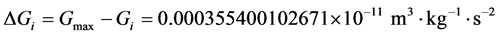
And the ideal value of the relative standard uncertainty is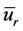 
of the equation:
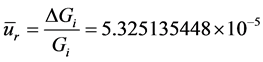
which is a somewhat an acceptable value.
3. Relationship between ![]()
and ![]()
Since
![]()
![]()
,
Thus
![]()
,
and
![]()
4. Discussion
In this discussion we are going to compare the ideal values we had got by theoretical means and the documented experimental values in CODATA gravitational tables, and we will show that the values are close in both cases.
4.1. Comparison of the Ideal and Results of Measurements of Gravitational Constant
Table 1, borrowed from CODATA Recommended Values of the Fundamental Physical Constants, 2010, summarizes the results of measurements of the Newtonian parameter of gravitation relevant to the 2010 adjustment [2] .
In this table there are three groups of measurements [3] .
・ The first such group consists of six measurements with the average value of
![]()
Standard uncertainty ![]()
and relative standard uncertainty 28.5 ppm;
・ The second one consists of four measurements with the average value of
![]()
Standard uncertainty ![]()
and relative standard uncertainty 24 ppm;
・ The third one consists of one measurement with the value of
![]()
Standard uncertainty ![]()
and relative standard uncertainty 40 ppm.
Therefore, we conclude that the ideal value of the gravitational constant equals the sum
![]()
Table 1. Summary of the results of measurements of the Newtonian constant of gravitation relevant to the 2010 adjustment.
![]()
which is extremely close to the average value G1, that equals the following sum
![]()
So we can choice the first group of G measurements as the best precision group of all others.
4.2. Comparison of the Ideal and 2014 CODATA-Recommended Value of the Gravitational Constant [4]
We learn from Table 2 the recommended values of 2014 CODATA [4] as follows:
That is, based upon the above table, the experimental value of the gravitational constant should range from a maximum value of ![]()
equaling ![]()
to a maximum value ![]()
equaling ![]()
with ![]()
as the arithmetic mean of the two values that equals![]()
.
4.2.1. The Ideal Value of the Gravitational Constant Equals the Sum
![]()
which is extremely close to the gravitational experimental value, that equals the following sum
![]()
4.2.2. Comparison of the Extent and Rate of Error
When comparing the ideal quantity of standard uncertainty, which equals
![]()
To its counterpart mentioned in Table 2, which has the value:
![]()
we find great similarity in values.
4.2.3. Comparison of the Relative Error Rate
Likewise, when comparing the ideal value of the relative standard uncertainty, which equals:
![]()
To its counterpart contained in Table 2 which has the value:
![]()
![]()
Table 2. 2014 CODATA- recommended values of gravitation G, ∆G, ![]()
, Concise form.
![]()
Table 3. Updated the values of gravitation G, ∆G, ![]()
, Concise form.
we also find great similarity in values.
Therefore, we conclude that all ideal values we have obtained through the theoretical equations are extremely close to their experimental counterparts which we had got from Table 2, which shows the recommended values of 2014 CODATA, except that the ideal values are more accurate, having been theoretically concluded, and as such, the data of Table 2 may be updated and substituted for the ideal values as illustrated below in Table 3.
5. Conclusions
There is a precise ideal value of the universal gravitational constant which equals 6.674010551359 × 10−11.
That may be calculated through a theoretically concluded equation of its own, and the cause of discrepancy of the gravitation value is attributable to the circumstances of the experiment as well as the sophistication of the nature and speed of particles used to measure the gravitational constant in such experiments.