1. Introduction
Among the problems of global health, cancer has become one of the main subjects of research for different fields of knowledge. Many of these researches are conducted with the goal of developing and evaluating new forms of therapy or just new methodologies or treatment protocols. As there is a wide variety of algorithms for tomographic reconstruction and absorbed dose calculation in radiation therapy applications involving various mathematical techniques have been proposed and are still constantly improved [1] .
From a mathematical point of view, the challenge is to deliver a high radiation dose to the tumor, enough to eliminate them, and simultaneously minimize radiation in the surrounding regions, composed of healthy tissue, while minimizing the complications in these regions.
Among these techniques, linear programming stands out for its intense and wide application and the results obtained are considered promising. The objective of treatment is to eliminate tumor cells by radiation, and at the same time it seeks to prevent the destruction of surrounding healthy cells also affected by radiation. For planning the treatment with radiosurgery computerized tomography images are scanned and merged with magnetic resonance images obtained previously. From these images critical structures and tumor are located and then many computations may be performed to determine three-dimensional isocenters, isodose curves, dose to be prescribed, position, number and its weight conformal isocentric fields, among others. Such plan is prepared by the surgical team in order to obtain an adequate and optimal treatment for each case.
The treatment plans are commonly based on the desired dose levels for specific types of tumors and organs at risk in the irradiated region. These levels’ dose is chosen so that high probability of cure is achieved, while the likelihood of complications in any organ is minimal risk. The aim of this paper is to show the optimal planning in radiotherapy looking for an optimal solution using the Simplex Method and its comparison with Interior Points Methods.
2. Linear Programming in Radiotherapy
In recent decades, the impact of cancer in society got large attention, becoming a global concern, and in Brazil one of the top positions in the macro-regions mortality rates, along with the diseases of the circulatory system, external causes, among others. Cancer is a disease that begins when a genetic mutation in the DNA of the cell, where the control mechanism of normal tissue growth is changed. The methods for cancer treatment are: surgery, radiotherapy and chemotherapy.
The radiotherapy treatment aims elimination of cancerous cells through radiation or relief of symptoms and at the same time seeking to avoid destruction of surrounding healthy cells also affected by radiation. From a mathematical point of view, the challenge is to deliver a high dosage radiation into the tumor, sufficient for eliminating and stopping the growth of tumor cells, whilst minimizing the radiation neighboring regions composed of healthy tissue, while minimizing complications in those regions which are often critical.
At the beginning of the use of radiotherapy, was applied high doses of radiation, as well as the patient be able to afford. The dose constraint was generally established the tolerance of the skin [2] . There are two main types of radiation: brachytherapy and teletherapy. Give yourself will focus in this work to the second type. In this case, neither the radiation source nor device that emits, are in direct contact with the patient. Therefore, the radiation reaches beyond the tumor all organs and tissues that are in the way. In the brachytherapy radiation source is placed inside the patient in the region that would receive treatment. It is a kind of non-permanent radioactive implant [3] . Usually for the treatment using a beam with rectangular form, which passes through different types of patient body tissues, and depending on the attenuation and the depth of tissue, a large amount of energy is deposited at various points within the body. For radiotherapy treatment should take into account the depth dose distribution in the central axis and characterizing the radiation beam. To represent and to have the concept of the dose distribution and absorption throughout the volume and makes up the isodose curve, which are lines representing points of the same dose in a given arrangement of radiation beams. For the mathematical calculation, they are used clinical tumor data for each patient treated. These calculations can be performed by mathematical models through linear programming.
Mathematical Formulation
When cancer is diagnosed and there are medical indications for treatment by radiotherapy, various tests are performed on the patient, in order to learn about the location, form and tumor volume, as well as critical tissues in the region to be treated. The use of computerized tomography exams for reliable data collection and in the radiosurgery is required along with a computed tomography an magnetic resonance exam.
Based on these data, the dose to be received in the tumor and the volume to be irradiated may be prescribed by the doctor radiotherapist. Together with a physical, the radiation oncologist can then by the analysis of isodose curves can define the best type of treatment and the technique to be used. After obtaining the images by computed tomography or magnetic resonance imaging, the minimum dose to be applied to the tumor is prescribed as the maximum doses that critics and healthy tissue can receive. Through these images, it makes the selection of the anatomical structures of interest.
On the images obtained, the structures of interest can then be mapped (and critical lesion tissue) through a pixelation. Each pixel is related to an electron density and receives specific coordinates (i,j), which will be used in the creation of conformational planning or 3D treatment planning, as shown in Figure 1.
To illustrate, suppose a dimensional image m × n where each element’s image is called pixel representing a part of the human body. Also, consider que each angle is composed of sub-rays. Modern processing systems are capable of performing complex combinations between these sub-beams. The number of angles is fixed such that are considered k angles locations to issue the main beam Radiation. Each one containing 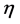 sub-beams. Modern processing systems are able to perform combinations among these sub-beams to use them over a full arc, making planning using
sub-beams. Modern processing systems are able to perform combinations among these sub-beams to use them over a full arc, making planning using 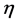 sub-beams. This decomposition of the radiation beams is based on the theoretical and practical foundations of radiotherapy with modulated intensity. The geometry of a model using elementary beams, where
sub-beams. This decomposition of the radiation beams is based on the theoretical and practical foundations of radiotherapy with modulated intensity. The geometry of a model using elementary beams, where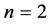 ,
, 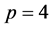 and
and 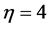 is shown in Figure 2. The inter-
is shown in Figure 2. The inter-
vals between the angles  and the initial angle is (usually) zero.
and the initial angle is (usually) zero.
In the treatment planning, once defined the coordinates (i,j) of pixels, with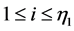 ,
, 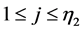 , one computes the total dose
, one computes the total dose 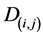 being received by the patient in each pixel coordinates (i,j). Thus, one can estimate the dose to be received in each patient’s tissue (critical, healthy and tumor), the area to be treated worrying not to exceed the dose supported by healthy and critical tissues and a dose sufficient enough to eliminate the tumor.
being received by the patient in each pixel coordinates (i,j). Thus, one can estimate the dose to be received in each patient’s tissue (critical, healthy and tumor), the area to be treated worrying not to exceed the dose supported by healthy and critical tissues and a dose sufficient enough to eliminate the tumor.
This model can be represented by the following:
 (1.0)
(1.0)
where,
・  represents the total dose received by the patient in position (i,j);
represents the total dose received by the patient in position (i,j);
・  represents the nominal dosage issued by the radius p in position (i,j);
represents the nominal dosage issued by the radius p in position (i,j);
・ w represents the weight of the dosage emitted by beams;
・ l represents the minimum dose to be received by the tumor;
・ 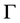 represents the subset of positions where the tumor is located;
represents the subset of positions where the tumor is located;
・ n represents the number of rays;
・ m represents the total number of pixels.
It is possible to formulate a model with weights in each region of the patient privileged or penalize some areas the dosing quantity to be received. Given the delineation of structures, the treatment plan should be developed in order to manage the radiation dose on the tumor, thus seeking the homogeneity of the treatment plan, according to the determination of the dose prescription of regions of interest.
Defining the following subsets:
・ R represents the subset of positions where critical tissue (healthy) or critical framework;
・ N represents the subset of positions where the other healthy tissues.
It is possible to formulate a model with weights in each region of the patient privileging or penalizing some areas where the dosing quantity is received.
Given the delineation of structures, the treatment plan should be developed in order to manage the radiation dose to the tumor, thus seeking the homogeneity of the treatment plan, according to the determination of the dose prescription of regions of interest.
Holder [4] formulates some models of Linear Programming by weightings in each region of the patient’s image, considering or privileging the type of tissue to be exposed to radiation doses.
As 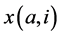 the dose over the i-th subfeixe, to
the dose over the i-th subfeixe, to 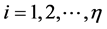 a-th angle to
a-th angle to 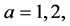
![]() and
and ![]() the distance between the source positioned at an angle to sending subfeixe i (de dose
the distance between the source positioned at an angle to sending subfeixe i (de dose![]() ) and pixel p. The dose deposition in the pixel p due i-th subfeixe of the a-th angle
) and pixel p. The dose deposition in the pixel p due i-th subfeixe of the a-th angle ![]() is defined as:
is defined as:
![]() (1.1)
(1.1)
The term S represents the geometric area of pixel p which receives the dose![]() . With the component
. With the component ![]() may be constructed the dose deposition of matrix A, where the rows in A are indexed by p and the columns are indexed by
may be constructed the dose deposition of matrix A, where the rows in A are indexed by p and the columns are indexed by![]() , as shown in the matrix (1.2), thus the matrix A has dimension
, as shown in the matrix (1.2), thus the matrix A has dimension![]() .
.
![]() (1.2)
(1.2)
Most research has used optimization models with linear constraints, with one of the two most obvious objective functions, maximizing the dose to the tumor and minimize the dose to the critical structure. Since this often leads maximization at high doses, other studies seek to maximize the minimum dose of the tumor or reduce the maximum dose of critical structure [5] .
The goals listed below indicate that this problem has many parameters to consider in deciding what would be desirable for a treatment plan:
・ Transmitting a uniformly lethal dose in the tumor region;
・ Transmitting radiation as small as possible in critical structure;
・ Obtain a total dose as small as possible;
・ Reducing the frequency of high doses outside the region of the tumor;
・ Controlling the number of rays used in the treatment plan.
In search of uniform doses, Holder proposed a linear optimization model to assist in the optimal planning of radio surgery. This model has been widely cited in the literature by presenting good results in terms of conformal plans. So we opted for the study and implementation of this model, which will be discussed below.
Consider, ![]() tumor pixel number,
tumor pixel number, ![]() the number of pixels of the critical structure and
the number of pixels of the critical structure and ![]() the number of pixels of healthy tissue. Therefore the total number of pixels is given by
the number of pixels of healthy tissue. Therefore the total number of pixels is given by![]() . Thus, in the model of Holder, the dose deposition matrix is divided into three parts:
. Thus, in the model of Holder, the dose deposition matrix is divided into three parts:
![]() (1.3)
(1.3)
The rows of the dose deposition matrix are rearranged so that T is related to the set of pixels comprising the lesion or tumor, C to pixel set included the critical tissue or organs at risk and G to the pixel set of remaining healthy tissue.
Thus, the sectional image of computed tomography is converted into an array of pixels, which are classified to represent tumor and non-tumor regions. Due the division into pixels, the model that will be presented, the prescription dose is given in the form of vector and defined by four boundaries, with the following notation:
・ ![]() represents the upper limit vector to radiation in the tumor (
represents the upper limit vector to radiation in the tumor (![]() );
);
・ ![]() represents the lower limit vector to the tumor radiation (
represents the lower limit vector to the tumor radiation (![]() );
);
・ ![]() represents the upper limit vector for radiation in the critical structure (
represents the upper limit vector for radiation in the critical structure (![]() );
);
・ ![]() represents the upper limit vector to radiation in the remaining healthy tissue (
represents the upper limit vector to radiation in the remaining healthy tissue (![]() ).
).
Obviously ![]() and
and ![]() hold. If an uniform lethal dose is transmit ted to the tumor, the upper and lower limit to the tumor pixels are obtained through the established goals.
hold. If an uniform lethal dose is transmit ted to the tumor, the upper and lower limit to the tumor pixels are obtained through the established goals.
Assuming that the targets set for a cell are![]() , the values
, the values ![]() and
and ![]() they are generally (1 + e)
they are generally (1 + e) ![]() and (1 − e)
and (1 − e)![]() , respectively, where
, respectively, where ![]() is the percentage of variation for tumor strength and uniformity is termed the tumor level. Typical values
is the percentage of variation for tumor strength and uniformity is termed the tumor level. Typical values ![]() are found in the literature varying from 0.02 to 0.15.
are found in the literature varying from 0.02 to 0.15.
The vector ![]() represents the largest amount of radiation allowed for any pixel (healthy). Generally healthy tissues should not receive more than 10% of the dose established for the tumor. That is,
represents the largest amount of radiation allowed for any pixel (healthy). Generally healthy tissues should not receive more than 10% of the dose established for the tumor. That is,![]() . The rows of dose deposition array are rearranged in row a representing cancer regions critical structures and the remaining healthy tissue. This reordering is represented by the
. The rows of dose deposition array are rearranged in row a representing cancer regions critical structures and the remaining healthy tissue. This reordering is represented by the![]() ,
, ![]() and
and ![]() as shown in (1.3).
as shown in (1.3).
The sub-beams that do not reach the tumor are removed by the elimination of the columns that have the zero vector in the corresponding column of submatrix![]() . Thus, without loss of generality let us assume that the
. Thus, without loss of generality let us assume that the ![]() matrix does not have null columns. Therefore,
matrix does not have null columns. Therefore, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
3. Linear Optimization Problem
The model proposed by [4] allows a number of constraints on the amount of limitation of the dose in each tissue type. The objective function is represented by the weighted sum of three goals:
・ ![]() , which measures how close the minimum dose the found plan apply in the tumor region;
, which measures how close the minimum dose the found plan apply in the tumor region;
・ ![]() , which measuring the amount of radiation received by the prescribed critical region;
, which measuring the amount of radiation received by the prescribed critical region;
・ ![]() , which measuring the amount of radiation prescribed gin other healthy tissues.
, which measuring the amount of radiation prescribed gin other healthy tissues.
The positive scalar w weight the importance of formulating a plan to get the minimum dose in the tumor region, i.e., large values of w make ![]() to be as small as possible. It would be desirable if there were a finite value for
to be as small as possible. It would be desirable if there were a finite value for ![]() such that the optimal value of the component
such that the optimal value of the component ![]() were zero which would ensure the tumor receives as much radiation level as possible.
were zero which would ensure the tumor receives as much radiation level as possible.
The proposed model can be represented as follows:
![]() (1.4)
(1.4)
where,
・ w: positive scalar;
・ x: dose of sub-beams entering the image to reach the pixel p, (![]() );
);
・ ![]() ;
;
・ ![]() ;
;
・ ![]() .
.
The constraints![]() , and
, and![]() , are called elastic constraints, since their limits may vary according to the vectors t, c and g, respectively.
, are called elastic constraints, since their limits may vary according to the vectors t, c and g, respectively.
The matrices ![]() and
and ![]() define how to measure elasticity, and
define how to measure elasticity, and ![]() and
and ![]() control the penalty or reward relative to elasticity.
control the penalty or reward relative to elasticity.
Fixed values ![]() and
and ![]() define a set of elastic functions. And these are incorporated for the following reasons:
define a set of elastic functions. And these are incorporated for the following reasons:
1) The elastic constraint ensures that a set of elastic functions is always strictly feasible;
2) The difference of the limits on the elastic functions allow us to incorporate different treatment goals.
As previously discussed, the model (1.4) is a linear programming problem and can be solved by the simplex method. To solve this problem, means determining ![]() and
and ![]() that optimize the objective function and achieve the goals set the best way possible.
that optimize the objective function and achieve the goals set the best way possible.
Thus, with the optimal dose of vector x is possible to compute the total dose of radiation, or total for each pixel. Given the optimal dose distribution in tissues it is possible to construct isodose curves.
4. Simplex Method Applied to the Treatment Model for Radiotherapy
As the image is in pixels, the dose limits should be divided by the number of pixels of the respective bodies, to ensure the uniformity of the dose [6] . Therefore, the objective
function, the values dose limits will be ![]() and
and![]() , where
, where
![]() ,
, ![]() ,
, ![]() and e is unit vector.
and e is unit vector.
Supposing, ![]() , and replacing bounded constraint
, and replacing bounded constraint![]() , as L = I, Uc = I and
, as L = I, Uc = I and![]() , we obtain following problem:
, we obtain following problem:
![]() (1.5)
(1.5)
Thus, we obtain the following constraint matrix:
![]() (1.6)
(1.6)
5. Computational Results
This section will present and discuss some results obtained in the computational implementation of the mathematical model (1.4), aiming to help in optimal radiotherapy planning. The problem was solved in a Microcomputer-macbook pro, 2.5 GHz processor, i5, 4 GB memory, 1600 MHz, DDR3.
Following the described methodology, initially the cancer is diagnosed and indicated with radiation therapy. Thereafter, they are carried tomography computed or tumor sizing and location of the regions of interest (tumor, healthy and critical). Thus, the doctor determines the dose to be applied in the tumor (![]() ).
).
The Image tomography and divided into pixels and are obtained as Geometric Positions of pixels locations relating to tissues Critics, healthy and tumor to be used in doses of Matrix Construction ![]() as defined in (1.3).
as defined in (1.3).
For the computational experiment, it is considered hypothetically, that the patient has a spherical tumor with a diameter of 15 mm, surrounded by critical tissue, exemplifying a spinal cord tumor, where there is difficulty in planning due to cancer was fully surrounded by a critical structure [7] .
In this case, it has been indicated a radiotherapy treatment with tumor dose of 80 Gy, where Gy represents the amount of absorbed ionizing radiation energy (or dose) for mass unit (1 Gray (Gy) = 1 J/kg). It was considered a percentage change![]() , and the critical structure can accommodate up to 40 Gy and healthy at most 60 Gy. As the positive scalar (w) considering the importance that the tumor receives the dose minimum, two values was considered for comparison, namely
, and the critical structure can accommodate up to 40 Gy and healthy at most 60 Gy. As the positive scalar (w) considering the importance that the tumor receives the dose minimum, two values was considered for comparison, namely ![]() and
and![]() . Other bounds are given on the Table 1.
. Other bounds are given on the Table 1.
The considered lesion contains four pixels (2 × 2 pixels), the critical tissue around the lesion comprises 16 pixels (4 × 4 pixels). The developed planning system uses a grid
of 16 × 16 pixels, with 4 angles from 0, ![]() ,
, ![]() and
and ![]() degrees, where each beam is composed by six sub-beams.
degrees, where each beam is composed by six sub-beams.
To improve the computational performance, we have considered only the region that tends to form hot pixels, which are pixels that receive radiation being considered healthy structure with 36 pixels. The pixels that will not receive radiation are called cold pixels [8] .
The 1.5 objective function is the sum of three goals: to achieve a high enough dosage to eliminate the cancer and not exceed the maximum dose in healthy tissues and critical. The Table 2 summarizes the numerical results obtained on the value of the objective function, number of iterations and run time in seconds.
Analyzing the results in Table 2, we can see that the minimized function achieved a very low value, which is a good conformation of isodose curves, thus ensuring a safe
![]()
Table 1. Values in the model relative the doses.
![]()
Table 2. Numerical results in the objective function.
treatment. The dose of excesses in critical and healthy regions and the dose deficit in the tumor region is almost zero, thus showing that the tumor received the dose required for elimination and the dose limit allowed for other regions was not exceeded.
The weight w decides the importance of dose uniformity in the tumor. As we can see the results, if w is small, indicates that finding a treatment plan reach the dose lower limit of the tumor is not so important. Increasing w increases the chances that the treatment plan to reach an uniform dose and tumor need. Thus, higher values for w force excess dose in the tumor to be as minimal as possible.
Compared to the Interior Point Methods
At this moment, we compare the dual simplex method with interior points methods to three real problems.
Analysis report on the results obtained:
In Table 3 and Table 4 the computational time for the dual simplex method is slightly less when compared to the interior point method, unlike what happens with the larger problem 1.5 which is easily explained as the interior point method always has good results for large problems [9] , which does not occur with the Simplex method. In all other aspects the methods have the same performance.
In Table 5 the computational time for the interior point methods is smaller compared to the dual simplex method and this is common with increasing the dimension of the problem, since it is a robust method and very used in large problems.
6. Conclusions
This work presented an application of the simplex method in a cancer treatment plan for radiotherapy and a model based on linear programming for assistance in optimal planning. It can be seen that the mathematical model used in this paper can be a tool of great importance in the construction of optimized treatment plans; it provides a set of optimal solutions, which related to the treatment, may enable a high quality therapy [10] .
It is possible to consider the dual simplex method to ensure reliable treatment of medium and small problems, since their computational cost is lower than the interior point methods, but its performance is very similar.
Acknowledgements
This research was partially sponsored by the Foundation for the Support of Research of the State of São Paulo, (FAPESP) and the Brazilian Council for the Development of Science and Technology (CNPq) and Improvement of Higher Education Personnel (CAPES).