Predictive Elastoplastic Damage Constitutive Law: Establishment of Equivalence Relation between Intrinsic and Extrinsic Material Parameters ()
1. Introduction
The optimization of the forming process by plastic deformation leads to cost savings in manufacturing and improvement of the reliability of the formed parts. Numerical simulation of the mechanical behavior of thin shells is used as tool to predict and evaluate the risks and failures that maybe encountered in the forming process [1] [2] .
The material constitutive law must be able to capture anisotropy, strain hardening, damage evolution and forming limits. Continuum models for hardening plasticity coupled with damage help designers to evaluate manufacturability in the early design stage for mechanical parts production. Most of these models are based on a macroscopic consideration whose formulation is defined within the framework of irreversible thermodynamic processes [3] based on state variables associated with the phenomena under consideration.
Two modeling approaches are currently available in literature for the damage assessment. The first approach is based on the void growth rate inside a phase with elastoplastic behavior [4] [5] . In this approach damage is represented by a scalar representing the void volume fraction; its evolution is linked to the growth of the voids in the material. This evolution occurs in three stages: nucleation of microvoids or microcracks, then coalescence of microcracks into macrocracks and finally crack growth which leads to final failure [6] [7] . In the second approach, a damage variable defined as the relative reduction of the transverse section of an elementary representative volume element is used [8] [9] . This definition for damage allows for the introduction of effective stresses using equivalence principles [10] either by using the equivalent strain energy [4] [5] [11] or the equivalent strain [6] [7] . The principle of equivalent strain states that the strain in the nominal and effective configuration must be the same; whereas the principle of equivalent strain energy states that the elastic strain energy densities are the same for the effective and nominal configurations. In both approaches, damage is defined analytically using constitutive laws able to model the forming process and predict the localized zones of failure [12] [13] [14] [15] [16] .
The development of different procedures for the characterization of constitutive laws of materials through the use of the finite element method [17] [18] [19] was instrumental in the identification of nonlinear constitutive laws with a large number of parameters. The usual continuum mechanics problem consists in determining the parameters of the material model; analytical solutions to such a problem are virtually inexistent except in very special cases. Nevertheless, the identification of parameters of a constitutive law is often treated as an inverse problem. Genetic algorithms and neural networks were used for parameter identification of nonlinear models [20] [21] [22] . The simplex method was used to determine parameters associated with anisotropy of materials in linear problems [23] [24] .
In some cases a combination of methods were used to reach an optimal solution. For the most of these methods, the material parameters were obtained iteratively by minimizing an objective error function involving the constitutive law. The objective function is an expression of the deviation between experimental results and their counterparts obtained through the finite element method [25] [26] ; this objective function may be defined as the square error between the experimental and numerical values at the same points for fields such as elongation and stress [19] [27] etc.
Parameter identification methods available in the literature are based on complex algorithms and time consuming calculation. In most optimization procedures, the uniqueness of the optimal solution is not guaranteed and this may be reflected in the dependence of the optimal solution on the initial guess for the parameters. Furthermore, additional constraints must be added in order to take into account certain physical phenomena that are mathematically impossible to uncouple. Given the complexity of these methods and the size of the experimental data, appropriate computing strategies are necessary.
To the authors’ best knowledge there is no method in the literature which would be able to identify material parameters easily and quickly. The aim of this paper is to pre- sent a new procedure of identifying material model parameters. It deals with establishing a linear relationship between material parameters and shape indexes extracted from the experimental force/elongation (tensile test) curves. This study is limited to the Swift hardening law coupled with an isotropic damage variable.
The idea is to gather materials having an equivalent behavior in the same class according to the shape of their experimental tensile force/elongation response. This is motivated by observing that gathered materials must behave somewhat like a reference material. An equivalence relation is built from a statistical characterization of a material reference and then extends to other materials belonging to this class. The equivalence relation relates the material parameters and shape indexes of experimental tensile force/ elongation curve.
2. Theoretical Development
2.1. Constitutive Laws
In a previous study [28] [29] , an isotropic damage law D was proposed based on the notion of effective stress and apparent stress, an anisotropy using the Hill48 yield criterion and Swift’s isotropic hardening law coupled with the damage variable D. The equivalent stress and damage are given as:
1) Hill’s equivalent stress seq de Hill48 as a function of the anisotropy parameters (F, G, H, N) of the in-plane stresses ,
, 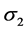 and
and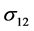 :
:
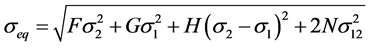 (1)
(1)
2) The damage D as a function of the cumulative equivalent plastic strain eeq:
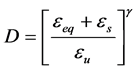 (2)
(2)
where: D is the damage variable specified as 0 £ D £ 1; D = 0 (initial undamaged state), D = 1 (final fractured state); eu is the total cumulated plastic strain up to failure; es is a threshold strain level under which no damage is incurred; g is an exponent that indicates the extent of damage in the material.
3) Swift’s isotropic hardening law coupled with damage expresses the equivalent stress as a function of the equivalent strain through the Equation (3).
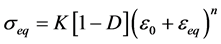 (3)
(3)
In order to characterize the material law three sets of unknowns must be determined:
1) Four anisotropy parameters F, G, H and N in terms of the Lankford coefficients (r0, r45 and r90) are evaluated experimentally [28] .
2) Three parameters from Swift’s hardening law (K, e0, n) where the equivalent yield stress is given in terms of the cumulated equivalent plastic strain as:
 (4)
(4)
3) Three parameters to identify the isotropic ductile damage law g, es and eu.
In this study an original method to identify the last two sets of parameters for hardening and damage is presented.
2.2. Identification Procedure
A procedure of identification by multiple regression is executed in three steps. In the first step data are collected according to a full factorial design. The independent variables consist in virtual material parameters of the constitutive law. Ultimately these material parameters are the target of the identification procedure. For each set of the virtual material parameters, the constitutive law is defined and then implemented in ABAQUS/Standard to simulate a characterization test. The dependent variables are represented by a set of shape indexes extracted from the simulated characterization tests.
In the second step, it comes to establish a relationship by multiple linear regression between material parameters and shape indexes. In fact, multiple regression provides a means to express a dependent variable (z) in terms of f independent variables ( ):
):
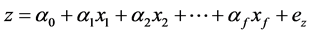 (5)
(5)
where 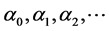 are the regression coefficients with residual error ez.
are the regression coefficients with residual error ez.
In the present study we are interested in the transposed problem stated as follows; given p dependent variables (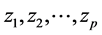 ) and f independent variables (
) and f independent variables (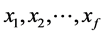 ). For the ith variable xi multiple linear regression leads to a linear equation of the form
). For the ith variable xi multiple linear regression leads to a linear equation of the form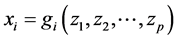 :
:
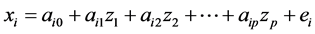 (6)
(6)
This generates a system of f linear equations that can be written in a standard matrix form:
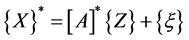 (7)
(7)
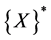 is the unknown vector of the material parameters (independent variables) to be calculated,
is the unknown vector of the material parameters (independent variables) to be calculated, 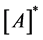 is the regression coefficient matrix,
is the regression coefficient matrix,  is the vector of the shape indexes (dependent variables) and
is the vector of the shape indexes (dependent variables) and ![]() is the residual vector.
is the residual vector.
![]()
![]()
The criteria for the minimization of the residual vector ![]() of the predictive correlations of relation (Equation (7)) is imposed by the hypothesis test of the analysis of variance (ANOVA) such as the coefficient of determination (
of the predictive correlations of relation (Equation (7)) is imposed by the hypothesis test of the analysis of variance (ANOVA) such as the coefficient of determination (![]() ), the adjusted coefficient of determination (
), the adjusted coefficient of determination (![]() ) and the root mean square error (RMSE). Finally the adjusted value
) and the root mean square error (RMSE). Finally the adjusted value ![]() is obtained using Equation (8) with
is obtained using Equation (8) with ![]() the residual between predicted and observed values (9).
the residual between predicted and observed values (9).
![]() (8)
(8)
![]() (9)
(9)
In the third step the material parameters are identified by substituting in the established relation (Equation (8)) the shape indexes extracted from the experimental tensile curves of a reference material.
The accuracy of the identified model is estimated by minimizing the objective functions [30] ![]() and
and![]() , which expresses the discrepancy between the experimentally measured and the numerically computed force and elongation for a set of m points. The average relative errors for the force and elongation from the tensile tests are provided by the Equations (10) and (11) respectively.
, which expresses the discrepancy between the experimentally measured and the numerically computed force and elongation for a set of m points. The average relative errors for the force and elongation from the tensile tests are provided by the Equations (10) and (11) respectively.
![]() (10)
(10)
![]() (11)
(11)
where, Fiexp and Finum are respectively the experimental and calculated tensile force. Uiexp and Uinum are respectively, the experimental and the calculated elongations and m is the total number of experimental points.
2.3. Equivalence Relation and Equivalence Class
Once the identification of the material parameters is successful for the reference material, the relation (12) of the regression coefficent matrix derived from relaion (8) can be written as:
![]() (12)
(12)
where the couple ![]() represents respectively the material parameters and the experimental shape indexes of the reference material; than the “equivalence relation (R)” over the set
represents respectively the material parameters and the experimental shape indexes of the reference material; than the “equivalence relation (R)” over the set ![]() (
(![]() is the set of real numbers) is built between two couples of characteritics as:
is the set of real numbers) is built between two couples of characteritics as:
![]() (13)
(13)
where ![]() represents respectively the material parameters and the experi- mental shape indexes of a new material. The relationship (13) can be expressed as:
represents respectively the material parameters and the experi- mental shape indexes of a new material. The relationship (13) can be expressed as:
![]() (14)
(14)
It is easy to prove that the equality relation R satisfies: the reflexive, symmetric, and transitive properties. The set ![]() is “an equivalence class”.
is “an equivalence class”.
![]() (15)
(15)
So the reference material characterizes by ![]() is considred as a equivalence class. Thereby any other new material, that belongs to this equivalence class shares the same attributes. This is motivated by its behavior that must be similar to that of the reference material. The material parameters verctor {Y} is immediately calculated by the relationships (8). This must be true regardless of the experimental conditions (speed, temperature) of the tensile test.
is considred as a equivalence class. Thereby any other new material, that belongs to this equivalence class shares the same attributes. This is motivated by its behavior that must be similar to that of the reference material. The material parameters verctor {Y} is immediately calculated by the relationships (8). This must be true regardless of the experimental conditions (speed, temperature) of the tensile test.
2.4. Shape Indexes of the Tensile Test Curves
The shape indexes vector ![]() is constituted by the specific points characterizing the tensile force/elongation curve (Figure 1).
is constituted by the specific points characterizing the tensile force/elongation curve (Figure 1).
![]()
Figure 1. Shape indexes of the tensile force/elongation curve.
The points A(dA, FA) and C(dC, FC) correspond, respectively, to the maximum force, the maximum elongation. E(dE, FE) corresponds to the minimum force of the hardening area on the tensile force/elongation curve. After selecting D1, D2 and D3 are tangent lines to the tensile force/elongation curve that pass through the selected points A, C and E. These three tangent lines are plotted on excel to show the bell shaped tensile curve. B(dB, FB) and D(dD, FD) are the intersection points of the tangent lines D1 with D2 and D1 with D3, respectively. The indexes p1(D1), p2(D2) and p3(D3) are the respective slopes of the tangent lines D1, D2 and D3.
3. Experimental Procedure
3.1. Elastoplastic Anisotropic
The standard-steel specified as E24 in accordance with the NF A 35-573/4 (France Standard Structural steel) (United States Equivalent Grades: A283C and European Union Equivalent Grades: S235) is chosen as reference material. It is a structural grade steel with a minimum yield strength which widely used in the engineering and construction industries. With minimum yield strength, E24 structural steel is a common carbon structural steel that can be used in a very broad range of fabrication processes and its plate has excellent formability. It is often favored by the engineer trying to maximize strength or structure while minimizing its weight.
The procedure used to identify the material parameters of the anisotropic elastoplastic behavior coupled to ductile damage of the reference material E24 is described in a previous works [29] . The parameters concerning the anisotropy and the hardening of sheet are given starting from the local rational curves (stress/strain) of the tensile tests for three rolling directions (Figure 2), whereas the global predicted curved (tensile force/elongation) is used obtained to the best plastic stress flow evolutions model representing the behavior of the used material.
The tensile tests were carried out at a strain rate of 10−3 s−1 at room temperature of 25˚C. The tensile tests of the 0˚ oriented specimens were taken as reference. Table 1 presents the anisotropy coefficients of the sheet material E24 determined experimentally using the Lankford coefficients (r0, r45 and r90) [29] .
3.2. Summary of Finite Element Modeling of the Tensile Tests
A three-dimensional finite element analysis (FEA) has been performed using the finite
![]()
Figure 2. Oriented tensile test specimens of standard steel E24 (NF A03-151).
element code ABAQUS/Standard to investigate the tensile test. The imposed boundary conditions on the 0˚ oriented specimens (NF A03-151) include a fixed end on the side of the stationary grip and a uniform displacement on the side of the moving grip. The finite element type “C3D8R” used, are eight-node three-dimensional continuum elements with reduced linear integration; the mesh size is 2391 elements. For a given constitutive law, the numerical model returns the computed response as a tensile force/ elongation curve.
3.3. Building of the Database for Analysis
To build the database for analysis the three steps above are applied on two identification phases: hardening phase and damage phase.
The collected data for hardening phase is made up from a set of simulations based on full factorial design. The independents variables consist in a virtual hardening material parameters (K, ε0, n) of the uncoupled constitutive law (Swift model D = 0; Equation (4)). Table 2 illustrates the values of the levels of the hardening material parameters used to generate the full factorial design P3(33) (where 33 = (levels number)factors number). These levels were chosen within the variability limits of the hardening coefficients observed for steels.
Each combination of the full factorial design is used to implement the uncoupled constitutive law in ABAQUS/Standard to perform simulation of the tensile test. The dependent variables are the shape indexes of the computed tensile force/elongation curve of the simulation test. Eight shape indexes are retained for the identification of the hardening parameters; they are the coordinates of the points A, D and E and the slopes of the tangent lines D1 and D3 (Figure 1). A relationship is built by multiple linear regression for each hardening material parameter in function of the selected shape indexes.
Making use of the shape indexes extracted from the experimental tensile curve, the relationships are used to get the results of the parameter identification of the uncoupled model of the reference material.
![]()
Table 1. Characteristic parameters of standard-steel E24.
![]()
Table 2. Levels used for the hardening coefficients.
The coefficients (K, ε0, n) identified above are treated as constants and used to address the damage phase of identification. The collected data is made up from a new full factorial design P3(33) where the simulations are conducted using the coupled constitutive law (D ≠ 0; Equation (3)). The independents variables consist in a virtual damage material parameters (γ, εs, εu). Table 3 illustrates the values of the levels of the damage material parameters used to generate the full factorial design P3(33); they are chosen in the range available for steels.
Eight other shape indexes are retained for the identification of the damage parameters; they are the coordinates of the points A, B and C and the slopes of the tangent lines D1 and D2. A relationship is built by multiple linear regression for each damage material parameter in function of the new selected shape indexes.
Finally, the shape indexes extracted from the experimental tensile curve are introduced to the relationships to get the results of the parameter identification of the uncoupled model of the reference material.
Figure 3 exposes the identification procedure of the reference material parameters.
![]()
Table 3. Levels used for the damage coefficients.
![]()
Figure 3. Identification procedure of the reference material parameters.
The procedure involves running ABAQUS/Standard from a python script with input from an Excel file which holds the full factorial design. The Excel file can be easily parameterized and analyzed within the Matlab software.
Once results have been validated through both Equations (10) and (11), all materials verifying the equivalence relation (12) belong to the equivalence class ![]() (Equation (15)) constituted by the reference material.
(Equation (15)) constituted by the reference material.
4. Identification Results of Reference Material
4.1. Identification of the Hardening Material Parameters
Twenty seven simulations of tensile test according to the full factorial design P3(33) are run. The different combinations of the virtual hardening parameters are defined in accordance with levels in Table 2. Table 4 shows for each combination introduced to implement the uncoupled constitutive law in ABAQUS, the shape indexes extracted from the computed tensile force/elongation curves.
![]()
Table 4. The full factorial design of the simulation results in hardening case.
As a predictive analysis, the Matlab stepwise linear regression is used to select the most important shape indexes that contribute to the hardening parameter variations. This stepwise method keeps the number of potential variables to a minimum. The coefficients (a1i) of the regression Equation (16) are expressed in Table 5.
![]() (16)
(16)
where xh expresses the hardening parameter (K, e0, n); and (dE, FE, dD, FD, dA, FA, p3, p1) are the hardening shape indexes of the tensile force/elongation graph.
The results show that two shape indexes (![]() ,
,![]() ) do not have any effect on any one of the hardening parameters. It is stated that 99.9%, 94.4% and 95.3% of the variability of K, e0 and n, respectively are explained. These high values of R2 indicate that the models of hardening material parameters have a good fit. K, e0 and n can therefore be identified by introducing the shape indexes obtained from the experimental tensile force/elongation graph (Table 6) in the reduced Equation (17):
) do not have any effect on any one of the hardening parameters. It is stated that 99.9%, 94.4% and 95.3% of the variability of K, e0 and n, respectively are explained. These high values of R2 indicate that the models of hardening material parameters have a good fit. K, e0 and n can therefore be identified by introducing the shape indexes obtained from the experimental tensile force/elongation graph (Table 6) in the reduced Equation (17):
![]() (17)
(17)
The results of the parameter identification are presented in Table 7. In Figure 4, a comparison between the tensile force/elongation graph obtained by simulation with the uncoupled Swift model and the experimental graph for standard-steel E24 tested at
![]()
Table 5. Data analysis results from the P3(33) for the hardening case (standard-steel E24).
![]()
Table 6. Shape indexes of the experimental tensile force/elongation graph of standard-steel E24 (at 25˚C and 10−3 s−1).
![]()
Table 7. Parameter identification results of the hardening parameters of standard-steel E24 at (25˚C and 10−3 s−1).
![]()
Figure 4. Tensile curves: experimental vs. simulated uncoupled Swift Model of standard steel E24 (25˚C and 10−3 s−1).
(25˚C and 10−3 s−1) is presented. The average relative error xF of 0.2% of the hardening portion of the graph (between 0.05 mm and 17 mm) was observed indicating good agreement between the two graphs.
4.2. Identification of the Damage Material Parameters
The hardening material parameters (K = 517.56, ε0 = 1.86, n = 0.242) identified above (Table 7) are used to perform the damage phase of identification. Twenty seven simulations of tensile test according to a new full factorial design P3(33) are run. The different combinations of the virtual damage parameters (γ, εs, εu) are defined in accordance with levels in Table 3. Table 8 shows all combinations introduced to implement the coupled constitutive law (D ≠ 0; Equation (3)) in ABAQUS. It also shows the shape indexes extracted from the damage side of the computed tensile force/elongation curves.
The coefficients (a2i) of the multiple regression Equation (18) are expressed in Table 8.
![]() (18)
(18)
where xd is a damage parameter (es, eu and g); dA, FA, dB, FB, dC, FC, p1 and p2 are the damage shape indexes of the tensile force/elongation graph.
![]()
Table 8. The full factorial design of the simulation results in damage case.
The results of the analysis presented in Table 9 show that the damage threshold parameter es does not depend of the shape indexes. In fact, it may be considered as a parameter intrinsic to the material and related to the initial damage in the sheet metal. However, none of the five shape indexes (FB, dA, FA, p1, p2) has no effect on damage parameters. The coefficients of determination show that the linear regression relations obtained explain 84.6% of the variability in the cumulated total plastic deformation eu(%) and 67% of the variability in the damage index g.
The identification of the damage material parameters eu and g are now achieved by introducing the damage shape indexes, of the experimental tensile force/elongation curve presented in Table 10, in the reduced Equation (19).
![]() (19)
(19)
The identification results of the damage material parameters are presented in Table 11. The tensile force/elongation graph computed using the coupled Swift model is compared to its experimental counterpart for standard-steel E24 in Figure 5. The average relative error xU between the elongations of the two graphs is on the order of 0.34% confirming the accuracy of the predicted response of the identified model.
To recap, the coupled Swift model of standard-steel E24 depicted by the anisotropic elastoplastic behavior coupled to ductile damage of the reference material E24 is described by the constitutive model (Equation (20)). The material parameters are identified above (Table 7 and Table 11).
![]()
Table 9. Data analysis results from the P3(33) for the damage case (standard-steel E24).
![]()
Table 10. Experimental values of the shape indexes to characterize damage of standard-steel E24 at (10−3 s−1 and 25˚C).
![]()
Table 11. Damage parameter identification results for standard-steel E24 at (25˚C and 10−3 s−1).
![]() (20)
(20)
In Figure 6, it presented the simulation result of the tensile force/elongation of the standard-steel E24. It shows the cumulated plastic equivalent strain fields and the Mises stress obtained from the numerical simulation. For elongations below 17 mm the cumulated plastic deformation as well as damage remained homogenous over the active region of the specimen. Beyond this limit the deformation becomes non-uniform and starts to localize in the middle section of the specimen when elongation reaches 21 mm. Local necking is observed in the form of a shear band signaling the imminent initiation of a macroscopic crack. The agreement between the experimental observations and the identified model confirm the reliability of the proposed parameter identification procedure.
![]()
Figure 5. Tensile curves: experimental vs. simulated coupled Swift Model of standard-steel E24 (25˚C and 10−3 s−1).
![]()
Figure 6. Plastic equivalent strain and Mises stress fields for the coupled Swift model of standard-steel E24.
4.3. Determination of the Equivalence Class
The material parameters of the reference material are now identified this means that the equivalence class {S} is now defined. For any other material whose the couple of parameters (![]() ) is in accordance with Equation (14) belongs to the equivalence class {S}. This means that the material has a behavior partially similar to the reference material and is submitted to the same constitutive model. The material parameters {Y} can be identified immediately by the Equation (21) which substitutes the Equation (8).
) is in accordance with Equation (14) belongs to the equivalence class {S}. This means that the material has a behavior partially similar to the reference material and is submitted to the same constitutive model. The material parameters {Y} can be identified immediately by the Equation (21) which substitutes the Equation (8).
![]() (21)
(21)
Based on Equation (17) and Equation (19) the matrix [A], where all values are extracted from Table 5 and Table 9, is defined as:
![]()
5. Validation and Discussion
The validation of this technique has been extended is extended to the identification of the coefficients of the coupled Swift model of:
1) The behavior of standard-steel E24 under other conditions of temperature and strain rate
2) The behavior in tension of a material with characteristics different from standard-steel E24 such as 1050A aluminum.
5.1. Characterization of Standard-Steel E24 at 1.66 × 10−1 s−1 Strain Rate
The first implementation of this method is concerned with a tensile test of standard- steel E24 at a temperature of 25˚C and a strain rate of 1.66 × 10−3 s−1. Figure 7 shows the initiation of hardening; both graphs have similar features.
The experimental shape indexes from the tensile force/elongation graph are presented in Table 12. They are introduced in Equation (20) to calculate immediately the material parameters according to the coupled Swift model (Table 13).
![]()
Figure 7. Comparison of the tensile curves of standard-steel E24 at different strain rates.
![]()
Table 12. Experimental values of the shape indexes of standard-steel E24 at (1.66 × 10−3 s−1 and 25˚C).
![]()
Table 13. Identification of parameters for standard-steel E24 at (1.66 × 10−3 s−1 25˚C).
Figure 8 presents a comparison between the computed response using the coupled Swift model and the experimental response; the average relative error xF between the two responses is about 0.33% for elongations between 5.2 mm and 17.0 mm. The average relative error xU for elongations between 17.0 mm and 23.0 mm is about 0.34%. For elongations below 5.2 mm a difference exists which seems to be affected by the experimental shape indexes due to uncertainty in the coordinates of point A as well as the slope p1 of the tangent line D1.
5.2. Characterization of Standard-Steel E24 at High Temperature
The second application of the method is concerned with a tensile test of standard-steel E24 at 200˚C and a strain rate of 1.66 × 10−3 s−1. Figure 9 shows an acceptable level of agreement with the tensile graph of the reference test (standard-steel E24 at 25˚C and 10−3 s−1); this makes it possible to identify the hardening and damage parameters directly for the tensile test of standard-steel E24 at 200˚C. The experimental shape indexes are presented in Table 14.
![]()
Figure 8. Tensile graphs of standard-steel E24: experimental (1.66 × 10−3/s) vs. simulated (coupled Swift model).
![]()
Figure 9. Experimental tensile graphs of standard-steel E24 under different conditions.
The results of the identification of hardening and damage parameters by multiple regression at a temperature of 200˚C are presented in Table 15. Figure 10 shows that below an elongation of 4.4 mm the experimental and simulated results display a difference. The average relative difference xF between the two responses is 0.22% for elongations below 14.6 mm whereas for elongations in the range 14.4 mm to 19.1 mm the average relative error xU is about 0.10%.
![]()
Table 14. Experimental shape indexes of the standard-steel E24 at (200˚C and 1.66 × 10−3 s−1).
![]()
Table 15. Identification of parameters standard-steel E24 at (200˚C and 1.66 × 10−3 s−1).
![]()
Figure 10. Tensile curve of standard-steel E24: experimental (200˚C) vs. simulated (with coupled Swift model).
5.3. Characterization of 1050A Aluminum
The third application is concerned with annealed 1050A aluminum. This alloy has good plastic deformation properties. Figure 11 shows the tensile curves of the reference material standard-steel E24 and that of 1050A aluminum; they exhibit a significant geometric similarity. The shape indexes obtained from the experimental tensile force/ elongation graph of 1050A aluminum presented in Table 16; they are used to determine the parameters of the coupled Swift hardening model (Table 17).
Figure 12 shows that the computed response from identified model of Table 17 and the experimental response have an average error xF = 0.38% in the elongation range between 0.05 mm and 23.7 mm and xU = 0.25% for elongation in the range 23.7 mm to 33.1 mm.
![]()
Figure 11. Similarity of the tensile graphs of standard-steel E24 and 1050A aluminum.
![]()
Table 16. Experimental shape indexes of aluminum 1050A (25˚C; 1.66 × 10−3 s−1).
6. Conclusions
The presented work demonstrates the possibilities available through the multiple regression method to the parameter identification problem. The procedure was proven to be efficient in determining the parameters of the Swift hardening model coupled with an isotropic damage variable.
Once the relationship between the material parameters and the shape indexes of the reference material is carried out, it will be used to identify directly the material behavior for a class of materials having the same attributes.
However the extended use of these results to other materials under different test conditions requires their behavior similarity. Hence, the materials may be grouped into equivalence classes according to the shape of their experimental response.
This method provides significant gains in computer time necessary for a complete identification procedure for the reference material. It needs very few simulations compared to other identification methods. However it just needs only one simulation for the identification of similar behavior.
Future efforts will be directed to:
1) Introduction on nondimensional variable in the analysis which will broaden the utility range of the correlations.
![]()
Table 17. Identification of parameters for aluminum 1050A (25˚C; 1.66 × 10−3 s−1).
![]()
Figure 12. Tensile graphs of aluminum 1050A: Experimental vs. simulated response (coupled Swift model).
2) Generalization to constitutive models which have a large number of parameters.
3) Sensitivity analysis of the parameter to identify with respect to the shape indexes.