A Class of Lindley and Weibull Distributions

Said Hofan Alkarni

Department of Quantitative Analysis, King Saud University, Riyadh, Saudi Arabia.

DOI: 10.4236/ojs.2016.64058                

Abstract

In this paper, we introduce a class of Lindley and Weibull distributions (LW) that are useful for modeling lifetime data with a comprehensive mathematical treatment. The new class of generated distributions includes some well-known distributions, such as exponential, gamma, Weibull, Lindley, inverse gamma, inverse Weibull, inverse Lindley, and others. We provide closed-form expressions for the density, cumulative distribution, survival function, hazard rate function, moments, moments generating function, quantile, and stochastic orderings. Moreover, we discuss maximum likelihood estimation and the algorithm for computing the parameters estimates. Some sub models are discussed as an illustration with real data sets to show the flexibility of this class.

Keywords

Class of Lindley and Weibull Distributions, Lindley Distributions, Weibull Distributions

Received 10 July 2016; accepted 26 August 2016; published 29 August 2016

1. Introduction

The remainder of this paper is organized as follows: In Section 2, we define the class of Lindley and Weibull (LW) distributions and show that many existing distributions belong to this class. The LW properties, such as survival function, hazard rate function, moments, moment generating function, quantile, and stochastic orderings, are discussed in Section 3. In Section 4, some special cases of the LW class are introduced to show the flexibility of this class in generating existing distributions. Section 5 contains the maximum likelihood estimates of the LW class and the relevant asymptotic confidence interval. Two real data sets are introduced in Section 6 to show the applicability of the LW class. In Section 7, we introduce a conclusion to summarize the contribution of this paper.

2. The Class of Lindley and Weibull Distributions

In this section, we introduce simple forms of cumulative distribution function (cdf) and probability distribution function (pdf) for the LW class.

Definition. Let 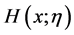be a non-negative monotonically increasing function that depends on a

nonnegative parameter vector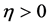, we define the cdf for any random variable of the LW class to be

(1)

The corresponding pdf becomes

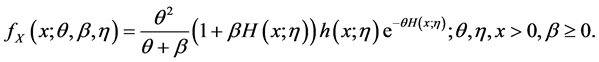(2)

And for 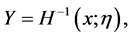the cdf and pdf of LW become

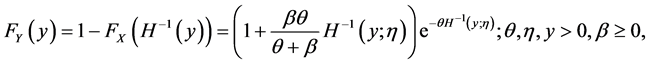(3)

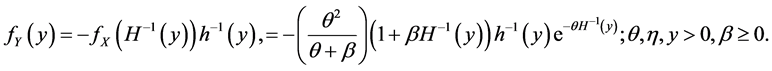(4)

Many Lindley types and Weibull types of distributions are members of the LW class, depending on the choice of the function 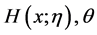and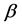. Some examples are listed in Table 1.

The pdf(2) can be shown as a mixture of two distributions, as follows:

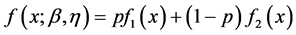
where

. The shape and the mode location of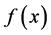

depend on the type of.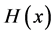

3. General Properties

3.1. Survival and Hazard Functions

For any non-decreasing function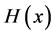, the survival function (sf) is given by

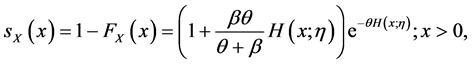(5)

and the associate hazard rate function is given by

(6)

For the survival and hazard rate functions are given, respectively, by

(7)

and

Table 1. Some existing distributions as examples of the LW class.

(8)

3.2. Moments and Moment Generating Function

The moments and the moments generating function (mgf) for an LW class can be obtained by direct integration as follows:

.

Using the series expansion the above expression is reduced to

As a special case, if we let then

(9)

(10)

and, hence, the mean and the variance are

(11)

(12)

For then

(13)

(14)

The mean and the variance, then, are

(15)

. (16)

3.3. Quantile and Stochastic Orderings

Theorem 1. Let X be a random variable with pdf as in (2), the quantile function, say is

where, and is the negative Lambert W function.

Proof: We have, which implies, so, by substitution, we get

, raising both sides to and multiplying by

, we have the negative Lambert equation,

. Solving this equation for, the proof

is complete.

Note that one can use the same proof above to obtain

Stochastic ordering of positive continuous random variables is an important tool for judging the comparative behavior. A random variable X is said to be smaller than a random variable Y in the following contests:

1) Stochastic order

2) Hazard rate order

3) Mean residual life order

4) Likelihood ratio order

The following implications (Shaked & Shanthikumar, [18] ) are well known in that

The following theorem shows that all members of the LW class are ordered with respect to “likelihood ratio” ordering.

Theorem 2. Suppose then

1) If and, hence,

2) If and, hence,

Proof. We have

,

and

Thus,

Case 1) If

then This means that and, hence,

Case 2) If, then

This means that and, hence,

4. Special Cases

4.1. Lindley Distribution

The original Lindley distribution (L), proposed by Lindley [12] , is a special case of LW class, with and. Using (1), the cdf of the Lindley distribution is given by

The associated pdf using (2) is given by

It can be seen that this distribution is a mixture of exponential and gamma distributions. According to forms (5) and (6), the corresponding sf and hrf are given respectively by

and

A direct substitution in (9) and (10), with, gives us the moments and mgf for the Lindley distribution:

The mean and the variance from (11) and (12) are

Figure 1 displays the plots of density and hazard rate function of the Lindley distribution.

4.2. Power Lindley Distribution

Power Lindley distribution (PL), introduced by Ghitany et al. [14] , is a special case of LW class with

Figure 1. Plots of the pdf and hrf of the Lindley distribution for different values of.

and. Using the cdf form in (1), the cdf of PL distribution is given by

The associated pdf using (2) is given by

The PL distribution is a mixture distribution of the Weibull distribution (with shape parameters and scale) and a generalized gamma distribution (with shape parameters and scale), with mixing proportion

The sf and hrf of the PL distribution are obtained from (5) and (6),

Figure 2 shows the pdf and hrf of the PL distribution of some selected choices of and.The row moment and the mgf of the PL distribution, using (9) and (10), are given, respectively, by

Therefore, the mean and the variance of PL distribution are obtained by direct substitution in (11) and (12),

Figure 2. The pdf and hrf of the PL distribution for some selected choices of and.

4.3. Extended Power Lindley Distribution

Extended power Lindley distribution (EPL), introduced by Alkarni [3] , is a special case of LW class with. Using the cdf form in (1), the cdf of the EPL distribution is given by

The associated pdf using (2) is given by

We see that the EPL is a two-component mixture of the Weibull distribution (with shape and scale) and a generalized gamma distribution (with shape parameters and scale), with mixing proportion.

The sf and hrf of the EPL distribution are obtained as a direct substitution in (5) and (6),

Figure 3 shows the pdf and hrf of the EPL distribution for some choices of, and.The row moment and the mgf of the EPL distribution, using (9) and (10), are given, respectively, by

Using (11) and (12), the mean and the variance of the EPL distribution are given, respectively, by

Figure 3. The pdf and hrf of the EPL distribution for some choices of, and.

4.4. Inverse Lindley Distribution

Inverse Lindley (IL) distribution, proposed by Sharma et al. [13] , is a special case of the LW class with and. Using the cdf form in (3), the cdf of the IL distribution is given by

The associated pdf using (4) is given by

We see that the IL is a two-component mixture of the Weibull distribution (with shape and scale) and a gen- eralized gamma distribution (with shape parameters and scale), with mixing proportion.

The sf and hrf of the IL distribution are obtained as a direct substitution in (7) and (8),

Figure 4 shows the pdf and hrf of the IL distribution for some choices of

4.5. The Generalized Inverse Lindley Distribution

The generalized inverse Lindley (GIL) distribution, proposed by Sharma et al. [15] , is a special case of LW class with and. Using the cdf form in (3), the cdf of the GIL is given by

Figure 4. The pdf and hrf of the IL distribution for some selected choices of.

The associate pdf, using (4), is given by

The associate hrf, using (8), is given by

Figure 5 shows the pdf and hrf of the GIL distribution of some selected choices of and.The row moment of the generalized inverse Lindley distribution, using (10), is given by

The mean and the variance of the generalized inverse Lindley distribution are given, respectively, by

4.6. Extended Inverse Lindley Distribution

The extended inverse Lindley (EIL) distribution, proposed by Alkarni [17] , is a special case of the LW class with. Using the cdf form in (3), the cdf of the EIL distribution is given by

Figure 5. The pdf and hrf of the GIL distribution for some selected choices of and.

The associated pdf, using (4), is given by

We see that the EIL is a two-component mixture of the inverse Weibull distribution (with shape and scale) and a generalized inverse gamma distribution (with shape parameters and scale), with the mixing proportion.

The hrf of the EIL distribution is given by

Figure 6 shows the pdf and hrf of the EIL distribution for some choices of, and.The row moment of the EIL distribution, using (9), is given by

Therefore, the mean and the variance of the EIL distribution are given, respectively, by

5. Estimation and Inference

Let be a random sample, with observed values from the LW class with parameters. Let be the parameter vector. The log likelihood function is given by

Figure 6. The pdf and hrf of the EIL distribution for some choices of, and.

,

then the score function is given by

where

The maximum likelihood estimation (MLE) of says is obtained by solving the nonlinear system. This nonlinear system of equations does not have a closed form. For interval estimation and hypothesis tests on the model parameters, we require the observed information matrix

,

where the elements of are the second partial derivatives of. Under standard regular conditions for large sample approximation (Cox and Hinkley, [19] ) that fulfilled for the proposed model, the distribution of approximately with Whenever the parameters are in the interior

of the parameter space but not on the boundary, the asymptotic distribution of is where is the unit information matrix and p is the number of parameters of the distribution. The asymptotic multivariate normal distribution of can be used to approximate con-

fidence interval for the parameters and for the hazard rate and survival functions. An asymptoticconfidence interval for parameter is given by

where is the diagonal element of for and is the quantile of the

standard normal distribution.

6. Applications

In this section, we introduce two data sets as applications of the LW class. For the first data set, we fit L, PL, and EPL models as well as the Two-parameter Lindley (TL) and the standard Weibull (W).

The first data set was introduced by Bader and Priest [20] as the tensile strength measurements on 1000 carbon fiber-impregnated tows at four different gauge lengths. The data is listed in Table 2.

The MLEs of the parameters were obtained using the expectation-maximization (EM) algorithm. The MLEs, Kolmogorov-Smirnov statistic (K-S) with its respective p-value, the maximized log likelihood for the above distributions are listed in Table 3. The distributions are ordered in the table according to their performance. The fitted densities and the empirical distribution versus the fitted cumulative distributions of all models for this data are shown in Figure 7 and Figure 8, respectively.

Table 2. Carbon fiber tensile strength.

Table 3. Parameter estimates, K-S statistic, p-value, and logL of carbon fiber tensile strength.

Figure 7. Plot showing the fitted densities of the models listed in Table 3.

For the second data set, we demonstrate the applicability of the IL, GIL, and EIL, as well as the inverse Weibull (IW) and the generalized inverse Weibull (GIW) models. Table 4 represents the flood levels for the Susquehanna River at Harrisburg, Pennsylvania, over 20 four-year periods from 1890 to 1969. This data has been used by several authors and was initially reported by Dumonceaux & Antle [21] .

The MLEs of the parameters, the Kolmogorov-Smirnov statistic (K-S) with its respective p-value, and the maximized log likelihood (logL) for the above distributions are given in Table 5 according to their performance. The fitted densities and the empirical distribution versus the fitted cumulative distributions of all models for this data are shown in Figure 9 and Figure 10, respectively.

7. Concluding Remarks

We define a new family of lifetime distributions, called the LW family of distributions, that generates Lindley and Weibull distributions. The LW class contains many lifetime subclasses and distributions. Various standard mathematical properties were derived, such as density and survival hazard functions, moments, moment generating function, and quantile function, and were introduced in flexible and useful forms. The maximum likelihood

Figure 8. Plot showing the fitted cdfs of the models listed in Table 3.

Figure 9. Plot showing the fitted densities of the models listed in Table 5.

Figure 10. Plot showing the fitted cdfs of the models listed in Table 5.

Table 4. Flood level data for the Susquehanna River.

Table 5. Parameter estimates, KS statistic, P-Value, and logL of flood level data.

method was used for parameter estimation using the EM algorithm. Finally, some special models were introduced and fitted to real datasets to show the flexibility and the benefits of the proposed class.

Acknowledgements

The author is highly grateful to the Deanship of Scientific Research at King Saud University, represented by the Research Center at the College of Business Administration, for supporting this research financially.

Competing Interests

The author declares that there were no competing interests.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bagheri, S., Bahrami, E. and Ganjali, M. (2016) The Generalized Modified Weibull Power Series Distribution: Theory and Applications. Computational Statistics and Data Analysis, 94, 136-160. http://dx.doi.org/10.1016/j.csda.2015.08.008
[2]	Ghitany, M., Atieh, B. and Nadadrajah, S. (2008) Lindley Distribution and Its Applications. Mathematics and Computers in Simulation, 78, 493-506. http://dx.doi.org/10.1016/j.matcom.2007.06.007
[3]	Alkarni, S. (2015) Extended Power Lindley Distribution: A New Statistical Model for Non-Monotone Survival Data. European Journal of Statistics and Probability, 3, 19-34.
[4]	Johnson, N., Kotz, S. and Balakrishnan, N. (1994) Continuous Univariate Distribution, Volume 1. Wiley, New York.
[5]	Rayleigh, J. (1880) On the Result of a Large Number of Vibrations of the Same Pitch and of Arbitrary Phase. Philosophical Magazine, 10, 73-78. http://dx.doi.org/10.1080/14786448008626893
[6]	Lai, C., Xie, M. and Murthy, D. (2003) A Modified Weibull Distribution. IEEE Transactions on Reliability, 52, 7-33. http://dx.doi.org/10.1109/TR.2002.805788
[7]	Xie, M., Tang, Y. and Goh, T. (2002) A Modified Weibull Extension with Bathtub-Shaped Failure Rate Function. Reliability Engineering and System Safety, 76, 279-285. http://dx.doi.org/10.1016/S0951-8320(02)00022-4
[8]	Gompertz, B. (1825) On the Nature of the Function Expressive of the Law of Human Mortality and on a New Mode of Determining Life Contingencies. Philosophical Transactions of the Royal Society, 115, 513-585. http://dx.doi.org/10.1098/rstl.1825.0026
[9]	Smith, R. and Bain, L. (1975) An Exponential Power Life-Testing Distribution. Communications in Statistics-Theory and Methods, 4, 469-481. http://dx.doi.org/10.1080/03610927508827263
[10]	Chen, Z. (2000) A New Two-Parameter Lifetime Distribution with Bathtub Shape or Increasing Failure Rate Function. Statistics and Probability Letters, 49, 155-161. http://dx.doi.org/10.1016/S0167-7152(00)00044-4
[11]	Pham, H. (2002) A Vtub-Shape Hazard Rate Function with Applications to System Safety. International Journal of Reliability and Applications, 3, 1-16.
[12]	Lindley, D. (1958) Fiducial Distributions and Bays Theorem. Journal of the Royal Statistical Society, 20, 102-107.
[13]	Sharma, V., Singh, S., Singh, U. and Agiwal, V. (2015) The Inverse Lindley Distribution: A Stress-Strength Reliability Model. Journal of Industrial and Production Engineering, 32, 162-173. http://dx.doi.org/10.1080/21681015.2015.1025901
[14]	Ghitany, M., Al-Mutairi, D., Balakrishnan, N. and Al-Enezi, I. (2013) Power Lindley Distribution and Associated Inference. Computational Statistics and Data Analysis, 64, 20-33. http://dx.doi.org/10.1016/j.csda.2013.02.026
[15]	Sharma, V., Singh, S., Singh, U. and Merovci, F. (2015) The Generalized Inverse Lindley Distribution: A New Inverse Statistical Model for the Study of Upside-Down Bathtub Survival Data. Communications in Statistics-Theory and Methods, Preprint.
[16]	Shanker, R., Sharma, S. and Shanker, R. (2013) A Two-Parameter Lindley Distribution for Modeling WAITING and Survival Time Series Data. Applied Mathematics, 4, 363-368. http://dx.doi.org/10.4236/am.2013.42056
[17]	Alkarni, S. (2015) Extended Inverse Lindley Distribution: Properties and Application. SpringerPlus, 4, 1-17. http://dx.doi.org/10.1186/s40064-015-1489-2
[18]	Shaked, M. and Shanthikumar, J. (1994) Stochastic Orders and Their Applications. Academic Press, New York.
[19]	Cox, D. and Hinkley, D. (1974) Theoretical Statistics. Chapman and Hall, London. http://dx.doi.org/10.1007/978-1-4899-2887-0
[20]	Bader, M. and Priest, A. (1982) Statistical Aspects of Fiber and Bundle Strength in Hybrid Composites. In: Hayashi, T., Kawata, S. and Umekawa, S., Eds., Progress in Science and Engineering Composites, ICCM-IV, Tokyo, 1129-1136.
[21]	Dumonceaux, R. and Antle, C. (1973) Discrimination between the Lognormal and Weibull Distribution. Technometrics, 15, 923-926. http://dx.doi.org/10.1080/00401706.1973.10489124