Log-Concavity of Centered Polygonal Figurate Number Sequences

Fekadu Tolessa Gedefa

Department of Mathematics, Ambo University, Ambo, Ethiopia.

DOI: 10.4236/oalib.1102774                

Abstract

This paper investigates the log-concavity of the centered m-gonal figurate number sequences. The author proves that for m≥3, the sequence {C_n(m)}_n≥1 of centered m-gonal figurate numbers is a log-concave.

Keywords

Log-Concavity, Figurate Numbers, Centered Polygonal, Number Sequences

Subject Areas: Discrete Mathematics, Combinatorial Sequences, Recurrences

1. Introduction

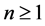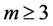For and, let 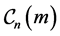denote the 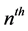term of the centered m-gonal figurate number sequence. E. Deza and M. Deza [1] stated that 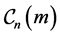could be defined by the following recurrence relation:

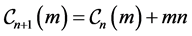(1)

where. E. Deza and M. Deza [1] also gave different properties of and obtained

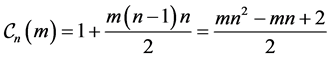(2)

where 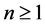and. For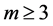, some terms of the sequence 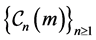are as follows:

Some scholars have been studying the log-concavity (or log-convexity) of different numbers sequences such as Fibonacci & Hyperfibonacci numbers, Lucas & Hyperlucas numbers, Bell numbers, Hyperpell numbers, Motzkin numbers, Fine numbers, Franel numbers of order 3 & 4, Apéry numbers, Large Schröder numbers, Central Delannoy numbers, Catalan-Larcombe-French numbers sequences, and so on (see for instance [2] - [9] ).

To the best of the author’s knowledge, among all the aforementioned works on the log-concavity and log- convexity of number sequences, no one has studied the log-concavity (or log-convexity) of centered m-gonal figurate number sequences. In [1] [10] [11] , some properties of centered figurate numbers are given. The main aim of this paper is to discuss properties related to the sequence. Now we recall some definitions involved in this paper.

Definition 1. Let be a sequence of positive numbers. If for all, , the sequence is called log-concave.

Definition 2. Let be a sequence of positive numbers. If for all, , the sequence is called log-convex. In case of equality, , we call the sequence geometric or log-straight.

Definition 3. Let be a sequence of positive numbers. The sequence is log-concave (log- convex) if and only if its quotient sequence is non-increasing (non-decreasing).

Log-concavity and log-convexity are important properties of combinatorial sequences and they play a crucial role in many fields, for instance economics, probability, mathematical biology, quantum physics and white noise theory [2] [12] - [18] .

2. Log-Concavity of Centered m-gonal Figurate Number Sequences

In this section, we state and prove the main results of this paper.

Theorem 4. For and, the following recurrence formulas for centered m-gonal number sequences hold:

(3)

with the initial conditions and the recurrence of its quotient sequence is given by

(4)

with the initial condition.

Proof. By (1), we have

(5)

It follows that

(6)

Rewriting (5) and (6) for, we have

(7)

(8)

Multiplying (7) by and (8) by, and subtracting as to cancel the non homogeneous part, one can obtain the homogeneous second-order linear recurrence for:

(9)

By denoting

and

one can obtain

(10)

with given initial conditions and.

By dividing (10) through by, one can also get the recurrence of its quotient sequence as

(11)

with initial condition □

Lemma 5. For the centered m-gonal figurate number sequence, let for and. Then we have for.

Proof. Assume for and. Otherwise,

(12)

It follows that which not true. Now it is clear that and

(13)

Assume that for all. It follows from (11) that

(14)

For, by (14), we have

(15)

(16)

(17)

Hence for and

Similarly, it is known that

(18)

Assume that for all. It follows from (11) that

(19)

For, by (19), we have

(20)

(21)

Hence for and □

Thus, in general, from the above two cases it follows that for and.

Lemma 6. For the centered m-gonal figurate number sequence, the quotient sequence, given in (4), is a decreasing sequence for.

Proof. Let be a quotient sequence given in (4). We prove by induction that the sequence is decreasing. Indeed, since, we have. Next we assume that.

By using (11), one can obtain

(22)

with initial condition.

For, by (22), we get

(23)

(24)

(25)

(26)

(27)

By Lemma 5 and induction assumption, one can get for

Thus, the sequence is decreasing for □

Theorem 7 For, the sequence of centered m-gonal figurate numbers is a log-concave.

Proof. Let be a sequence of centered m-gonal figurate numbers and its quotient sequence, given by (4). To prove the log-concavity of for all, it suffices to show that the quotient sequence is decreasing.

By Lemma 6, the quotient sequence is decreasing. Thus, by definition 3, the sequence of centered m-gonal figurate numbers is a log-concave for This completes the proof of the theorem. □

3. Conclusion

In this paper, we have discussed the log-behavior of centered m-gonal figurate number sequences. We have also proved that for, the sequence of centered m-gonal figurate numbers is a log-concave.

Acknowledgements

The author is grateful to the anonymous referees for their valuable comments and suggestions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Deza, E. and Deza, M. (2012) Figurate Numbers. World Scientific.
[2]	Ahmiaab, M., Belbachirb, H. and Belkhirb, A. (2014) The Log-Concavity and Log-Convexity Properties Associated to Hyperpell and Hyperpell-Lucas Sequences. Annales Mathematicae et Informaticae, 43, 3-12.
[3]	Aigner, M. (1998) Motzkin Numbers. European Journal of Combinatorics, 19, 663-675. http://dx.doi.org/10.1006/eujc.1998.0235
[4]	Deutsch, E. and Shapiro, L. (2001) A Survey of the Fine Numbers. Discrete Mathematics, 241, 241-265. http://dx.doi.org/10.1016/S0012-365X(01)00121-2
[5]	Gessel, I. (1982) Some Congruences for Apéry Numbers. Journal of Number Theory, 14, 362-368. http://dx.doi.org/10.1016/0022-314X(82)90071-3
[6]	Santana, S.F. and Diaz-Barrero, J. (2006) Some Properties of Sums Involving Pell Numbers. Missouri Journal of Mathematical Sciences, 18, 33-40.
[7]	Sun, Z.-W. (2011) On Delannoy Numbers and Schröder Numbers. Journal of Number Theory, 131, 2387-2397. http://dx.doi.org/10.1016/j.jnt.2011.06.005
[8]	Sun, Z.-W. (2013) Congruences for Franel Numbers. Advances in Applied Mathematics, 51, 524-535. http://dx.doi.org/10.1016/j.aam.2013.06.004
[9]	Sloane, N.J., et al. (2003) The On-Line Encyclopedia of Integer Sequences.
[10]	Hartman, J. (1976) Figurate Numbers. The Mathematics Teacher, 69, 47-50.
[11]	Weaver, C. (1974) Figurate Numbers. Mathematics Teacher, 67, 661-666.
[12]	Asai, N., Kubo, I. and Kuo, H.-H. (2001) Roles of Log-Concavity, Log-Convexity, and Growth Order in White Noise Analysis. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 4, 59-84. http://dx.doi.org/10.1142/S0219025701000498
[13]	Asai, N., Kubo, I. and Kuo, H.-H. (1999) Bell Numbers, Log-Concavity, and Log-Convexity.
[14]	Došlic, T. (2005) Log-Balanced Combinatorial Sequences. International Journal of Mathematics and Mathematical Sciences, 2005, 507-522. http://dx.doi.org/10.1155/IJMMS.2005.507
[15]	Liu, L.L. and Wang, Y. (2007) On the Log-Convexity of Combinatorial Sequences. Advances in Applied Mathematics, 39, 453-476. http://dx.doi.org/10.1016/j.aam.2006.11.002
[16]	Wang, Y. and Yeh, Y.-N. (2007) Log-Concavity and Lc-Positivity. Journal of Combinatorial Theory, Series A, 114, 195-210.
[17]	Zhao, F.-Z. (2014) The Log-Behavior of the Catalan-Larcombe-French Sequence. International Journal of Number Theory, 10, 177-182.
[18]	Zheng, L.-N., Liu, R. and Zhao, F.-Z. (2014) On the Log-Concavity of the Hyperfibonacci Numbers and the Hyperlucas Numbers. Journal of Integer Sequences, 17, 3.