Weak Insertion of a Continuous Function between Two Comparable α-Continuous (C-Continuous) Functions

Majid Mirmiran

Department of Mathematics, University of Isfahan, Isfahan, Iran.

DOI: 10.4236/oalib.1102453                

Abstract

A sufficient condition in terms of lower cut sets is given for the insertion of a continuous function between two comparable real-valued functions.

Keywords

Weak Insertion, Strong Binary Relation, C-Open Set, Semi-Preopen Set, α-Open Set, Lower Cut Set

Subject Areas: Topology

1. Introduction

The concept of a C-open set in a topological space was introduced by E. Hatir, T. Noiri and S. Yksel in 1996 [1] . The authors define a set s to be a C-open set if, where u is open and A is semi-preclosed. A set s is a C-closed set if its complement is C-open set or equivalently if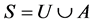, where u is closed and A is semi-preopen. The authors show that a subset of a topological space is open if and only if it is an α-open set and a C-open set. This enable them to provide the following decomposition of continuity: a function is continuous if and only if it is α-continuous and C-continuous.

Recall that a subset A of a topological space 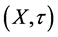is called α-open if A is the difference of an open and a nowhere dense subset of X. A set A is called α-closed if its complement is α-open or equivalently if A is union of a closed and a nowhere dense set. Sets which are dense in some regular closed subspace are called semi-preopen or β-open. A set is semi-preclosed or β-closed if its complement is semi-preopen or β-open.

The concept of a set A was β-open if and only if 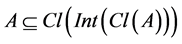was introduced by J. Dontchev in 1998 [2] .

Recall that a real-valued function f defined on a topological space x was called A-continuous if the preimage of every open subset of belongs to A, where A was a collection of subset of x and this the concept was introduced by M. Przemski in 1993 [3] . Most of the definitions of function used throughout this paper are consequences of the definition of A-continuity. However, for unknown concepts, the reader might refer to papers introduced by J. Dontchev in 1995 [4] , M. Ganster and I. Reilly in 1990 [5] .

Hence, a real-valued function f defined on a topological space x is called c-continuous (resp. α-continuous) if the preimage of every open subset of 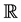is c-open (resp. α-open) subset of x.

Results of Katĕtov in 1951 [6] and in 1953 [7] concerning binary relations and the concept of an indefinite lower cut set for a real-valued function, which was due to Brooks in 1971 [8] , were used in order to give necessary and sufficient conditions for the strong insertion of a continuous function between two comparable real-valued functions.

If g and f are real-valued functions defined on a space X, we write 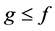in case 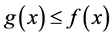for all x in X.

The following definitions were modifications of conditions considered in paper introduced by E. Lane in 1976 [9] .

A property p defined relative to a real-valued function on a topological space is a c-property provided that any constant function has property p and provided that the sum of a function with property p and any continuous function also has property p. If and 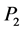are c-property, the following terminology is used: A space x has the weak c-insertion property for 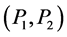if and only if for any functions g and f on x such that 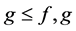has property 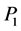and f has property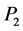, then there exists a continuous function h such that.

In this paper, it is given a sufficient condition for the weak c-insertion property. Also several insertion theorems are obtained as corollaries of this result.

2. The Main Result

Before giving a sufficient condition for insertability of a continuous function, the necessary definitions and terminology are stated.

Let be a topological space, the family of all α-open, α-closed, C-open and C-closed will be denoted by, , and, respectively.

Definition 2.1. Let a be a subset of a topological space. Respectively, we define the α-closure, α-interior, C-closure and C-interior of a set a, denoted by and as follows:

Respectively, we have are α-closed, semi-preclosed and are α-open, semi-preopen.

The following first two definitions are modifications of conditions considered in [6] [7] .

Definition 2.2. If ρ is a binary relation in a set S then is defined as follows: if and only if implies and implies for any u and v in S.

Definition 2.3. A binary relation ρ in the power set of a topological space x is called a strong binary relation in in case ρ satisfies each of the following conditions:

1) If for any and for any, then there exists a set C in such that and for any and any.

2) If, then.

3) If, then and.

The concept of a lower indefinite cut set for a real-valued function was defined [8] as follows:

Definition 2.4. If f is a real-valued function defined on a space x and if for a real number, then is called a lower indefinite cut set in the domain of f at the level.

We now give the following main result:

Theorem 2.1. Let g and f be real-valued functions on a topological space x with. If there exists a strong binary relation ρ on the power set of x and if there exist lower indefinite cut sets and in the domain of f and g at the level t for each rational number t such that if then, then there exists a continuous function h defined on X such that.

Proof. Let g and f be real-valued functions defined on x such that. By hypothesis there exists a strong binary relation ρ on the power set of x and there exist lower indefinite cut sets and in the domain of f and g at the level t for each rational number t such that if then.

Define functions F and g mapping the rational numbers into the power set of X by and. If and are any elements of with, then, and. By Lemmas 1 and 2 of [7] it follows that there exists a function h mapping into the power set of X such that if and are any rational numbers with, then and.

For any x in x, let.

We first verify that: If x is in then x is in for any; since x is in implies that, it follows that. Hence. If x is not in, then x is not in for any; since x is not in implies that, it follows that. Hence.

Also, for any rational numbers and with, we have. Hence is an open subset of X, i.e., h is a continuous function on x.

The above proof used the technique of proof of Theorem 1 of [6] .

3. Applications

The abbreviations and are used for α-continuous and c-continuous, respectively.

Corollary 3.1. If for each pair of disjoint α-closed (resp. c-closed) sets of X , there exist open sets and of X such that, and then X has the weak c-insertion property for (resp.).

Proof. Let g and f be real-valued functions defined on the X, such that f and g are (resp.), and. If a binary relation ρ is defined by in case (resp.), then by hypothesis ρ is a strong binary relation in the power set of x. If and are any elements of with, then

since is an α-closed (resp. c-closed) set and since is an α-open (resp. c-open) set, it follows that (resp.). Hence implies that. The proof follows from Theorem 2.1.

Corollary 3.2. If for each pair of disjoint α-closed (resp. c-closed) sets, there exist open sets and such that, and then every α-continuous (resp. c-continuous) function is continuous.

Proof. Let f be a real-valued α-continuous (resp. c-continuous) function defined on the X. Set, then by Corollary 3.1, there exists a continuous function h such that.

Corollary 3.3. If for each pair of disjoint subsets of X , such that is α-closed and is C-closed, there exist open subsets and of X such that, and then x have the weak c-insertion property for and.

Proof. Let g and f be real-valued functions defined on the X, such that g is ac (resp.) and f is (resp. ac), with. If a binary relation ρ is defined by in case (resp.), then by hypothesis ρ is a strong binary relation in the power set of X. If and are any elements of with, then

since is a c-closed (resp. α-closed) set and since is an α-open (resp. c-open) set, it follows that (resp.). Hence implies that. The proof follows from Theorem 2.1.

Acknowledgements

This research was partially supported by Centre of Excellence for Mathematics(University of Isfahan).

NOTES

^*This work was supported by University of Isfahan and Centre of Excellence for Mathematics (University of Isfahan).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Hatir, E., Noiri, T. and Yksel, S. (1996) A Decomposition of Continuity. Acta Mathematica Hungarica, 70, 145-150. http://dx.doi.org/10.1007/BF00113919
[2]	Dontchev, J. (1998) Between α- and β-Sets. Mathematica Balkanica, 12, 295-302.
[3]	Przemski, M. (1993) A Decomposition of Continuity and α-Continuity. Acta Mathematica Hungarica, 61, 93-98. http://dx.doi.org/10.1007/BF01872101
[4]	Dontchev, J. (1995) The Characterization of Some Peculiar Topological Space via α- and β-Sets. Acta Mathematica Hungarica, 69, 67-71. http://dx.doi.org/10.1007/BF01874608
[5]	Ganster, M. and Reilly, I. (1990) A Decomposition of Continuity. Acta Mathematica Hungarica, 56, 299-301. http://dx.doi.org/10.1007/BF01903846
[6]	Katětov, M. (1951) On Real-Valued Functions in Topological Spaces. Fundamenta Mathematicae, 38, 85-91.
[7]	Katětov, M. (1953) Correction to, “On Real-Valued Functions in Topological Spaces”. Fundamenta Mathematicae, 40, 203-205.
[8]	Brooks, F. (1971) Indefinite Cut Sets for Real Functions. The American Mathematical Monthly, 78, 1007-1010. http://dx.doi.org/10.2307/2317815
[9]	Lane, E. (1976) Insertion of a Continuous Function. Pacific Journal of Mathematics, 66, 181-190. http://dx.doi.org/10.2140/pjm.1976.66.181