Constructing a Subsequence of (Exp(in))_n∈N Converging towards Exp(iα) for a Given α∈R

Vito Lampret

University of Ljubljana, Ljubljana, Slovenia.

DOI: 10.4236/oalib.1102135                

Abstract

For a given positive irrational and a real t ∈ [0,1), the explicit construction of a sequence of positive integers, such that the sequence of fractional parts of products converges towards t, is given. Moreover, a constructive and quantitative demonstration of the well known fact, that the ranges of the functions cos and sin are dense in the interval [-1,1], is presented. More precisely, for any α ∈ R, a sequence of positive integers is constructed explicitly in such a way that the estimate holds true for any j ∈ N. The technique used in the paper can give more general results, e.g. by replacing sine or cosine with continuous function f: R→R having an irrational period.

Keywords

Convergence, Dense, Estimate, Exponential, Fractional Part, Integer Part, Irrational, Limit Point, Sequence

holds true for any. The technique used in the paper can give more general results, e.g. by replacing sine or cosine with continuous function 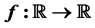having an irrational period.

Keywords:

Subject Areas: Mathematical Analysis, Number Theory, Numerical Mathematics

1. Introduction

There are several arguments known showing that the ranges of the sequences 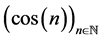and to be dense in the interval (see for example [1] , Problem 4.22, p. 33 and [2] , Problem 1.4.26, p. 45). In [3] the authors considered the limit points of the sequence rather constructively. Subsequently Ogilvy [4] presented more elegant but less direct analysis. In [5] it was demonstrated, on the basis of continued fraction

theory, that the set is dense too in. Recently, these results were generalized in some

directions in [6] , considering instead of cosine and sine, a continuous function having an irrational

period. As a corollary the authors obtained that the sets and are dense in

. However, it was not confirmed in [6] that is dense too in. The technique used in the above cited literature is more or less constructive or quantitative. To the best knowledge of the author, the most constructive approach to the problem of denseness of the sequence or more general of the sequence for a continuous function having an irrational period can be found in [7] .

We offer a concrete―direct, constructive and also quantitative (computational) approach to the limit points of

the sequences and, i.e. to the limit points of complex-valued sequence.

The idea of continued fraction representation of a number suggests how to construct an algorithm producing a sequence of positive integers such that by applying the functions sin and cos we obtain two convergent sequences with prescribed limits in the interval. Crucial is the well-known fact that for any irrational number the fractional parts, , are dense in. The purpose of the paper is to construct explicitly, for any positive irrational and any, the sequence of positive integers such that the sequence of fractional parts of products converges towards t, and consequently, to construct explicitly, for any, the sequence of positive integers such that the estimate

holds true for any.

2. Preliminaries

We begin with formal definition making possible to construct the desired sequence.

¹The literature usually uses for fractional part of x different notations such as for example or or even. The last one symbol is not suitable due to possible confusion with the singleton containing the only element x.

Definition 2.1 For any the integer part or floor and the fractional part of x are defined as follows¹:

As an immediate consequence of this definition we have, for any:

1) (1)

2) (2)

Moreover, for any positive irrational number and any positive integer n there exist (only one) non-nega- tive number k and (only one) such that

(3)

Indeed, considering Definition above, the numbers and confirm the assertion. Namely, using (1), we have and, i.e. with irrational.

The crucial role is played by the following lemma.

Lemma 2.2. Let, , and let be such that. Then

there exist and such that, , and. Construc- tively, letting

the numbers

verify the statement.

Proof. Let us suppose that

(4)

Then. Hence, the integer and, considering (1), , i.e.

(5)

Moreover,

(6)

where and

(7)

Consequently,

(8)

Now, we distinguish two cases: (A) and (B).

(A) In this case we can set in Lemma 2.2 the integers and, and the fractional part.

(B) In this case we have the difference

(9)

Therefore, there exists an integer such that the inequality

(10)

holds. Now, referring to (4), (6) and (8), we have

Hence,

(11)

where

(12)

and, according to (8),

(13)

Since, due to (10) and (13), we can take in Lemma 2.2 the integers, and.

We also note that the integer satisfies the estimate

i.e., referring to (9), we have

Thus, satisfies (10) and for every p satisfying (10). Moreover, in case (B), we have. But, this estimate implies the inequality. Consequently, , i.e. we have. Hence,

in case (B), we estimate and.

Corollary 2.3. Let be any positive irrational, any positive integer and for every let us define

1)

2)

3)

4)

5)

6)

In this way we obtain the sequences and of positive integers and the sequence such that for any there hold the following relations:

i)

ii) and

iii).

iv).

Proof. For the sequences, which are given inductively, we can apply the preceding Lemma 2.2 to verify the assertions i)-iii) of the Corollary 2.3. Concerning the estimate iv), it is certainly true for and, if for some, then, using iii), we have

.

Remark 2.4. The estimate iii) in Corollary 2.3 is rather sharp as is illustrated² in Figure 1 where the graph of the sequence is depicted using.

Remark 2.5. The estimate iv) in Corollary 2.3 seems to be rather rough as it is evident from Figure 2 showing the graph of the sequence.

Remark 2.6. Given positive irrational, smaller is the factor in Corollary 2.3 iv) faster is the convergence as. Therefore, for the initial number in Corollary 2.3 a positive

integer m should be chosen in such a way that the number should be as small as possi-

ble. The Table 1 illustrates the dynamics of the sequence.

Remark 2.7. The Table 2 shows, for, the dynamics of the sequences and. The latter grows very fast. However, if we put, for example, in Corollary 2.3, we would get a sequence that would grow a bit more slowly. By experimenting with Mathematica [8] we come to the conjecture that

for and. However, this is only a hypothesis.

3. Denseness

Theorem 3.1. For being any positive irrational, and, using the sequences and from Corollary 2.3, let us define

1),

2).

Figure 1. The graph of the sequence.

Figure 2. The graph of the sequence.

Table 1. Dynamics of the sequence.

Table 2. Dynamics of the sequences and.

Then the sequence converges towards t as. Hence, the sequence of fractional parts of products, , is dense in the interval.

For several, Figure 3 and Figure 4 on page 7 illustrate convergence of the sequence towards t, using.

Proof. Let us take and. Now, considering Corollary 2.3 iv), we estimate

Therefore, according to the definition i) of and considering the equivalence (1) on page 2, we have and

Consequently, again thanks to Corollary 2.3 iv),

or

(14)

Now, for, using the definition ii) of and considering Corollary 2.3 i), we have

or

(15)

Also, using (14),

holds for

Thus, according to (15), the fractional part of is equal to, for, and, thanks to (14), converges towards t as.

Theorem 3.2. The closures of the sets and are equal to the interval. More constructively, setting in Corollary 2.3, and considering the sequences and defined in Corollary 2.3, let us define, for any and,

1)

2).

Then

(16)

The estimate (16) is illustrated on the Figure 5 where is plotted the graph of the sequence together with the graph of continuous function.

Proof. Assume that all the suppositions of Theorem 3.2 are fulfilled. Then, since

we have, considering Corollary 2.3 iv), the estimate, i.e.

(17)

Moreover, referring to the definition of,

Figure 3. The graphs of the sequences using.

Figure 4. The graphs of the sequences using.

Figure 5. The graph of the sequence and the graph of continuous function.

That is, considering (17), we estimate

(18)

Now, according to Corollary 2.3, we have

Hence,

(19)

To conclude the proof we estimate

(20)

for. For such h we also have

(21)

The relations (18)-(21) imply the inequalities

verifying (16).

4. Conclusions

Using only elementary tools, no use of convergents of continued fraction theory, we derived two main results about the denseness:

1) For any positive irrational and every we constructed inductively a sequence of positive integers such that the appropriate sequence of fractional parts of products converges towards t.

2) We demonstrated constructively and quantitatively the well known fact that the ranges of cosine and sine are dense in the interval; for any real we constructed inductively the sequence of positive integers such that, for any.

In [7] is presented very nice approach to the denseness problem which is also constructive. Essential for this paper are two lemmas.

Lemma A. [Lemma 1, p. 402] Let L be any irrational number greater than 1, and suppose that, and for. Then the sequence is well defined and

for all.

Lemma B. [Lemma 2, p. 403] For each x_k defined in Lemma A we can find integers m_k and n_k such that, with and for. As the consequence of these lemmas in [7] is constructively proved the next theorem.

Theorem. [Theorem 3, p. 404] Let be continuous function with irrational period. Then, for any

point in the range of f, there exists a sequence of positive integers such that.

This theorem could be proved and expanded also using our technique.

NOTES

²In this article all figures are produced using Mathematica [8] .

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Aliprantis, C.D. and Burkinshaw, O. (1999) Problems in Real Analysis—A Workbook with Solutions. Academic Press, Inc., San Diego.
[2]	Rădulescu, T.-L.T., Rădulescu, V.D. and Andreescu, T. (2009) Problems in Real Analysis—Advanced Calculus on the Real Axis. Springer, Dodrecht, Heidelberg, New York. http://dx.doi.org/10.1007/978-0-387-77379-7
[3]	Staib, J.H. and Demos, M.S. (1967) On the Limit Points of the Sequence {sin n }. Mathematics Magazine, 40, 210-213. http://dx.doi.org/10.2307/2688681
[4]	Ogilvy, S.C. (1969) The Sequence {sin n } . Mathematics Magazine, 42, 94.
[5]	Luca, F. (1999) {(cos(n))n} n≥1 is dense in[-1,1] . Bulletin Mathématique de la Société des Sciences Mathématiques de Roumanie—Nouvelle Série, 42, 369-376.
[6]	Ahmadi, M.F. and Hedayatian, K. (2006) Limit Points of Trigonometric Sequences. Journal of Mathematical Extension, 1, 21-26.
[7]	Zheng, S. and Cheng, J.C. (1999) Density of the Images of Integers under Continuous Functions with Irrational Periods. Mathematics Magazine, 72, 402-404. http://dx.doi.org/10.2307/2690800
[8]	Wolfram, S. (1988-2008) Mathematica—Version 8.0. Wolfram Research, Inc., Champaign, IL.