Received 9 September 2015; accepted 3 April 2016; published 6 April 2016

1. Introduction
Let G be a graph with vertex set V and edge set E. A subset I of V is independent if no two vertices in I are adjacent. A subset S of V is a dominating set if every vertex in 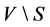 is adjacent to at least one vertex in S. We define a coloring C of G with k colors to be a partition of V into k independent sets:
is adjacent to at least one vertex in S. We define a coloring C of G with k colors to be a partition of V into k independent sets:
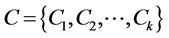
such that

and  is independent for
is independent for . The minimum of k for which such a partition is possible is the chromatic number of G, denoted
. The minimum of k for which such a partition is possible is the chromatic number of G, denoted . The dominating-c-color number of G is motivated by a two-stage optimization problem. First, we partition the vertex set of G into the minimum number of independent sets; secondly, we maximize the independent sets that are also dominating in G. Clearly, the number of independent sets we use in the first stage will be
. The dominating-c-color number of G is motivated by a two-stage optimization problem. First, we partition the vertex set of G into the minimum number of independent sets; secondly, we maximize the independent sets that are also dominating in G. Clearly, the number of independent sets we use in the first stage will be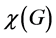 , the chromatic number of G. Among all colorings of G using
, the chromatic number of G. Among all colorings of G using 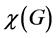 colors, the maximum number of independent sets that are also dominating is defined to be the dominating- c-color number of G, denoted by
colors, the maximum number of independent sets that are also dominating is defined to be the dominating- c-color number of G, denoted by![]() . Formally, we have
. Formally, we have
![]()
The dominating-c-color number of G was first introduced in [2] . More research has been done in this area since then (see for example [1] [3] [4] ). However, the two interesting questions posed in [1] and [2] remain unanswered. In this article, we present some more results about the dominating-c-color number of a graph that are relevant to these two questions.
2. Main Results
The following observation was made in [2] .
Theorem 1 For all graph G, ![]()
The following two questions are posed in [1] and [2] .
Question 1. Characterize the graphs G for which ![]()
Question 2. Characterize the graphs G for which ![]()
Neither of the two extreme cases is trivial. It is known that if G has an isolated vertex, then![]() . However, a graph G with
. However, a graph G with ![]() can be connected and have arbitrarily large minimum degree.
can be connected and have arbitrarily large minimum degree.
Theorem 2. [1] For every integer ![]() there exists a connected graph G with
there exists a connected graph G with ![]() and
and ![]()
The following lemma may help us understand the relation between the structure of a graph and its dominating-c-color number. It shows that if a graph G contains a complete bipartite graph as a spanning subgraph, then the dominating-c-color number of G is the sum of the dominating-c-color numbers of these two subgraphs.
Lemma 1. If ![]() can be partitioned into two sets
can be partitioned into two sets ![]() and
and ![]() such that every vertex in
such that every vertex in ![]() is adjacent to every vertex in
is adjacent to every vertex in![]() , then
, then ![]() where
where ![]() is the subgraph of G induced by
is the subgraph of G induced by ![]() for
for![]() .
.
Proof. Since in any coloring of G, no vertex in ![]() can share a color with a vertex in
can share a color with a vertex in![]() , we have
, we have![]() . Let
. Let ![]() and
and![]() . Let
. Let ![]() be a
be a ![]() -coloring of
-coloring of ![]() with
with ![]() dominating coloring classes using the colors
dominating coloring classes using the colors![]() . Let
. Let ![]() be a
be a ![]() -coloring of
-coloring of ![]() with
with ![]() dominating coloring classes using the colors
dominating coloring classes using the colors![]() . The combination of
. The combination of ![]() and
and ![]() is clearly a
is clearly a ![]() -coloring of G. A coloring class of C is either a coloring class of
-coloring of G. A coloring class of C is either a coloring class of ![]() or a coloring class of
or a coloring class of![]() . Suppose that S is a coloring class of
. Suppose that S is a coloring class of ![]() that dominates
that dominates![]() . Every vertex in
. Every vertex in ![]() is adjacent to at least one vertex in S. Every vertex in
is adjacent to at least one vertex in S. Every vertex in ![]() is adjacent to every vertex in
is adjacent to every vertex in![]() . Therefore S is a dominating set in G. Similarly, every coloring class of
. Therefore S is a dominating set in G. Similarly, every coloring class of ![]() that dominates
that dominates ![]() is a dominating set in G. C is a coloring of G with at least
is a dominating set in G. C is a coloring of G with at least ![]() coloring classes. We have
coloring classes. We have ![]()
Suppose that ![]() is a coloring of G with
is a coloring of G with ![]() colors and
colors and ![]() dominating coloring classes. The restriction of
dominating coloring classes. The restriction of ![]() to
to ![]() is a coloring of
is a coloring of ![]() with
with ![]() colors for
colors for![]() . Let S be a dominating coloring class of
. Let S be a dominating coloring class of![]() .
. ![]() or
or![]() . Suppose that
. Suppose that![]() . Then S is a dominating set for
. Then S is a dominating set for![]() . Therefore, every dominating coloring class of
. Therefore, every dominating coloring class of ![]() is either a dominating coloring class of
is either a dominating coloring class of ![]() or a dominating coloring class of
or a dominating coloring class of![]() . Therefore
. Therefore ![]()
Using Lemma 1, we have a sufficient condition for the dominating-c-color number of a graph to be greater than one.
Corollary 1. If the complement of G is disconnected, then![]() .
.
The join of two graphs ![]() and
and![]() , denoted by
, denoted by![]() , is defined by
, is defined by
![]()
![]()
In other words, we construct ![]() by taking a copy of each of
by taking a copy of each of ![]() and
and ![]() and joining every vertex in
and joining every vertex in ![]() with every vertex in
with every vertex in![]() . It is known that
. It is known that ![]() By Lemma 1, there is a similar relation between the dominating-c-color numbers.
By Lemma 1, there is a similar relation between the dominating-c-color numbers.
Theorem 3. ![]()
It is shown in [1] that it is possible for a graph with chromatic number k to have dominating-c-color number l for any k such that ![]() and
and![]() . We present a new construction to prove this result using Theorem 3.
. We present a new construction to prove this result using Theorem 3.
Theorem 4. For all integers ![]() such that
such that ![]() and
and ![]() there exists a connected graph G with
there exists a connected graph G with ![]() and
and![]() .
.
Proof. We prove by induction on l. If![]() , the existence of such graphs is guaranteed by Theorem 2. For
, the existence of such graphs is guaranteed by Theorem 2. For ![]() it is easy to check that
it is easy to check that ![]() and
and ![]() Therefore the theorem is true for
Therefore the theorem is true for![]() . Suppose that
. Suppose that ![]() and
and ![]() Let
Let ![]() and
and ![]()
![]() By inductive hypothesis, there is a connected graph H with
By inductive hypothesis, there is a connected graph H with ![]() and
and![]() . Let
. Let ![]() Since
Since![]() , by Theorem 3 we have
, by Theorem 3 we have
![]()
and
![]()
This proves the theorem.
Next we turn our attention to Question 2. Arumugam et al. [2] showed that if G is uniquely c-colorable, then![]() . Therefore if G contains a subgraph that is uniquely
. Therefore if G contains a subgraph that is uniquely ![]() -colorable, then
-colorable, then![]() . It is natural to ask whether there are any other kind of such graph, that is, whether there are any graph G such that
. It is natural to ask whether there are any other kind of such graph, that is, whether there are any graph G such that ![]() and G does not contain a uniquely k-colorable subgraph. For
and G does not contain a uniquely k-colorable subgraph. For![]() , the answer is no since every edge is a uniquely 2-colorable subgraph. For
, the answer is no since every edge is a uniquely 2-colorable subgraph. For![]() , the answer is yes. Arumugam et al. [1] showed that
, the answer is yes. Arumugam et al. [1] showed that ![]() for any nonnegative integer i.
for any nonnegative integer i. ![]() was not uniquely 3-colorable for
was not uniquely 3-colorable for![]() . Using this fact and Theorem 3, we can show that the answer of our question is yes for all
. Using this fact and Theorem 3, we can show that the answer of our question is yes for all![]() .
.
First, we need a technical lemma.
Lemma 2. The graph ![]() is uniquely
is uniquely ![]() -colorable if and only if
-colorable if and only if ![]() is uniquely
is uniquely ![]() -colorable and
-colorable and ![]() is uniquely
is uniquely ![]() -colorable.
-colorable.
The proof is easy and omitted.
Theorem 5. Let k be an integer greater than 3. There is a graph ![]() such that
such that ![]() and
and ![]() do not contain a uniquely k-colorable subgraph.
do not contain a uniquely k-colorable subgraph.
Proof. We prove by induction on k. We have shown that the statement is true for![]() . Suppose that
. Suppose that ![]() and the statement is true for
and the statement is true for![]() . Let
. Let ![]() Since
Since ![]()
![]() by Theorem 3 and the inductive hypothesis. Every k-chromatic subgraph H of
by Theorem 3 and the inductive hypothesis. Every k-chromatic subgraph H of ![]() must have the form
must have the form ![]() where
where ![]() is a subgraph of
is a subgraph of![]() . By Lemma 2, H is uniquely k-colorable if and only if
. By Lemma 2, H is uniquely k-colorable if and only if ![]() is uniquely
is uniquely ![]() -colorable. Since
-colorable. Since ![]() does not contain a uniquely
does not contain a uniquely ![]() - colorable subgraph,
- colorable subgraph, ![]() does not contain any uniquely k-colorable subgraph. This proves the theorem.
does not contain any uniquely k-colorable subgraph. This proves the theorem.
The graphs constructed in Theorem 5 contain large cliques. In fact, ![]() contains many copies of
contains many copies of![]() . If
. If ![]() for some integers l and j, we may reduce the size of the largest clique in
for some integers l and j, we may reduce the size of the largest clique in ![]() by taking the join of copies of
by taking the join of copies of ![]() in the first l steps and then taking the join with
in the first l steps and then taking the join with ![]() afterwards. Thus, we have the following result.
afterwards. Thus, we have the following result.
Theorem 6. Let ![]() be nonnegative integers and
be nonnegative integers and![]() . There is a graph
. There is a graph ![]() such that
such that![]() .
. ![]() does not contain a uniquely k-colorable subgraph and the largest clique in
does not contain a uniquely k-colorable subgraph and the largest clique in ![]() has size
has size![]() .
.
3. Remarks
It is well known that there are uniquely k-colorable graphs with arbitrarily large girth. Therefore, there are graphs G such that ![]() and G has arbitrarily large girth. In light of Theorems 5 and 6, we would like to ask the following question.
and G has arbitrarily large girth. In light of Theorems 5 and 6, we would like to ask the following question.
Question 3. Are there triangle-free graphs G such that ![]() and does G not contain a uniquely k-colorable graph? Furthermore, are there such graphs with arbitrarily large girth?
and does G not contain a uniquely k-colorable graph? Furthermore, are there such graphs with arbitrarily large girth?