Exact Traveling Wave Solutions for the (1 + 1)-Dimensional Compound KdVB Equation via the Novel (G'/G)-Expansion Method

Md. Nur Alam^1*, Fethi Bin Muhammad Belgacem²

¹Department of Mathematics, Pabna University of Science & Technology, Pabna, Bangladesh.
²Department of Mathematics, Faculty of Basic Education, PAAET, Al-Ardhiya, Kuwait.

DOI: 10.4236/ijmnta.2016.51003                

Abstract

In this work, while applying a new and novel (G'/G)-expansion version technique, we identify four families of the traveling wave solutions to the (1 + 1)-dimensional compound KdVB equation. The exact solutions are derived, in terms of hyperbolic, trigonometric and rational functions, involving various parameters. When the parameters are tuned to special values, both solitary, and periodic wave models are distinguished. State of the art symbolic algebra graphical representations and dynamical interpretations of the obtained solutions physics are provided and discussed. This in turn ends up revealing salient solutions features and demonstrating the used method efficiency.

Keywords

Novel (G'/G)-Expansion Method, The (1 + 1)-Dimensional Compound KdVB Equation, Traveling Wave Solutions, Solitary Wave Solutions, Solitons

Received 10 January 2016; accepted 29 February 2016; published 3 March 2016

1. Introduction

Nonlinear Evolution Equations (NLEEs) are encountered in various fields of engineering, and many theoretical and applied sciences physics, such as applied mathematics, chemistry, biology and many applications. Exact analytical solutions of NLEEs have come to play a significant role in understanding of qualitative nature of many phenomena, and the suitable modeling of corresponding processes, in different areas of applied science. Graphical representations of solutions of the NLEEs equations permit the unscrambling of mechanisms pertaining to compound nonlinear phenomena. This includes for instance spatial localization of transfer processes, multiplicity or non-appearance steady states under different conditions, and existence of peaking regimes. Even special exact solutions data that may seem not to have a clear physical meaning, can often be used as test problems to verify processes reliability, and help estimate errors of various numerical, asymptotic, and approximate analytical methods.

Exact solutions can also serve as a basis for perfecting and testing computer algebra software packages, designed for solving NLEEs. Furthermore, exact solutions allow researchers to design and run experiments, by creating appropriate natural conditions, to determine these parameters or functions. Therefore, investigations of exact traveling wave solutions are becoming increasingly attractive in nonlinear phenomena investigations and analyses. On the other hand, not all equations posed by the advent of NLEEs models are readily solvable. As a result, many original techniques have been successfully urbanized by various groups of researchers, such as the Cole-Hopf transformation method [1] , the Miura transformation method [2] , the Hirota’s bilinear method [3] , the 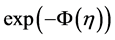-expansion method [4] - [6] , the Sumudu transform method [7] - [14] , the Fan sub-equation method [15] [16] , the spectral-homotopy analysis method [17] [18] , the least-squares finite element scheme [19] , the (G′/G)-expansion method [20] - [23] , the improved (G′/G)-expansion method [24] , the trial function method [25] , the nonlinear transform method [26] , the extended Tanh-function method [27] [28] , and the novel (G′/G)- expansion method [29] - [34] , homotopy analysis method [35] , to name a few. The latter sequence of papers really constituted a ladder honed in the current wealth of repeated experimental and theoretical successes that sprang us to the work at hand, that we hope will greatly benefit the readership, towards the further understanding of NLEEs dynamics and solutions, and mechanisms for recognizing and classifying them.

The aim of this article is to demonstrate the efficiency of the novel (G′/G)-expansion method to exhibit exact solutions for NLEEs in mathematical physics via the (1 + 1)-dimensional compound KdVB equation [36] . This equation can be thought of as a generalization of KdV-mKdV and Burgers equations, involving nonlinear dispersion and dissipation effects (see for instance [37] ). Below, twenty-five solutions, stratified into four separate families are stratified for the (1 + 1)-dimensional compound KdVB equation.

2. The Novel (G′/G)-Expansion Method

Suppose the nonlinear evolution equation,

(1)

where, 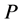, is a polynomial in the function, , and its partial derivatives. The main steps of the novel (G′/G)-expansion method are:

Step 1: Combining the real variables 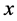and 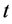by a complex variable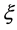, we suppose that

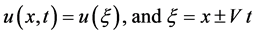(2)

where 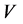is the speed of the traveling wave. Equation (2) is then used to transforms Equation (1) into an ODE for:

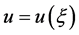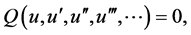(3)

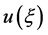where is a function of and its derivatives wherein prime stands for derivative with respect to.

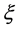Step 2: Assuming that the solution of Equation (3) can be expressed in terms of powers in,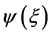

(4)

where,

(5)

with,.

Herein or may be zero, but not simultaneously, the, and are constants to be determined later. The function, satisfies the second order nonlinear ODE:

(6)

where prime denotes differentiation with respect.

Using the Hopf-Cole transformation, , reduces the Equation (6) into Riccati

equation,

(7)

We like to recall that Equation (7) can exhibit a plethora of solutions in the number of twenty five as in (Zhu [39] ).

Step 3: The value of the positive integer can be determined by balancing the highest order linear terms with the nonlinear terms of the highest order come out in Equation (3). If the degree of is, then the degree of the other expressions will be as follows:

Step 4: Substitute Equation (4) including Equations. (5) and (6) into Equation (3), we obtain polynomials in

and,. Next we collect each coefficient of the resulted

polynomials to zero, yields an over-determined set of algebraic equations for, and.

Step 5: Suppose that the value of the constants can be obtained by solving the algebraic equations obtained in Step 4, then substituting the values of the constants together with the solutions of Equation (6), will yield new and comprehensive exact traveling wave solutions of the nonlinear evolution equation (1).

3. Application of the Novel (G′/G)-Expansion Method

Let us consider the (1 + 1)-dimensional compound KdVB equation,

(8)

Using the traveling wave transformation, Equation (8) is converted into the following ODE:

(9)

Integrating Equation (9), we obtain

(10)

where is a constant of integration. Inserting Equation (4) into Equation (10) and balancing the highest order derivative with the nonlinear term of the highest order, we obtain.

Therefore, the solution of Equation (10) takes the form,

(11)

Substituting Equation (11) into Equation (10), the left hand side is transformed into polynomials of

and,. Equating the coefficients of like power of these

polynomials to zero, we obtain an over-determine set of algebraic equations (for simplicity we leave out to display the equations) for, , , , and. Solving the over-determined set of algebraic equations by using the symbolic computation software, such as Maple 13, we obtain

(12)

Substituting Equation (12) into Equation (11), with, , , , , and, being arbitrary constants. We obtain

(13)

Substituting the solutions of the Equation (6) into Equation (13) and simplifying, we obtain the following solutions:

When and (or),

(14)

where, and, , , , and are arbitrary constants.

With A & B real constants, when occurring in expressions, the next solutions, are given by,

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

When and (or),

(25)

(26)

(27)

(28)

(29)

(30)

(31)

where and are arbitrary constants such that.

(32)

(33)

(34)

(35)

When and, where k is an arbitrary constant.

(36)

(37)

where is an arbitrary constant.

When and, the solution of Equation (8) is,

(38)

where is an arbitrary constant.

4. Discussions and Conclusions

Here, we first discuss physical interpretation, and graphical representation of four families of solutions determined above. The introduction of dispersion without introducing nonlinearity destroys the solitary wave as different Fourier harmonics start propagating at different group velocities. On the other hand, introducing nonlinearity without dispersion also prevents the formation of solitary waves, because the pulse energy is frequently pumped into higher frequency modes. However, if both dispersion and nonlinearity are present, solitary waves can be sustained. Similarly to dispersion, dissipation can also give rise to solitary waves when combined with nonlinearity. Hence, it is interesting to point out the delicate balance between the nonlinearity effect of and, and the dissipative effect of. The gives rise to solitons that after a fully interaction with others the solitons come back retaining their identities with the same speed and shape.

The (1 + 1)-dimensional compound KdVB equation has solitary wave solutions that have exponentially decaying wings. If two solitons of the (1 + 1)-dimensional compound KdVB equation collide, the solitons just pass through each other and emerge unchanged. For special values of the parameters solitary wave solutions are originated from the obtained exact solutions.

Figure 1: Kink solution, shape of Equation (14) when and Solution of Equations (14), (16), (19), (22), (23), (36) and (37) represents kink. Kink waves are traveling waves which arise from one asymptotic state to another. The kink solutions are approach to a constant at infinity. Other figures are omitted for convenience.

Figure 2: Single soliton, shape of Equation (15) when and Solution of Equations (15), (17), (18), (26), (28) and (29) represents single soliton. Solitons are special kinds of solitary waves. The soliton solution is a specially localized solution, hence as,. Solitons have a remarkable property that it keeps its identity upon interacting with other solitons. Other figures are omitted for convenience.

Figure 3: Modulus plot of periodic wave solutions, shape of Equation (25) when , and Solution of Equations (25), (27), (30)-(35) represents periodic wave solutions. Periodic solutions are traveling wave solutions that are periodic such as. Other figures are omitted for convenience.

Figure 4: Singular kink solution, shape of Equation (38) when , and Solution of Equations (20), (21), (24) and (38) represents singular kink solutions. Other figures are omitted for convenience.

The graphical illustrations of the solutions are depicted in the Figures 1-4 with the aid of commercial software Maple.

Comparison between Zayed [38] solutions and our solutions: Zayed [38] considered solutions of the (1 + 1)- dimensional compound KdVB equation using the basic -expansion method combined with the Riccati equation. The solutions of the (1 + 1)-dimensional compound KdVB equation obtained by the novel - expansion method are different from those of the basic -expansion method combined with the Riccati equation. Moreover, Zayed [38] investigated the well-established (1 + 1)-dimensional compound KdVB equation to obtain exact solutions via the basic -expansion method and achieved only five solutions (see Appendix). Furthermore, twenty-five solutions of the well-known (1 + 1)-dimensional compound KdVB equation are constructed by applying the novel -expansion method. On the other hand, the auxiliary equation used in this paper is different, so obtained solutions are also different. Similarly for any nonlinear evolution equation it can be shown that the novel -expansion method is much easier than other methods.

Figure 1. Kink solution, shape of Equation (14) when , and

Figure 2. Single soliton, shape of Equation (15) when , and

Figure 3. Modulus plot of periodic wave solutions, shape of Equation (25) when , and

Figure 4. Singular kink solution, shape of Equation (38) when , and

In this paper, the novel -expansion method has been successfully applied to find the traveling wave solutions for the (1 + 1)-dimensional compound KdVB equation. The method has been used to find new exact solutions. As a result, hyperbolic function solutions, rational function solutions and trigonometric function solutions with several free parameters have been obtained. The solutions gotten with tuned parameters may be used to detect and explain complex physical phenomena. Results in this paper show that the devised algorithm is highly effective, and can be used for many other NLEEs in mathematical physics. Thus, we can say that the novel (G/G)-expansion method can be extended to solve the problems of nonlinear evolution equations arising in the theory of solitons, and other nonlinear sciences. Consequently, thus far not only were we successful at solving the KdVB equation, but also, we contributed to establishing the novel -expansion method as a versatile and efficient tool that can be applied to NLEEs.

Acknowledgements

Fethi Bin Muhammad Belgacem is pleased to acknowledge the continued support of the Public Authority for Applied Education and Training Research Department, (PAAET RD), in Kuwait through grant BE-13-09.

Appendix. Zayed Solutions [38]

Zayed [38] examined the exact solutions of the nonlinear (1 + 1)-dimensional compound KdVB equation by using the -expansion method. They found the following five solutions of the form,

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	[1] Salas, A.H. and Gomez, C.A. (2010) Application of the Cole-Hopf Transformation for Finding Exact Solutions to Several Forms of the Seventh-Order KdV Equation. Mathematical Problems in Engineering, 2010, Article ID: 194329. http://dx.doi.org/10.1155/2010/194329
[2]	Bock, T.L. and Kruskal, M.D. (1979) A Two-Parameter Miura Transformation of the Benjamin-One Equation. Physics Letters A, 74, 173-176. http://dx.doi.org/10.1016/0375-9601(79)90762-X
[3]	Wazwaz, A.M. (2012) Multiple-Soliton Solutions for a (3 + 1)-Dimensional Generalized KP Equation. Communications in Nonlinear Science and Numerical Simulation, 17, 491-495. http://dx.doi.org/10.1016/j.cnsns.2011.05.025
[4]	Hafez, M.G. and Alam, M.N. (2015) Exact Solutions for Some Important Nonlinear Physical Models via (2 + 1)-Dimensional Sine-Gordon Equation, (2 + 1)-Dimensional Sinh-Gordon Equation, DBM Equation and TBM Equations. Asian Journal of Mathematics and Computer Research, 5, 157-174.
[5]	Alam, M.N., Hafez, M.G., Akbar, M.A. and Roshid, H.O. (2015) Exact Solutions to the (2 + 1)-Dimensional Boussinesq Equation via exp(Φ(η))-Expansion Method. Journal of Scientometric Research, 7, 1-10. http://dx.doi.org/10.3329/jsr.v7i3.17954
[6]	Hatez, M.G., Alam, M.N. and Akbar, M.A. (2014) Application of the -Expansion Method to Find Exact Solutions for the Solitary Wave Equation in an Unmagnatized Dusty Plasma. World Applied Sciences Journal, 32, 2150-2155.
[7]	Belgacem, F.B.M., Karaballi, A.A. and Kalla, S.L. (2003) Analytical Investigations of the Sumudu Transform and Applications to Integral Production Equations. Mathematical Problems in Engineering, 2003, 103-118. http://dx.doi.org/10.1155/S1024123X03207018
[8]	Belgacem, F.B.M. (2006) Introducing and Analyzing Deeper Sumudu Properties. Nonlinear Studies, 13, 23-41.
[9]	Belgacem, F.B.M. (2010) Sumudu Transform Applications to Bessel Functions and Equations. Applied Mathematical Sciences, 4, 3665-3686.
[10]	Belgacem, F.B.M. and Karaballi, A.A. (2006) Sumudu Transform Fundamental Properties Investigations and Applications. Journal of Applied Mathematics and Stochastic Analysis, 2006, Article ID: 91083. http://dx.doi.org/10.1155/JAMSA/2006/91083
[11]	Bulut, H., Baskonus, H.M. and Tuluce, S. (2012) Homotopy Perturbation Sumudu Transform Method for One-Two-Three Dimensional Initial Value Problems. e-Journal of New World Sciences Academy, 7, 55-65.
[12]	Bulut, H., Baskonus, H.M. and Tuluce, S. (2012) The Solution of Wave Equations by Sumudu Transform Method. Journal of Advanced Research in Applied Mathematics, 4, 66-72. http://dx.doi.org/10.5373/jaram.1317.021812
[13]	Bulut, H., Baskonus, H.M. and Tuluce, S. (2012) The Solutions of Partial Differential Equations with Variable Coefficient by Sumudu Transform Method. AIP Conference Proceedings, 1493, 91-95. http://dx.doi.org/10.1063/1.4765475
[14]	Bulut, H., Baskonus, H.M. and Tuluce, S. (2013) Homotopy Perturbation Sumudu Transform Method for Heat Equations. Mathematics in Engineering, Science and Aerospace (MESA), 4, 49-60.
[15]	Chen, Y., Wang, Q. and Li, B. (2004) A Series of Soliton-Like and Double-Like Periodic Solutions of a (2 + 1)-Dimensional Asymmetric Nizhnik-Novikov-Vesselov Equation. Communications in Theoretical Physics, 42, 655-660. http://dx.doi.org/10.1088/0253-6102/42/5/655
[16]	Yomba, E. (2006) The Modified Extended Fan Sub-Equation Method and Its Application to the (2 + 1)-Dimensional Broer-Kaup-Kupershmidt Equation. Chaos, Solitons & Fractals, 27, 187-196. http://dx.doi.org/10.1016/j.chaos.2005.03.021
[17]	Motsa, S.S., Sibanda, P. and Shateyi, S. (2010) A New Spectral-Homotopy Analysis Method for Solving a Nonlinear Second Order BVP. Communications in Nonlinear Science and Numerical Simulation, 15, 2293-2302. http://dx.doi.org/10.1016/j.cnsns.2009.09.019
[18]	Motsa, S.S., Sibanda, P., Awad, F.G. and Shateyi, S. (2010) A New Spectral-Homotopy Analysis Method for the MHD Jeffery-Hamel Problem. Computers & Fluids, 39, 1219-1225. http://dx.doi.org/10.1016/j.compfluid.2010.03.004
[19]	Gardner, L.R., Gardner, G.A. and Dogan A. (1996) A Least-Squares Finite Element Scheme for RLW Equation. Communications in Numerical Methods in Engineering, 12, 795-804. http://dx.doi.org/10.1002/(SICI)1099-0887(199611)12:11<795::AID-CNM22>3.0.CO;2-O
[20]	Alam, M.N. and Akbar, M.A. (2013) Exact Traveling Wave Solutions of the KP-BBM Equation by Using the New Approach of Generalized (G’/G)-Expansion Method. SpringerPlus, 2, 617. http://dx.doi.org/10.1186/2193-1801-2-617
[21]	Alam, M.N., Akbar, M.A. and Mohyud-Din, S.T. (2014) General Traveling Wave Solutions of the Strain Wave Equation in Microstructured Solids via the New Approach of Generalized (G’/G)-Expansion Method. Alexandria Engineering Journal, 53, 233-241. http://dx.doi.org/10.1016/j.aej.2014.01.002
[22]	Alam, M.N. and Akbar, M.A. (2014) The New Approach of Generalized (G’/G)-Expansion Method for Nonlinear Evolution Equations. Ain Shams Engineering Journal, 5, 595-603. http://dx.doi.org/10.1016/j.asej.2013.12.008
[23]	Alam, M.N. and Akbar, M.A. (2014) Traveling Wave Solutions for the mKdV Equation and the Gardner Equation by New Approach of the Generalized (G’/G)-Expansion Method. Journal of the Egyptian Mathematical Society, 22, 402-406. http://dx.doi.org/10.1016/j.joems.2014.01.001
[24]	Zhang, J., Jiang, F. and Zhao, X. (2010) An Improved (G’/G)-Expansion Method for Solving Nonlinear Evolution Equations. International Journal of Computer Mathematics, 87, 1716-1725. http://dx.doi.org/10.1080/00207160802450166
[25]	Inc, M. and Evans, D.J. (2004) On Traveling Wave Solutions of Some Nonlinear Evolution Equations. International Journal of Computer Mathematics, 8, 191-202. http://dx.doi.org/10.1080/00207160310001603307
[26]	Hu, J.L. (2004) A New Method of Exact Traveling Wave Solution for Coupled Nonlinear Differential Equations. Physics Letters A, 322, 211-216. http://dx.doi.org/10.1016/j.physleta.2004.01.074
[27]	Fan, E.G. (2000) Extended Tanh-Function Method and Its Applications to Nonlinear Equations. Physics Letters A, 277, 212-218. http://dx.doi.org/10.1016/S0375-9601(00)00725-8
[28]	El-Wakil, S.A. and Abdou M.A. (2007) New Exact Travelling Wave Solutions Using Modified Extended Tanh-Function Method. Chaos, Solitons & Fractals, 31, 840-852. http://dx.doi.org/10.1016/j.chaos.2005.10.032
[29]	Alam, Md.N. and Belgacem, F.B.M. (2016) New Generalized (G’/G)-Expansion Method Applications to Coupled Konno-Oono Equation. Advances in Pure Mathematics, 6, 168-179. http://dx.doi.org/10.4236/apm.2016.63014
[30]	Alam M.N., Akbar, M.A. and Mohyud-Din, S.T. (2014) A Novel (G’/G)-Expansion Method and Its Application to the Boussinesq Equation. Chinese Physics B, 23, Article ID: 020203. http://dx.doi.org/10.1088/1674-1056/23/2/020203
[31]	Alam, M.N., Hafez, M.G., Belgacem, F.B.M. and Akbar, M.A. (2015) Applications of the Novel (G’/G)-Expansion Method to Find New Exact Traveling Wave Solutions of the Nonlinear Coupled Higgs Field Equation. Nonlinear Studies, 22, 613-633.
[32]	Alam, M.N., Belgacem, F.B.M. and Akbar, M.A. (2015) Analytical Treatment of the Evolutionary (1 + 1)-Dimensional Combined KdV-mKdV Equation via the Novel (G’/G)-Expansion Method. Journal of Applied Mathematics and Physics, 3, 1571-1579. http://dx.doi.org/10.4236/jamp.2015.312181
[33]	Alam, M.N., Belgacem, F.B.M. (2015) Application of the Novel (G’/G)-Expansion Method to the Regularized Long Wave Equation. Waves, Wavelets and Fractals, 1, 51-67. http://dx.doi.org/10.1515/wwfaa-2015-0006
[34]	Alam, M.N. and Akbar, M.A. (2014) Traveling Wave Solutions of the Nonlinear (1 + 1)-Dimensional Modified Benjamin-Bona-Mahony Equation by Using Novel (G’/G)-Expansion Method. Physical Review & Research International, 4, 147-165.
[35]	Bulut, H., Baskonus, H.M. and Tuluce, S. (2014) On the Solution of Nonlinear Time-Fractional Generalized Burgers Equation by Homotopy Analysis Method and Modified Trial Equation Method. International Journal of Modeling and Optimization, 4, 305-309. http://dx.doi.org/10.7763/IJMO.2014.V4.390
[36]	Bekir, A. (2008) Application of the (G’/G)-Expansion Method for Nonlinear Evolution Equations. Physics Letters A, 372, 3400-3406. http://dx.doi.org/10.1016/j.physleta.2008.01.057
[37]	Smaoui, N. and Belgacem, F.B.M. (2002) Connections between the Convective Diffusion Equation and the Forced Burgers Equation. Journal of Applied Mathematics and Stochastic Analysis, 15, 57-75. http://dx.doi.org/10.1155/S1048953302000060
[38]	Zayed, E.M.E. (2011) The (G’/G)-Expansion Method Combined with the Riccati Equation for Finding Exact Solutions of Nonlinear PDEs. Journal of Applied Mathematics & Informatics, 29, 351-367.
[39]	Zhu, S. (2008) The Generalized Riccati Equation Mapping Method in Nonlinear Evolution Equation: Application to (2 + 1)-Dimensional Boiti-Pempinelle Equation. Chaos, Solitons & Fractals, 37, 1335-1342. http://dx.doi.org/10.1016/j.chaos.2006.10.015