Iterative Technology in a Singular Fractional Boundary Value Problem with q -Difference

Xiuli Lin, Zengqin Zhao^*, Yongliang Guan

School of Mathematical Sciences, Qufu Normal University, Qufu, China.

DOI: 10.4236/am.2016.71008                

Abstract

In this paper, we apply the iterative technology to establish the existence of solutions for a fractional boundary value problem with q-difference. Explicit iterative sequences are given to approxinate the solutions and the error estimations are also given.

Keywords

Fractional Boundary Value Problem with q-Difference, Iterative Sequence, Green’s Function, Error Estimation

Received 19 December 2015; accepted 23 January 2016; published 26 January 2016

1. Introduction

This paper deals with the existence of solutions for the following fractional boundary value problem with q-difference

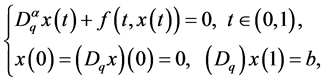(1.1)

where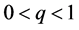, 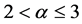and 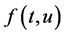may be singular at (and/or).

For problem (1.1), there have been paid attention to the existences of solutions. Rui [1] investigated the exi- stence of positive solutions by applying a fixed point theorem in cones. By fixed point theorem again, Li and Han [2] considered a similar fractional q-difference equations given as

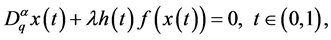
subject to the boundary conditions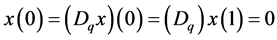. In this work, we will apply the iterative technology ( [9] [11] [14] ), and as far as we know, there are few papers to establish the existence of solutions by the iterative technology for the boundary value problem with q-difference.

Motivated by the work mentioned above, with the iterative technology and properties of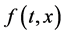, explicit iterative sequences are given to approximate the solutions and the error estimations are also given.

2. Preliminaries and Some Lemmas

In this section, we introduce some definitions and lemmas.

Definition 2.1 [1] . Let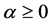, 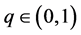and f be a function defined on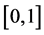. The fractional q-integral of the Riemann-Liouville type is defined by and

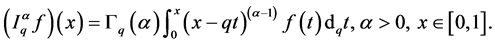
The q-integral of a function f defined in the interval 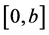is given by

and q-integral of higher order is defined by

Remark 1:,. The q-gamma function is defined by , , and satisfies, where,.

Definition 2.2 [1] . Let,. The fractional q-derivative of the Riemann-Liouville type of order

is defined by and

where m is the smallest integer greater than or equal to. The q-derivative of a function f is defined by

and q-derivatives of higher order by

Lemma 2.1 [1] . Suppose and is q-integrable on. Then the boundary value problem

has the unique solution

where

(2.1)

(2.2)

Lemma 2.2 [1] . Function G defined as (2.2). Then G satisfies the following properties:

(1), and for all.

(2) for all.

Lemma 2.3. Function G defined as (2.2). Then

Proof. Note that (2.2) and, it follows that for all. This, with Lemma 2.2, implies that

3. Main Result

First, for the existence results of problem (1.1), we need the following assumptions.

(A₁) is continuous.

(A₂) For, f is non-decreasing respect to x and for any, there exists a constant such that

(3.1)

Then, we let the Banach space, and

Clearly P is a normal cone and Q is a subset of P in the Banach space E.

In what follows, we define the operator

(3.2)

where are given by (2.1) and (2.2).

Now, we are in the position to give the main results of this work.

Theorem 3.1. Suppose (A₁), (A₂) hold. Then problem (1.1) has at least one positive solution in Q if

(3.3)

Proof. We shall prove the existence of solution in three steps.

Step 1. The operator T defined in (3.2) is.

For any, there exists a positive constant such that

Then from (A₂): is non-decreasing respect to x and (3.1), we can imply that for

(3.4)

where

is implied by the equivalent form to (3.1): if,

From (3.4) and Lemma 2.3, we can have

and

where:

This implies T is.

Step 2. There exist iterative sequences, satisfying

Since for, there exists a constant such that

(3.5)

For defined in (3.5), there exist constants satisfying

(3.6)

Let

(3.7)

(3.8)

Then it follows that

In fact, from (3.6)-(3.8) , we have

(3.9)

(3.10)

(3.11)

Then, by (3.9)-(3.11), (A₂) and induction, the iterative sequences, satisfy

Step 3. There exists such that

Note that. By induction it is easy to obtain

Thus, for we have

(3.12)

This yields that there exists such that

Moreover, from (3.12) and

we have

Letting in (3.8), is a fixed point of T. That is, is a positive solution of problem (1.1).

Theorem 3.2. Suppose the conditions hold in Theorem 3.1. Then for any initial, there exists a se- quence such that uniformly on as, where is the positive solu- tion of problem (1.1). And the error estimation for the sequence is

(3.13)

where k is a constant with and determined by.

Proof. Let be given. Then there exists a constant such that

(3.14)

For defined in (3.14), choose constants such that

Then define as (3.7), (3.8), and we can have converges uniformly to the positive solution of problem (1.1) on as.

For the error estimation (3.13), it can be obtained by letting in (3.12).

Example 3.3. Consider the function

satisfies (A₂) and is singular at. Let,. Then

By Theorem 3.1, the following problem

has at least one positive solution.

Acknowledgements

The author is grateful to the referees for their valuable comments and suggestions.

Support

Project supported by Program for Scientific research innovation team in Colleges and universities of Shandong Province, the Doctoral Program Foundation of Education Ministry of China (20133705110003), the Natural Science Foundation of Shandong Province of China (ZR2014AM007), the Natural Science Foundation of China (11571197).

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Ferreira, R.A.C. (2011) Positive Solutions for a Class of Boundary Value Problems with Fractional q-Differences. Computers and Mathematics with Applications, 61, 367-373. http://dx.doi.org/10.1016/j.camwa.2010.11.012
[2]	Li, X., Han, Z. and Li, X. (2015) Boundary Value Problems of Fractional q-Difference Schröinger Equations. Applied Mathematics Letters, 46, 100-105. http://dx.doi.org/10.1016/j.aml.2015.02.013
[3]	Ferreira, R. (2011) Positive Solutions for a Class of Boundary Value Problems with Fractional q-Differences. Computers & Mathematics with Applications, 61, 367-373. http://dx.doi.org/10.1016/j.camwa.2010.11.012
[4]	Li, X., Han, Z. and Sun, S. (2013) Existence of Positive Solutions of Nonlinear Fractional q-Difference Equation with Parameter. Advances in Difference Equations, 2013, 260. http://dx.doi.org/10.1186/1687-1847-2013-260
[5]	Al-Salam, W.A. (1966-1967) Some Fractional q-Integrals and q-Derivatives. Proceedings of the Edinburgh Mathematical Society, 15, 135-140. http://dx.doi.org/10.1017/S0013091500011469
[6]	Agarwal, R.P. (1969) Certain Fractional q-Integrals and q-Derivatives. Proceedings of the Cambridge Philosophical Society, 66, 365-370. http://dx.doi.org/10.1017/S0305004100045060
[7]	Rajkovic, P.M., Marinkovic, S.D. and Stankovic, M.S. (2007) Fractional Integrals and Derivatives in q-Calculus. Applicable Analysis and Discrete Mathematics, 1, 311-323. http://dx.doi.org/10.2298/AADM0701311R
[8]	Jankowski, T. (2014) Boundary Problems for Fractional Differential Equations. Applied Mathematics Letters, 28, 14-19. http://dx.doi.org/10.1016/j.aml.2013.09.004
[9]	Mao, J., Zhao, Z. and Xu, N. (2010) On Existence and Uniqueness of Positive Solutions for Integral Boundary Boundary Value Problems. Electronic Journal of Qualitative Theory of Differential Equations, 16, 1-8. http://dx.doi.org/10.14232/ejqtde.2010.1.16
[10]	Guo, D.J. and Lakshmikantham, V. (1988) Nonlinear Problems in Abstract Cones. Academic Press, Boston.
[11]	Zhang, X., Liu, L. and Wu, Y. (2012) The Eigenvalue Problem for a Singular Higher Order Fractional Differential Equation Involving Fractional Derivatives. Applied Mathematics and Computation, 218, 8526-8536. http://dx.doi.org/10.1016/j.amc.2012.02.014
[12]	Liu, Y., Zhang, W. and Liu, X. (2012) A Sufficient Condition for the Existence of a Positive Solution for a Nonlinear Fractional Differential Equation with the Riemann-Liouville Derivative. Applied Mathematics Letters, 25, 1986-1992. http://dx.doi.org/10.1016/j.aml.2012.03.018
[13]	Vong, S. (2013) Positive Solutions of Singular Fractional Equations with Integral Boundary Conditions. Mathematical and Computer Modelling, 57, 1053-1059. http://dx.doi.org/10.1016/j.mcm.2012.06.024
[14]	Lin, X. and Zhao, Z. (2013) Existence and Uniqueness of Symmetric Positive Solutions of 2n-Order Nonlinear Singular Boundary Value Problems. Applied Mathematics Letters, 26, 692-698. http://dx.doi.org/10.1016/j.aml.2013.01.007