An Entropy Approach to the Natures of the Electric Charge and Magnetic Flux ()
1. Introduction
Generally, flows in thermodynamic systems are driven by forces; i.e. flows and forces occur in conjugate pairs. That is, heat flow is driven by differences in temperature between the system and its surroundings, volume flow by differences in pressure, electric charge flow by differences in electrical potential, magnetic flux is a flow driven by magnetic potential, and mass flow by differences in concentration [1] .
The second law of thermodynamics provides a rule that describes the direction of change in a system in the absence of external forces. It depends on natural evidence that heat flows from warm objects to cold objects, that objects fall downward in a gravity field, that electric current flows from high potential to low potential, the magnetic flux emerges from magnets of high magnetic potential to iron rods of zero magnetic potential and solutes diffuse from regions of high concentration into regions of low concentration. So, the second law is a rule which captures these facts in a remarkably concise way [2] . Essential to the second law of thermodynamics is the idea of a reversible flow. A flow is reversible when it is driven by an infinitesimal force, i.e. a force which is so close to zero that a small change in the magnitude of the force at the appropriate place can reverse the direction of the flow [3] . In real systems, flows are almost always irreversible, for example flow of heat into an ice cube from a glass of warm water which occurs between a substantial temperature difference, or the flow of electric current through a lamp which occurs across a substantial electrical potential difference or the flow of magnetic flux from a magnet of high magnetic potential to piece of iron. Such processes are irreversible and lead to increase the entropy of the universe [4] .
In the following analysis, the reversible change of heat into electric current will be studied as implemented through the definition of thermoelectric effects [5] . Then, it will be studied the interchangeability of heat into magnetic flux and the interchangeability of electric current into magnetic flux and vice versa through mathematical and experimental analysis. Such similarities will be introduced to modify the second law of thermodynamics to include the electric and magnetic energies as sources of increase of entropy similar to heat. Accordingly, it will be tried modifications of the Maxwell’s wave equations to define the nature of the electric charge and magnetic flux as electromagnetic waves, similar to the heat flux, but of different potentials.
2. Interchangeability of Heat and Electric Current
Thermoelectricity is defined as the direct conversion of heat into electric energy, or vice versa [5] . The thermoelectric effect is also defined in literature as a phenomenon by which a temperature difference is directly converted to electric potential and vice versa [6] . Such definitions indicate in general a reversible conversion of electricity into heat and vice versa. It means also the difference between the flow of heat and of the flow of electric current is the potential of each flow. Replacing the thermal potential by an electric potential converts the flow of heat into a flow of electric current or vice-versa. Accordingly, both flows should have the same nature as proved by discoveries of Joule, Seebeck, Peltier, and Thomson. According to Joule's law, a conductor carrying a current generates heat at a rate proportional to the product of the resistance (R) of the conductor and the square of the flowing current (I) [7] . The German physicist Thomas J. Seebeck discovered in the 1820s that if a closed loop is formed by joining the ends of two strips of dissimilar metals and the two junctions of the metals are at different temperatures, an electromotive force, or voltage, arises that is proportional to the temperature difference between the junctions [8] . Such circuit of this type is called a thermocouple; a number of thermocouples connected in series are called a thermopile [9] . In 1834, the French physicist Jean C. A. Peltier discovered an effect inverse to the Seebeck effect: If a current passes through a thermocouple, the temperature of one junction increases and the temperature of the other decreases, so that heat is transferred from one junction to the other [10] . The rate of heat transfer is proportional to the current and the direction of transfer is reversed if the current is reversed. The Scottish scientist William Thomson (later Lord Kelvin) discovered in 1854 that if a temperature difference exists between any two points of a current-carrying conductor, heat is either evolved or absorbed depending upon the material [11] . If heat is absorbed by such a circuit, then heat may be evolved if the direction of the current or of the temperature gradient is reversed [12] . It had been shown that the Seebeck effect is a result of the combined Peltier and Thomson effects. Many devices based on thermoelectric effects are used to measure temperature, generate heat from electric current or generate electricity from flowing heat [13] .
The equivalence of electric energy and thermal energy as concluded from the definition of the thermoelectric effect is also proved by the applications of the Seebeck effect in thermoelectric generators and of Peltier effect in thermoelectric refrigerators [14] . However, the similarity of the natures of heat and electric current is indicated also by the analogy of the laws that characterize their flows through conductors where the thermal potential is analogous to the electric potential and the flow of electric charges is analogous to the flow of heat.
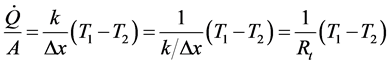 (1)
(1)
 (2)
(2)
3. Interchangeability of Heat and Magnetic Flux
A simple experiment had been elaborated to prove interchangeability of heat and magnetic (or mechanical) energy, and the equivalence of the grades of the thermal energy, or heat, and the magnetic energy. Figure 1 shows a permanent magnet immersed in an insulted water basin and was allowed to attract polished iron balls along an inclined smooth glass plane. The temperature of water was initially recorded. As the magnet performed a mechanical work, a decrease in the water temperature was measured by a digital thermometer Figure 2. By applying the first law of thermodynamics on the magnet-water closed-system [17] , we get the following equation:
 (3)
(3)
![]()
Figure 1. Measurement of magnet’s work during attraction of iron balls.
![]()
Figure 2. Measurement and calculation results of the system temperature. (Experimental data: thermal capacity of the flask = 1.26 kJ/ deg, mass of each iron ball = 0.3 kg, number of ttracted balls per minute = 42 balls, s = 20 and j = 30 deg.).
the magnetocaloric effect which is defined as the heating or cooling of a magnetic material due to the application of a magnetic field [18] . The magnetic potential in such applications is replaced by thermal potential. This effect has been called adiabatic demagnetisation for years which is considered as a phenomenon and represents a practical application of the magnetocaloric effect in magnetic materials [19] . So, the thermal energy can be converted into mechanical energy and vice versa. Such results prove that the heat has an equivalent grade as to the magnetic energy and both should be similar.
4. Interchangeability of Electric Energy and Magnetic Energy
Reviewing Faraday’s experiment of magnetic induction, it is possible to prove the similarity of the natures of the flow of electric current and the flow of magnetic flux. Figure 3 shows Faraday’s apparatus that demonstrates interactions between magnetic and electric fluxes [20] . When the shown switch is closed, a magnetic field is emitted from the coil on the top part of the iron ring, called as a primary coil, and is transmitted to the coil on the bottom part of the ring which is called as a secondary coil. The galvanometer is used to detect any current induced in the secondary coil. It was found that each time the switch is closed; the galvanometer detects a current in one direction in the secondary coil. Each time the switch is opened, the galvanometer detects also a current in the opposite direction. Interestingly, if the switch remains closed or open for any length of time, there is no current through the galvanometer.
Available literature defines the electric current as a flow of electrons and defines the magnetic flux as the quantity of magnetic field that penetrates an area at right angles [21] . According to this definition of electric current; the flow of its electrons in the primary coil should induce, by analogy between the electric current and magnetic flux, a flow of some other particles in the iron ring. Similarly, if the magnetic flux that passes through the secondary coil is defined as the quantity of magnetic field that penetrates an area at right angles, then it should not regenerate a flow of particles in the secondary coil as both have different natures. So, the demonstrated Faraday’s experiment shows that the conversion of electric energy into magnetic energy in the primary coil is done by replacing the electric potential of the electric energy by magnetic potential and the conversion of the magnetic energy into electric energy in the secondary coil is done by replacing the magnetic potential by electric potential. It means that both fluxes should have similar natures so that both can be interchanged alternatively.
5. Entropy and the Second Law of Thermodynamics
The previously proved interchangeabilities of heat, electric current and magnetic flux prove the equivalence of their grades and the similarity of their natures. However, the second law defines a new state function, the entropy that may describe the irreversibilities of heat flow when dealing with the entropy of the universe rather than the entropy of a system as a state function. For reversible processes the heat flow is expressed as the product of temperature, as the force that derives the heat flow, times the increase of the entropy of the system associated by the heat flow [22] .
 (4)
(4)
Equation (4) is used to represent the heat added to a system T-s property diagram seen in Figure 4.
However, the total changes in entropy (system plus surroundings) for reversible process where the same heat is transferred through infinitesimally small difference [23]
![]()
Figure 3. Faraday’s apparatus for demonstrating the interactions between electric and magnetic energies [11] .
![]()
Figure 4. Heat representation in a T-s property diagram.
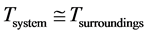 ,
,
 (5)
(5)
So, the total change in entropy for a reversible process is zero as the entropy is a state function. However, for real processes where the temperature of the system should be higher than the temperature of surroundings [24]
 (6)
(6)
So, we get
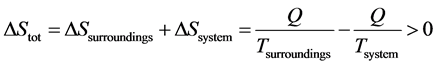
So, in any physical process, the entropy S for an isolated system never decreases; that is, we have
 always (7)
always (7)
Reviewing the electric energy, we find also that the current will flow from high potential to low potential.
According to the similarity of heat, electric energy and magnetic energy, such principle of increase of entropy should include also the increase of entropy of the universe due to transfer of all these energies. So, we should the following relation between the electrical potential of the system “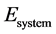 ”and of the surroundings “
”and of the surroundings “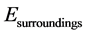 ”, similar to the relation in Eq. (6) between the temperatures of the system and surroundings:
”, similar to the relation in Eq. (6) between the temperatures of the system and surroundings:
![]() (8)
(8)
Accordingly; there is an increase of entropy of the universe associated by the flow of electric current and, by similarity, of magnetic flux that leads also to apply Equation (7) [24] .
So, the second law should consider the energies similar to the heat as the flow of electric charges and magnetic flux as sources of similar irreversibilities. In other words, the flow of electric charge and magnetic flux should be associated also by an increase of entropy of a system and expressed by a similar equation as (4). Hence, the reversible transfer of electric current should be expressed as the product of the electric potential times the increase of entropy associated by the flow of electric charge and the magnetic flux as the product of the magnetic potential times the increase of entropy associated by the flow of magnetic flux according to the following equations:
![]() (9)
(9)
![]() (10)
(10)
Equations (9) and (10) were the foundations that were previously introduced to find a fundamental energy equation that embraces the flow of heat, electric current and magnetic flux which was applied in many citations in the following form [25] - [28] :
![]() (11)
(11)
According to Equations (4), (9), (10), and (11) entropy can be defined as a measure of energizing, or disordering, the molecules of a system by thermal, electric or magnetic energies. The postulate that the flow of electric current is associated by flow of entropy was early discovered by Einstein and his colleagues [29] . However, as the heat is represented in the T-s diagram by the area down the process line as seen in a T-s property diagram as shown in Figure 4 [4] , the electric energy can be represented also by an area in an E-s property diagram as seen in Figure 5 and the magnetic energy can be represented also by the area in an H-s property diagram as seen in Figure 6.
However, relying on the definition of entropy of a system in terms of its statistical concept according to Ludwig Boltzmann as follows [30] :
![]() (12)
(12)
![]() : Boltzmann’s constant = 1.38 × 10−23,
: Boltzmann’s constant = 1.38 × 10−23, ![]() is the number of arranging the microstates of a system at specified total internal energy. According to Equation (12), Boltzmann introduced a statistical concept of entropy. He showed also that the arrow of time was statistical in origin and he sought to derive the Second Law of Ther-
is the number of arranging the microstates of a system at specified total internal energy. According to Equation (12), Boltzmann introduced a statistical concept of entropy. He showed also that the arrow of time was statistical in origin and he sought to derive the Second Law of Ther-
![]()
Figure 5. Electric Energy representation in an E-s property diagram.
![]()
Figure 6. Magnetic energy representation in a H-s property diagram.
modynamics from the statistical behavior of a large number of molecules obeying the simple laws of mechanics, namely the conservation of momentum and energy. Such analysis was given the name statistical mechanics [31] . Considering such point of view, the task of explaining the arrow of time only through entropy generation due to reversible and irreversible processes looks like the task of finding some simple relations which obliquely “cause” entropy to increase with high probability. According to the statistical definition of entropy as introduced by Boltzmann, the reversible flow of thermal, electric and magnetic energies should lead also to the increase entropy [32] .
6. The Maxwell’s Equations in an Energy Frame of Reference
The representation of energy, or heat, as flow of electromagnetic waves is defined mathematically by Maxwell’s equations. However, it is expressed in literature in terms of flow of electric energy wave in an E-t plane, and magnetic energy wave in an H-t plane as follows [33] :
![]() (13)
(13)
![]() (14)
(14)
where c is the speed of light in the medium, in vacuum c = c0 = 299,792,458 meters per second. Replacing the time in the previous Maxwell’s equations by entropy, Maxwell’s equations may be represented in an energy frame of reference composed of the coordinates E-H-s as seen in Figure 7. The areas scanned by the electric and magnetic waves in such frame express actually the flow of electric and magnetic energies as components of the flowing electromagnetic wave as seen in Figure 5 and Figure 6. So, the modified form of Maxwell’s relation casted into an energy frame of reference that replaces the time by an energy property, the entropy, will be as follows [34] :
![]() (15)
(15)
![]() (16)
(16)
Replacement of time by entropy sustains Eddington argument of the arrow of time as indication of the direction of progressive increase of random elements in nature and his lengthy conclusion that such randomness is a property of entropy alone which is also a measure of randomness in time [35] . Such fuzzy approach realizes a dream of Tesla (1856-1943) who searched the transformation of the wave equations as described by James Clerk Maxwell (1831-1879) into an energy frame of reference that expresses the flow of energy associated by the flow of electromagnetic waves [36] .
![]()
Figure 7. Flow of electromagnetic waves in an energy frame of reference that shows the electric energy flow in an electric field―entropy plane and the magnetic energy flow into a magnetic field―entropy plane [34] .
According to the indicated representation of the electromagnetic waves in the introduced coordinate system, the bounded or shaded areas by the wave lines in the E-s and H-s planes of Figure 7 represent the imparted flow of energy. Denoting the imparted energy per an electromagnetic wave by the symbol “Ћ” Joule/wave, it is possible to mathematically estimate such energy or shaded areas as follows [37] :
![]() (17)
(17)
Accordingly, it is possible to calculate the energy flow per unit time as follows:
![]() Watt (18)
Watt (18)
“v” is the frequency of the electromagnetic wave, or the number of waves per unit time. This means that the energy quantization is stemmed mainly from its nature as a wave. Such understanding is a direct conclusion of representing the flow of electromagnetic waves in the introduced energy frame of reference.
7. The Nature of Electric Charge and Magnetic Flux
The previously proved interchangeabilities between thermal energy and electric energy, thermal energy and magnetic energy and between electric energy and magnetic energy prove that the heat flux, electric current and magnetic flux should have the same nature. So, if the primary form of heat flux is a flow of thermal radiation as electromagnetic waves of thermal potential, we may postulate the electric current is a flow of electromagnetic waves of electric potential and the magnetic flux as electromagnetic waves of magnetic potential.
The representation of heat, as flow of electromagnetic waves, is defined mathematically by Maxwell’s equations and is represented graphically in Figure 7. According to the discussed similarity of flow of thermal radiation as defined by the modified Maxwell’s wave equation Equations (15) and (16) and the electric current; the electric charge can be defined as a special solution of the Maxwell’s equations as flow of electromagnetic waves whose electric component oscillates initially around a specific positive or negative potential “![]() ,” while its magnetic component oscillates around zero potential. Such solution is presented mathematically as follows [38] :
,” while its magnetic component oscillates around zero potential. Such solution is presented mathematically as follows [38] :
![]() (19)
(19)
![]() (20)
(20)
Equations (19) and (20) represent a solution of Maxwell’s electromagnetic wave equations of specific initial conditions that define the flow of electric charges as a flow of ionized electromagnetic waves which have a non-zero electric potential. Such solution can be represented graphically as seen in Figure 8. In case of Figure 8, the net energy imparted per wave will be energy of net negative potential-![]() , in other words a negatively charged energy, which can be calculated as follows:
, in other words a negatively charged energy, which can be calculated as follows:
![]() (19)
(19)
Such definition of electric charge or current as electromagnetic waves of electric potential found plausible explanation of the discovered Tesla’s “Radiant Energy” or Tesla’s “Dark Waves” as normal transfer of electric current, of wave-nature, through air by the high electric potential of Tesla’s tower [39] . Such postulated nature of electric charge succeeds also in solving the duality confusion in the field of electrodynamics [40] .
According to the discussed similarity of the natures of the flow of thermal radiation as defined by the modified Maxwell’s wave equation Equations (15) and (16) and the magnetic flux; the magnetic flux can be defined as a special solution of such equations by defining magnetic flux as flow of electromagnetic waves whose magnetic component oscillates initially around a specific positive or negative potential “![]() ”, while its electric component oscillates around zero potential as seen in Figure 9. Such solution is presented mathematically as follows:
”, while its electric component oscillates around zero potential as seen in Figure 9. Such solution is presented mathematically as follows:
![]() (17)
(17)
![]()
![]()
Figure 8. Flow of electric charges as E. M. waves of negative ele- ctric potential.
![]()
Figure 9. Flow of magnetic flux as E. M. waves of negative magnetic potential.
Such definition of the nature of magnetic flux as electromagnetic waves of magnetic potential found a plausible explanation of the MIT discovery of wireless power transmission by magnetic resonant coupling which was identified as “evanescent waves”. Such waves can be plausibly defined as wireless transfer of normal magnetic flux, of wave-nature, through air by the high potential of the discovered magnetic resonant coupling [41] . Similarly, it helps to find a simple universal system of units that solves the complexities if the SI system of units in the field of electrodynamics [42] .
8. Conclusion
Reviewing the natural flow of electric charges from high electric potential to low potential and the natural flow of magnetic flux from high magnetic potential to low potential which are similar to the natural flow of heat from high temperature to low temperature, it is possible to prove in this study that transfer of electric charge and magnetic flux represent sources of irreversibility and should be considered as a source of increase of entropy of the universe similar to the transfer of heat. Such results help through a followed entropy approach in defining the nature of the electric charge as electromagnetic wave of electric potential and the nature of magnetic flux as electromagnetic waves of magnetic potential similar to the heat flux as electromagnetic waves of thermal potential. Such postulated natures of electric charge and magnetic flux find plausible explanations of the Tesla dark waves, the MIT evanescent waves, solves the duality confusion and find a simple universal system of units that solves the complexities of the SI system of units in the field of electrodynamics. It also explains the speed of flow of the electric charges that approaches the velocity of light.
NOTES
*Corresponding author.