1. Introduction
Approximating the solutions of the system of linear and nonlinear equations has widespread applications in applied mathematics [1] -[11] . Many techniques including homotopy perturbation method (HPM) [12] and iterative methods [13] were suggested to search for the solution of linear systems. In 2009 Keramati [2] and in 2011 Liu [3] in their articles applied HPM to the solution of the system . In this article we used homotopy analysis method [14] [15] with different H(x) to solve linear system
. In this article we used homotopy analysis method [14] [15] with different H(x) to solve linear system  and showed that our results were better than the HPM results; then convergence of the method was considered.
and showed that our results were better than the HPM results; then convergence of the method was considered.
Consider a linear system
 (1)
(1)
where  is nonsingular and
is nonsingular and  is a vector.
is a vector.
First of all, the basic ideas of the homotopy analysis method are being discussed.
Let  be an initial guess of x, and
be an initial guess of x, and  be called the embedding parameter. The homotopy analysis method is based on a kind of continuous mapping
be called the embedding parameter. The homotopy analysis method is based on a kind of continuous mapping  such that, as the embedding parameter q increases from 0 to 1,
such that, as the embedding parameter q increases from 0 to 1,  varies from the initial guess
varies from the initial guess  to the exact solution x. To ensure this, choose such an auxiliary linear operator as
to the exact solution x. To ensure this, choose such an auxiliary linear operator as
 (2)
(2)
and we define the operator
 (3)
(3)
Let 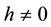 and
and  denote the so-called auxiliary parameter and auxiliary matrix, respectively. Using the embedding parameter
denote the so-called auxiliary parameter and auxiliary matrix, respectively. Using the embedding parameter , we construct a family of equations
, we construct a family of equations

from (2) and (3) we have
![]() (4)
(4)
Obviously, at q = 0 and q = 1, one has ![]() and
and ![]() respectively. Thus, as q increases from 0 to 1,
respectively. Thus, as q increases from 0 to 1, ![]() varies continuously from
varies continuously from ![]() to x. Such kind of continuous variation is called deformation in topology [16] . We call the family of equations like (4) the zeroth-order deformation equation. Now we define mth-order deformation derivative
to x. Such kind of continuous variation is called deformation in topology [16] . We call the family of equations like (4) the zeroth-order deformation equation. Now we define mth-order deformation derivative
![]() (5)
(5)
where ![]() Because
Because ![]() is now a function of the embedding parameter q, by Taylors Theorem, we expand
is now a function of the embedding parameter q, by Taylors Theorem, we expand ![]() in a power series of the embedding parameter q as follows:
in a power series of the embedding parameter q as follows:
![]()
By using (5) we have
![]() (6)
(6)
If the series (6) is convergent at q = 1, then using the relationship ![]() one has the series solution
one has the series solution
![]() (7)
(7)
Now we have the so-called mth-order deformation equation
![]() (8)
(8)
where
![]() (9)
(9)
and
![]() (10)
(10)
By using (2) we obtain
![]() (11)
(11)
Also by using (3) and (9) we have
![]()
and then
![]()
Finally by using (11) we obtain
![]() (12)
(12)
Now with the initial guess ![]() and
and ![]() we have
we have
![]() (13)
(13)
hence, by substituting (13) in (7) we obtain
![]() (14)
(14)
and by factor of ![]() we have
we have
![]() (15)
(15)
Now we have to prove the convergence of (15).
Theorem 1. The sequence ![]() is a Cauchy sequence if
is a Cauchy sequence if
![]()
Proof: Following ([2] , Theorem 1) we have to show that
![]()
Now considering
![]()
then
![]()
let ![]() then
then
![]()
so we have
![]()
since ![]() then we obtain
then we obtain
![]()
which completes the proof.
2. Main Results
In this section For solving the linear system (1) we apply different H(x) and the convergence of the method is checked. At first assume that A is a nonsingular diagonally dominate matrix and ![]() Dividing (1) by
Dividing (1) by ![]() and without loss of generality we can obtain
and without loss of generality we can obtain
![]() (16)
(16)
where![]() , such that
, such that
![]() (17)
(17)
and
![]()
Now we apply different H(x) and the convergence of the method is tested.
1) we propose ![]() with
with
![]() (18)
(18)
and show that
![]()
Theorem 2. If A is diagonally dominated and![]() , where
, where ![]() is defined in (17) then
is defined in (17) then
![]()
Proof: By direct calculation we have
![]()
and first row is satisfied:
![]()
Since A is diagonally dominated, B is diagonally dominated and we have
![]() (19)
(19)
Now by using (19) we obtain
![]()
This relation satisfis for other rows also and
![]()
2) We propose ![]() with
with
![]() (20)
(20)
and show that
![]()
Theorem 3. If A is diagonally dominated and![]() , where
, where ![]() is defined in (17) then
is defined in (17) then
![]()
Proof: Following Theorem (2)
![]()
such that
![]()
and last row is satisfied:
![]()
This relation satisfis for other rows also
![]()
3) We propose ![]() such that S and R was explained in (18) and (20) respectively and show that
such that S and R was explained in (18) and (20) respectively and show that
![]()
Theorem 4. If A is diagonally dominated and![]() , where
, where ![]() is defined in (17) then
is defined in (17) then
![]()
Proof: Similar to proof of Theorems (2) and (3).
4) We propose ![]() with
with
![]() (21)
(21)
![]()
and show that
![]()
Theorem 5. If A is diagonally dominated and![]() , where
, where ![]() is defined in (17) then
is defined in (17) then
![]()
Proof: Following Theorem (2) after expanding ![]() according to the first row we have
according to the first row we have
![]()
This relation satisfis for other rows also
![]()
5) We propose ![]() such that
such that ![]() and
and ![]() was explained in (21) and (20) respectively and show that
was explained in (21) and (20) respectively and show that
![]()
Theorem 6. If A is diagonally dominated and![]() , where
, where ![]() is defined in (17) then
is defined in (17) then
![]()
Proof: Similar to proof of Theorems (3) and (5).
6) We propose ![]() such that U is the strictly upper triangular part of A and show that
such that U is the strictly upper triangular part of A and show that
![]()
Theorem 7. If A is diagonally dominated and![]() , where
, where ![]() is defined in (17) then
is defined in (17) then
![]()
Proof: Following Theorem (2) after expanding ![]() according to the first row we have
according to the first row we have
![]()
This relation satisfis for other rows also
![]()
7) We propose ![]() such that U is the strictly upper triangular part of A and R was explained in (20) and show that
such that U is the strictly upper triangular part of A and R was explained in (20) and show that
![]()
Theorem 8. If A is diagonally dominated and![]() , where
, where ![]() is defined in (17) then
is defined in (17) then
![]()
Proof: Similar to proof of Theorems (3) and (7).
Now in the next section we apply ![]() for solving numerical examples.
for solving numerical examples.
3. Numerical Results
In this section, we present some numerical examples to apply HAM and HPM methods for solving linear system. We used of Matlab 2013 for numerical results.
Example 1. Consider the linear system![]() , that
, that ![]()
![]() and the exact solution is
and the exact solution is![]() .
.
Table 1 shows the iteration number,error,spectral radius of iteration matrix and computation time.
According to Table 1 we obtain the desirable result for solving this system by seven iterations with HAM and ![]() while by HPM method we used of fourteen iteration.
while by HPM method we used of fourteen iteration.
In this example the matrices S and ![]() are same and the results are same too.
are same and the results are same too.
Example 2. In this example we apply HAM method for solving the linear system
![]()
where A is a ![]() matrix, b is a
matrix, b is a ![]() vector that its components are sum of the row components of the corresponding matrix and the exact solution is
vector that its components are sum of the row components of the corresponding matrix and the exact solution is![]() . The numerical results are in Table 2.
. The numerical results are in Table 2.
![]()
Table 1. Camparision between HPM and HAM for 3 ´ 3 system.
![]()
Table 2. Camparision between HPM and HAM for 1000 ´ 1000 system.
4. Conclusion
From the numerical results, we have seen that the HAM method with different ![]() produces a spectral radius smaller than the HPM and with the less iteration we obtain the desirable result.
produces a spectral radius smaller than the HPM and with the less iteration we obtain the desirable result.
Acknowledgements
We thank Islamic Azad University for support researcher plan entitled: “Combination of Iterative methods and semi analytic methods for solving linear systems” and the Editor and the referee for their comments.
NOTES
*Corresponding author.