Improving Global Performance on GPU for Algorithms with Main Loop Containing a Reduction Operation: Case of Dijkstra’s Algorithm ()
1. Introduction
In this paper, we examine the impact of copying data on the global acceleration of an algorithm in which tasks are shared between CPU and GPU. We use Dijkstra’s algorithm on the shortest path [1] to illustrate the problem. Dijkstra’s algorithm has already been a subject of many parallel implementations on GPU [2] - [11] .
Others forms of parallel implementations were proposed using mulprocessing and/or multithreading as in [12] - [14] . In Boost1, optimized versions of Dijkstra’s algorithm are proposed for various representations of graphs. BGL2 library [15] [16] , based on incidence graph representation, uses multithreading concept to paral- lelize applications.
Edmond et al. [17] propose parallel implementation of Dijkstra’s algorithm, consisting to three super steps. In each super-step, processors communicate to select node u with minimum weight m, m = mind(u) u Î list of unvisited nodes. In this approach more parallelism is obtained when all nodes satisfying d(u) > m are removed and their outgoing nodes are relaxed.
The “Eager” Dijkstra’s Algorithm [18] uses a relatively easy heuristic to determine the nodes to relax during a super-step. A constant factor is set: l = min {weight(e)/e Î E, list of edges} and in each superstep the processors remove all node u such that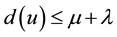
, ordered by ascending values of d(u) (u = mind(u) u Î list of unvisited nodes). In this method, parallelization degree depends on l.
Crauser et al.’s algorithm [12] uses more accurate heuristic to increase the number of nodes to remove every super-step without reintroducing nodes already deleted: the criterion for outgoing nodes calculates a threshold based on the weights of the outgoing edges in the graph: L = min{d(u)+ weight(u,w): u is queued and (u,w) Î E}. The criterion for entering nodes calculates a threshold based on the nodes entering:
if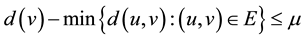 
(where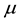 
is the global minimum of nodes contained in the waiting list). The two criteria can be combined. Nodes satisfying one of the two criteria are removed. This method needs 
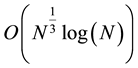time with high probability.
Okuyama et al. [9] propose a Dijkstra implementation on GPU with 3.4 to 15 times faster than the prior method. They use on-chip memory, to eliminate approximately 20% of data loads from off-chip memory.
In their work, Ortega-Arranz et al. [10] significantly speed up the computation of the SSSP from 13× to 220× with respect to the CPU version and a performance gain of up to 17% with respect to the GPU-Martin’s algorithm.
Our works focus on Dijkstra’s algorithm on graph represented in adjacency matrix. We use two platforms and two parallel versions of the algorithm. The paper is organized as follows. In Section 2, it is an overview of the Dijkstra algoritm, graph representation and CUDA3 programming model. Section 3 presents the approach used and experimental materials. Section 4 presents the results of the implementation and Section 5 presents conclusion and future work.
2. Background
Algorithm’s category concerned
This study concerns algorithms with iterative main loop (while, for, etc.), inside which there is at less a join operation. Join operation can be done on CPU or on GPU as a reduction. So operations can be shared between CPU and GPU. The general execution form of those algorithms is illustred in Figure 1. Dijkstra’s algorithm on the shortest path and Ford-Fulkerson’s algorithm are exemples of this class. The reduction operation in Dijkstra algorithm is when global minimum is researched. For the rest, we will consider Dijkstra’s algorithm on the shortest path.
![]()
Figure 1. General form of concerned algorithms.
2.1. Presentation of the Algorithm
As noted in [1] , Dijkstra’s single-source shortest paths algorithm is used to determine the shortest path between two vertices of a connected graph weighted, directed or not. Each edge of the graph has a positive or zero weight. This algorithm is usually used to solve optimization problems.
Principle of the algorithm
From the start vertex, Dijkstra’s algorithm constructs a subgraph consisting of vertices to visit in order to reach the top destination. The weight of the shortest path connecting the start vertex to finish destination is equal to the sum of the weights of the edges followed. In simple, the algorithm can be summarized in three steps:
Fix the starting vertex and assign zero distance (0); adjacent vertices to it have distances equal to the weight of the arc that connects them to the starting vertex. The other vertices have infinite distances (+¥), meaning that the exact distance is not determined. Then, the minimum distance of adjacent vertices is selected and the vertex concerned is added to the list of visited vertices.
Update the distances of the vertices adjacent to the visited node. If the new calculated distance is less than which already exists, it replaces the old value.
Selecting again the vertex with the minimum distance and insert it to the list of visited vertices. This process continues from the last vertex added until exhaustion of all vertices or when the destination is reached.
Figure 2 shows flowchart of Dijkstra’s algorithm.
2.2. Example of Using Dijkstra’s Algorithm
In Figure 3, nodes represent cities identified by a letter and numbers on edges indicate the distances. We seek the shortest road connecting the cities E and S. Table 1 provides the shortest path from E to S with 6 as weight. It is composed by E-A-C-S.
2.3. Graph Representaion
A graph G consists of a finite set of vertices (or nodes) denoted by V and a subset E of V ´ V whose elements are
called edges. We note G = (V, E). Similarly, we note the number of vertices N in graph G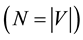 
and M the number of edges of the graph
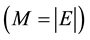. For the graphs we deal with in this paper, we assume that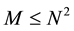 
which means that between two vertices u and v, there are only two possible oriented edges: u ® v or v ® u. There are many possibilities to represent shortest graphs [19] . Two structures are in the list of most widespread:
Adjacency list
Each vertex contains a list of its adjacent vertices. In this representation the space occupied by the graph is proportional to the number of edges of the graph but an edge occupies a relatively large space.
Adjacency matrix.
Graph is represented in a square matrix of order N, indexed by row and column vertices. For two vertices u and v, the input (u,v) of the matrix gives the weight of the edge from u to v if it exists. When there's no edge from u to v, the input (u,v) equal to +¥.
Representation used
In this paper, we use adjacency matrix representation of graph because of its usefull. In addition to the adjacency matrix, the algorithm uses three vectors of size N:
1) D contains optimum weight from start node (S) to another node i. This weight is stored in D[i].
2) M indicates if a vertex is visited or not. When a vertex is visited M[i] equal to 1 else 0.
![]()
Figure 2. Operational flowchart of Dijkstra’s algorithm.
![]()
Figure 3. A graph exemple: nodes represent cities, numbers are distances between them.
![]()
Table 1. Steps of Dijkstra’s algorithm applied on graph in Figure 3.
3) P contains the previous vertex of each vertex (when possible) during the execution of the algorithm.
For graph in Figure 3, N = 6. At the initialization step, we obtain adjacency matrix G, weights vector D, status vector M and predecessors vector P as given in Table 2.
2.4. GP-GPU’s Computation
In the past, GPU is destined only for video games because of its graphics processors. Since few years, GPU is also used in massively parallel computing. In fact, GPU’s properties provide opportunities for parallel compu- ting. New interest of using GPU for parallel computing is due to their very low costs for very high performance.
2.4.1. CUDA Programming
From 2006, NVIDIA released a DirectX-based on GPU with CUDA. CUDA architecture includes components for general treatments on GPU. CUDA programming consists to reprogram C code with CUDA extension as we do in OpenMP or MPI for instance. CUDA needs a graphics card with a NVIDIA Fermi processor, GForce8XXX/Tesla/Quadro, and CUDA C compiler, NVCC [20] - [25] .
2.4.2. Memory and Threads Organization on GPU
As shown in Figure 4, thread is the basic level of computation on GPU. Threads executing concurrentially are grouped into block. Blocks are grouped in the grid. Each thread has its own local memory and its own working registers. Shared memory is dedicated to each block and is only accessible to threads of the same block. In addition each block has a private memory for saving block's general elements. At last, a global memory is dedicated for the whole GPU. It is used by the grid and provides communication between the GPU (device) and the CPU(host) [20] .
2.4.3. Grid, Block and Threads: Disposition
Before launching a kernel4, we must define the grid on which it will be executed [21] [22] . A grid is a set of blocks arranged in one, two or three dimensions. A block is a multiprocessing unit (cores). One must specify the number of threads contained in a block and the number of blocks constituting the grid. GridDim variable is used to set the number of blocks. Block can be arranged in one, two or three dimensions. The variable blockIdx.x component indicates the first size, blockIdx.y provides the second dimension and blockIdx.z returns the third dimension. Each block has an identifier representing its number, ranging from 0 to gridDim.x-1.
As the block, the thread is organized in three ways:
in table of single dimension. Threads are identified using a single variable x. The number of threads per block is given by block-Dim.x.
![]()
Figure 4. Principle of CUDA architecture [23] .
in two-dimensional array. Threads are determined by two variables (x, y).
or in three-dimensional array. The identifier of each thread is a function of three variables (x, y, z).
Thus, blocks and threads are structured in Dim3 a special structure with three elements (x, y, z) used particularly in CUDA. When one of these values is not set, system assigns the default value 1. For instance Dim3 grid(256) corresponds to a grid size 256 × 1 × 1 and Dim3 block(64, 64) corresponds a block of size 64 × 64 × 1 (Figure 5).
3. Proposed Approach and Materials
To make parallel calculations performed on the matrix’s graph for determining the shortest path, we proceed in two steps as below:
1) transformation of the graph in to a matrix-vector-linear. Indices of elements of this vector will be used to designate threads identifier.
2) allocation of enough computation units, such that each element of the vector (matrix-graph) is managed by a calculation unit.
3.1. Transformation of the Graph Matrix
Graph G is represented in adjacency matrix. This matrix is carried out using an array: an edge of the graph connecting vertices(u, v) is represented by element indiced ![]()
of an array of size N2. Thus, for instance the matrix graph shown in Table 3(a) is transformed as in Table 4.
![]()
Figure 5. Structure of the grid computing.
![]()
Table 4.Representation of the graph in a vector-matrix of N2 elements.
3.2. Distribution of Computations between Units
Parallelizing calculations requires a thorough examination of the dependencies between them [25] . Dijkstra’s algorithm on the shortest path is structured in three (3) loops for:
A main loop which cannot be parallelized. This loop treat the vertices one by one ordered ascending weight from the source vertex to the destination vertex.
The two other inner loops can be parallelized.
The first inner loop selects among all the adjacents vertices not marked, the one with the minimum weight. At this step, the set of vertices to be processed is divided into groups. Each group is processed by a computer unit (block). When calculations are finished, each unit returns its relative minimum vertex. At last the global minimum is selected.
This processing is performed on the GPU. It consists to a reduction operation where the minimums are compared gradually to extract the global minimum. Its code is given in Algorithm 1.
The second inner loop updates the weights of vertices. It is parallelized: each computer unit processes a group of vertices for updating, as described in Algorithm 2.
In Algorithm 1, 2 and 3, we assume:
G: a graph;
M: status vector indicating if a node is visited or not;
Ind: array of vertices numbers;
k: integer;
gindice : array of vertices numbers on the GP-GPU:
N: size of vector (number of vertices in the graph);
u: node of G;
D: vector of provisories weights to the start node;
block_size: number of threads in a block;
num_blocks: number of blocks contained in the grid;
GPU1, GPU2: kernels (Figure 6).
![]()
![]()
(a) (b)
Figure 6. Overall occupancy of the computing units: global minimum using Algorithm 1 and the update of edges weights is shared between computing units as described in Algorithm 2.
![]()
![]()
3.3. Material and Datas
Our research took place in two stages. During the first stage, we used platform 2 and experienced the two parallel implementations of Dijkstra’s algorithm: one based on the CPU memory (zero-copy memory) and the other one uses GPU memory (with copying data). Unfortunately, this platform does not allowed us to test large graphs (containing more than 16,384 vertices) because of its limited power. That is why, experiments were re- peated on platform 1 and graphs containing 65,536 vertices were tested. So, results of platform 1 have con- firmed those obtained on platform 2, for large graphs.
Characteristics of experimental platforms are as follow:
Platform 1:
The CPU is an Intel CoreTM2 Duo 3Ghz x64, operating at 1.333Gz and 4GiB memory. The nvidia Geforce GTX 570 HD has 480 cores, 1280 Mo for global memory, 48 Mo of shared memory, 64 Mo of constant memory. The compilator used is gcc vs 4.4.6 under Ubuntu 11.10, x86_64.
Platform 2:
The CPU is an Pentium Dual-Core CPU E5500 operating at 2.80Ghz and 2.80 Ghz with 3 GiB of memory. The nvidia GeForce GTX 670 has 1344 cores, 2048 Mo of global memory, 48 Mo of shared memory and 64 Mo of constant memory. The compilator used is gcc vs 4.5.2 under Ubuntu 11.04, natty i686_64.
Code used
The prior Dijkstra’s algorithm used is based on adjacency matrix. It was modified to take under consideration the data structure and platforms. On both platforms codes were written in c++ with Nvidia’s CUDA language extensions for the GPU.
Data source
Graphs used in our tests have different sources:
-downloaded from the 9th DIMACS Implementation Challenge and US Census Bureau website [26] [27] ;
-obtained by running:
GTgraph , a random graph generator program type (n, m) [28] ;
GTgraph with RMAT type using a probability for the production of graphs;
and RandomGraph.
Graph number of vertices are of form![]()
, where x is an integer, because we use a reduction function on GPU [24] .
4. Results and Modeling
4.1. Results
Table 5 and Table 6 provide a summary of the realized measurements. It is noted that on platform1 the prior version of the algorithm is accelerated 3 to 10 times for algorithm version with copy and 4 to 30 times for version with zero-copy. On platform 2, version with copy processing perform 1.5 to 9 times and version without copy 3 to 18 times.
Figure 7 and Figure 8 show the time’s variation of the experiment results. In Figure 9 and Figure 10, accelerations of the two implementations on the two platforms are presented. On these figures plots in red color show the relative acceleration obtained between with-copy version and zero-copy version.
![]()
![]()
Figure 7. Performance on platform1 for various size of graphs.
![]()
Table 5. Results of experiments realized on the platform 1.
![]()
Figure 9. Variation of the acceleration on the platform 1 according to the size of the graph.
![]()
Figure 10. Variation of the acceleration on the platform 2 (Lami), according to the size of the graph.
![]()
Table 6. Results of experiments realized on the platform 2 (Lami, Ouagadougou, Burkina).
The two platforms present a similarity between the curves of data: performance for implementation with zero-copy memory is better than the implementation with data copy. However, copying data’s time constitute an important factor which reduce global algorithm’s performance.
Thanks: experiences of platform1 were done on the machine IBM Power 6, at Labsticc of Université de Bretagne-Sud (UBS), Lorient-France.
Remark: On platform 2, we have been limited in trying to go beyond this size of graph due to our calculation capabilities. All measures were done more than 20 times and averages were calculated.
4.2. Mathematical Modeling of the GPU’s Time
In a calculation on GPU, program main starts running on CPU. GPU begins running when a kernel is en- countered. So, the begining of a kernel program indicates that processing control is to GPU, and at its end CPU takes control. Datas treated by GPU can be either on GPU memory or on CPU memory if the GPU has capabilities for using CudaHostAlloc(), a cuda function to map CPU memory for GPU.
We assume:
N: number of vertices in the graph;
α: kernel initialization time;
Te: execution time of a single iteration;
λ: memory bandwidth of the GPU.
CPU’s execution time: The theoretical execution time of the Dijkstra’s algorithm calculations on a sequential machine is given in (1), it is order of![]()
.
![]()
(1)
Implementation with zero-copy’s execution time: The theoretical time to compute the Dijkstra’s algorithm on GPU with zero-copy is given in expression (2). So, ![]()
, where lb()5 is the binary logarithm (or logarithm on base 2).
![]()
(2)
Thus, the theoretical acceleration achieved on GPU without copying memory is order of![]()
.
Implementation with copying data’s execution time: Solution with copying data implies to take into account the time used while doing copy. The theorical quantity of datas copied are estimated as follow:
At the begening of the computation we have to copy, weights vector (N elements), marked vector (N elements), and the matrix-graph (![]()
elements).
While running the loop main, we have to copy, the marked vector from CPU to GPU, the weights vector from device to device, and the marked vector (second time) from CPU to GPU.
At the end of the loop, we have to copy marked vector and weights vector. Expression (3) represents memory quantity to be copied during algorithm execution;
![]()
(3)
Thus, the supplementary time due to copies is![]()
, and can not be ignored if![]()
.
Remark: Note that to speed up the calculations, parameters block_size, num_blocks in algorithms 9 were set to suitable values for the sizes of graphs we handle. So, we conclude that it is suitable to use CPU memory (zero-copy) for algorithms with main loop containing a reduction operation (many copying data). However, memory zero-copy impacts also CPU performance because since it uses a part of CPU memory.
5. Conclusions
In the present work, we study the impact of copying data when executing algorithms on GPU. In particular, we exam class of algorithms which runs a part time on GPU and another part time on CPU copying data and inter- mediates results. The computation of Dijkstra’s algorithm on the shortest path for graphs represented in adjacency matrix is took as an example. Two implementations are examined: one uses memory zero-copy (so the memory is located on CPU) and another one uses copying data on GPU. Performances are analysed on two differents machines with external GPU. The results obtained show the interest of our study. Computations are performed 2 times in solution with zero-copy compared to solution with copying data.
So the copying data’s time is equal to or greater than the computational’s time. This study shows an important impact of copying data on the global performance of an algorithm in GPU computing.
The new challenge for GPU’s manufacturers is how to reduce this impact.
In our future work prospects, we plan to:
redo this experiment on internal GPU. In this architecture, CPU and GPU have memory at the same space.
extend to Dijkstra’s algorithm for graphs represented in adjascency list. This graph’s representation provides better memory use and can handle very large graphs.
extend to the algorithms of Ford-Fulkerson and Edmond-Karp on the cut of graphs.
NOTES
1Boost is a set of free software libraries written in C++ to replace the C++ Standard Library.
2Boost Graph Library.
3Compute Unified Device Architecture.
![]()
4Program running on GPU. In its description, it appears as a process preceded by the keyword “__global__”.
![]()
5Notation recommended by ISO. lb(x) = ln(x)*lb(e) and lb(e)' 1,442695041.