Inertial Manifolds for 2D Generalized MHD System

Zhaoqin Yuan, Liang Guo, Guoguang Lin^*

Department of Mathematics, Yunnan University, Kunming, China.

DOI: 10.4236/ijmnta.2015.43014                

Abstract

In this paper, we prove the existence of inertial manifolds for 2D generalized MHD system under the spectral gap condition.

Keywords

MHD System, Spectral Gap, Inertial Manifolds

1. Introduction

In [1] , Yuan, Guo and Lin prove the existence of global attractors and dimension estimation of a 2D genera- lized magnetohydrodynamic (MHD) system:

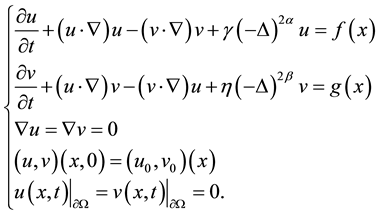(1.1)

where u is the fluid velocity field, v is the magnetic field, 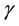is the constant kinematic viscosity and 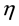is constant magnetic diffusivity. 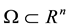is a bounded domain with a sufficiently smooth boundary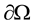,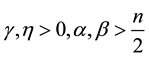. More results about inertial manifolds can be founded in [2] - [11] .

In this paper, we consider the following 2D generalized MHD system:

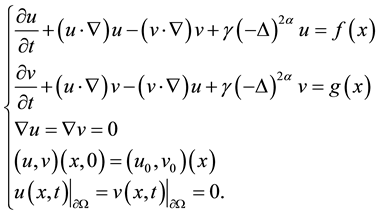(1.2)

where u is the fluid velocity field, v is the magnetic field, 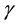is the constant kinematic viscosity and 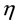is the constant magnetic diffusivity. 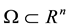is a bounded domain with a sufficiently smooth boundary, .

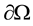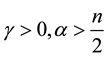This paper is organized as follows. In Section 2, we introduce basic concepts concerning inertial manifolds. In Section 3, we obtain the existence of the inertial manifolds.

2. Preliminaries

We rewrite the problem (1.2) as a first order differential equation, the problem (1.2) is equivalent to:

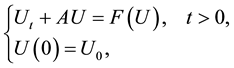(2.1)

where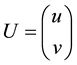, , 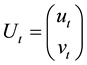and

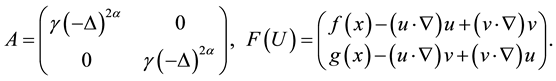
Let H is a Banach space, , is norm of H, is inner product of H, ;, for any solution of the problem (2.1), , is norm of.

Definition 2.1. Suppose denote the semi-group of solutions to the problem (2.l) in, subset M is an inertial manifolds of the problem (2.l), that is M satisfying the following properties:

1. M is a finite dimensional Lipshitz manifold;

2. M is positively invariant under, that is, for all;

3. M is attracts every trajectory exponentially, i.e., for every,

We now recall some notions. Let is a closed linear operator on satisfying the following Standing Hypothesis 2.2.

Standing Hypothesis 2.2. We suppose that is a positive definite, self-adjoint operator with a discrete spectrum, compacts in. Assume is the orthonormal basis in consisting of the corresponding eigenfunctions of the operator. Say

(2.2)

each with finite multiplicity and.

Let now and be two successive and different eigenvalues with, let further P be the orthogonal projection onto the first N eigenvectors of the operator.

Let the bound absorbing set, we define a smooth truncated function by setting is defined as

(2.3)

Suppose that the problem (2.1) is equivalent to the following preliminary equation:

(2.4)

Denote by is the orthogonal projection of H onto, and. Set, then Equation (2.4) is equivalent to

(2.5)

(2.6)

Lemma 2.3. Defined by of the problem (2.1) on the bounded set of is a Lipschitz function, for every, there exist a constant such that

(2.7)

where.

Proof. Assume, and let, use the fact that and using Poincare inequality, we have

(2.8)

where, so we can get

(2.9)

Lemma 2.3 is proved.

Lemma 2.4. Let be fixed, for any and all, there exist such that

(2.10)

otherwise, there exist constants and are dependent on such that

(2.11)

and

(2.12)

for all

Proof. Let with initial values respectively, are two different solutions of the problem (2.1), we have the fact that,. Put, so we obtain that

(2.13)

Putting

(2.14)

For, taking the derivative of Equation (2.14) with respect to t,we have

(2.15)

From Equation (2.13) and Equation (2.15), we have

(2.16)

We notice that Equation (2.14)

so we have

(2.17)

By Equation (2.16) and Equation (2.17), and use the Cauchy-Schwarz inequality, we obtain

(2.18)

Then using Lemma 2.3,we have

For, integrating the above inequality over, we obtain

(2.19)

where is given as in Lemma 2.3.

By multiplying (2.13) by, using Cauchy-Schwarz inequality and Lemma 2.3, we have

(2.20)

Using Holder inequality, from Equation (2.20) we have

(2.21)

In Equation (2.19) setting, we obtain

(2.22)

where

(2.23)

By Equation (2.21) and Equation (2.22), we have

(2.24)

Integrating Equation (2.24) between 0 and, we obtain

(2.25)

To complete the proof of Lemma 2.4, we consider the following two cases,

(2.26)

and

(2.27)

We only consider Equation (2.26), in this case,

(2.28)

where is N + 1 eigenvector of the operator. By Equation (2.25) and Equation (2.28), we obtain

(2.29)

since, in Equation (2.29) setting, which proves Equation (2.11), where and. Using again Equation (2.20), we have

then we obtain

(2.30)

Integrating Equation (2.30) between 0 and, which proves Equation (2.12). Lemma 2.4 is proved.

3. Inertial Manifolds

In this section we will prove the existence of the inertial manifolds for solutions to the problem (2.1). We suppose that satisfies Standing Hypothesis 2.2 and recall that P is the orthogonal projection onto the first N orthonormal eigenvectors of.

Let constants be fixed, we define and denote the collection of all functions satisfies

(3.1)

Note that

(3.2)

is the distance of. So is completely space.

For every and the initial data, the initial value problem

(3.3)

possesses a unique solution.

(3.4)

where and the unique solution in Equation (3.4) is a successive bounded mapping acts from into. Particularly, the function

(3.5)

by, note that, we have

(3.6)

We need to prove the following two conclusions:

1. For and are sufficiently large, is a contraction.

2. is a unique fixed point in T, is a inertial manifold of 2D generalized MHD system.

So we give the following Lemmas.

Lemma 3.1. Let, so we have

(3.7)

Proof. The proof is similar to Temam [3] .

Lemma 3.2. Let, for, there exists constant such that

(3.8)

and

(3.9)

Proof. For any and, we denote, using Lemma 2.3 and see ([3] , Chapter 8: Lemma 2.1 and Lemma 2.2), we derive that there exists constant such that

(3.10)

and

(3.11)

which proves Equation (3.8). We now prove Equation (3.9), by the definition of, we have

(3.12)

And we have

(3.13)

Substituting Equation (3.13) into Equation (3.11) we obtain Equation (3.9). Lemma 3.2 is proved.

Lemma 3.3. Let, one has and where for is sufficiently large one has.

Proof. Let, according to the definition of, we have, from Equation (3.6) and Equation (3.10), we have

(3.14)

Let and, suppose that and

So we obtain

(3.15)

Further more, for, we have

(3.16)

Setting in, then substituting into Equation (3.15) and Equation (3.16), and from Equation (3.14) we can derive that

(3.17)

Lemma 3.3 is proved.

Lemma 3.4. Let

(3.18)

so for every, one has

(3.19)

here

(3.20)

(3.21)

(3.22)

Proof. For any given, let are the solutions of the following initial value problem,

(3.23)

and

(3.24)

here Suppose that, so we have

(3.25)

Multiplying the first equation in Equation (3.25) by, using Equation (3.9) in Lemma 3.2, we obtain

(3.26)

So we have

(3.27)

For, from Equation (3.27) we have

(3.28)

By Lemma 2.3, to do the following estimate,using Equation (3.11) and Equation (3.28) we obtain

(3.29)

here. From Equation (3.15), we have

(3.30)

here.

Hence,

(3.31)

Then from Equation (3.15) we have

(3.32)

Combining Equation (3.31) and Equation (3.32), we obtain

(3.33)

Substituting Equation (3.33) into Equation (3.29), we obtain

Lemma 3.4 is proved.

Lemma 3.5. Let is defined as in Lemma 3.4, for all,

(3.34)

here is defined by Equation (3.20), is defined by Equation (3.2).

Proof. Let and let is the solution of the initial value problem (3.25), then by the same way as in Lemma 3.2 we can prove that

(3.35)

From the first inequality of Equation (3.26) and the following estimate, we have

then from the last inequality of Equation (3.35), we obtain

(3.36)

From Equation (3.36), we have

(3.37)

Due to, integrating Equation (3.37) over, we have

(3.38)

From Equation (3.6), Equation (3.35) and Equation (3.38), we have

(3.39)

Then using Equation (3.16), Equation (3.33) and, we have

(3.40)

Lemma 3.5 is proved.

Lemma 3.6. Suppose that

(3.41)

(3.42)

we have and, where is defined as in Lemma 3.5,

(3.43)

Proof. From is equivalent to

(3.44)

where and are defined as in Lemma 3.4. To find a sufficient condition of Equation (3.44), suppose that Equation (3.44) hold, so we have

(3.45)

To make, if and only if it satisfies

(3.46)

(3.47)

Equation (3.46) is equivalent to

(3.48)

If Equation (3.48) is satisfied, so Equation (3.47) is equivalent to or is equivalent to

(3.49)

Suppose that Equation (3.41) is equivalent to

(3.50)

Hence,

(3.51)

Hence,

(3.52)

Therefore Equation (3.49) follows from Equation (3.52). From Equation (3.41) we conclude that, Equation (3.48) follows from Equation (3.41), Equation (3.46) follows from Equation (3.48), Equation (3.46) follows from Equation (3.49), and from Equation (3.46) and Equation (3.47) we have. The last we need to prove is, from Lemma 3.5, we obtain

(3.53)

we notice that. Lemma 3.6 is proved.

From Lemma 3.1 to Lemma 3.6,we can obtain the following conclusions.

Theorem 3.1. Suppose that is Lipschitz mapping space. satisfy Equation (3.1) and Equation (3.2), and is the unique solution of Equation (3.3) and Equation (3.4) for, respectively. Hence the transformation is a contraction, and exists a unique fixed point, is inertial manifolds of the problem (2.1).

Theorem 3.2. Suppose that is the mapping of, for any, there exists such that, for,

(3.54)

where, is defined as in Lemma 2.3.

Proof. Let with initial value, respectively, be two solutions of the problem (2.1). For any arbitrary and for, and use the fact there exists a constant

such that Equation (2.10) or Equation (2.11) is satisfied. From Equation (2.12), we have

(3.55)

Assume and for, therefore Equation (2.10) and Equation (2.11) can rewrite

(3.56)

(3.57)

Let is absorbing set, the orbital solution satisfies. Let such that

(3.58)

Substituting and into Equation (3.56) and Equation (3.57), we have

(3.59)

If Equation (3.56) is satisfied, assume, so we have the cone property

(3.60)

In a word, for, whenever By the properties of semigroups, for, we have

(3.61)

Theorem 3.2 is proved.

Supported

This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Yuan, Z.Q., Guo, L. and Lin, G.G. (2015) Global Attractors and Dimension Estimation of the 2D Generalized MHD System with Extra Force. Applied Mathematics, 6, 724-736. http://dx.doi.org/10.4236/am.2015.64068
[2]	Lin, G.G. (2009) An Inertial Manifold of the 2D Swift-Hohenberg Equation. Journal of Yunnan University, 31, 334-340.
[3]	Temam, R. (1988) Infinite Dimensional Dynamical Systems in Mechanics and Physics. Springer, New York. http://dx.doi.org/10.1007/978-1-4684-0313-8
[4]	Constantin, P., Foias, C., Nicolaenko, B. and Temam, R. (1989) Integral Manifolds and Inertial Manifolds for Dissipative Partial Differential Equations. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-3506-4
[5]	Lin, G.G. (2011) Nonlinear Evolution Equations. Yunnan University, Kunming.
[6]	Babin, A.V. and Vishik, M.I. (1992) Attractors of Evolution Equations. North-Holland, Amsterdam.
[7]	Chow, S.-N. and Lu, K. (1988) Invariant Manifolds for Flows in Banach Spaces. Journal of Differential Equations, 74, 285-317. http://dx.doi.org/10.1016/0022-0396(88)90007-1
[8]	Chueshov, I.D. (1992) Introduction to the Theory of Inertial Manifolds, (Lecture Notes). Kharkov Univ. Press, Kharkov (in Russian).
[9]	Chueshov, I.D. (1999) Introduction to the Theory of Infinite-Dimensional Dissipative Systems. Acta, Kharkov (in Russian) (English Translation, 2002, Acta, Kharkov).
[10]	Henry, D. (1981) Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Math. 840. Springer, Berlin-Heidelberg and New York.
[11]	Leung, A.W. (1989) Systems of Nonlinear Partial Differential Equations: Applications to Biology and Engineering. MIA, Kluwer, Boston.