Using Baseball Data as a Gentle Introduction to Teaching Linear Regression ()
1. Introduction
Teaching statistics to MBA students is a challenge. A part of the reason for this is that many different academic backgrounds comprise the class: liberal arts, engineering, social sciences, hard sciences, history, education and so on. With such a diverse group, learning statistics is harder for some students than others. Linear regression is no exception to this―while most students can easily understand the concept of a slope and intercept, the statistical significance of the slope and intercept, and predictive ability of the model, can be more challenging, particularly for those students who struggle with the basics of hypothesis testing in earlier class sessions.
This dilemma has been noted over the years, and because of this, a simple example has been developed for the Working Professional MBA Classes at Wake Forest University’s School of Business that has eased the introduction of linear regression to the students. Instead of a typical example exploring the relationship between price and demand for some generic good, a baseball example has been used with consistent success.
The idea for this example came from an earlier edition of the classic text book by Albright, Winston and Zappe (2011) , where a scatter plot was shown to illustrate the relationship between the annual payroll of a Major League Baseball team and the team’s winning percentage for that same year. Other studies have investigated salary to individual performance (Watnik, 1988; Hoaglin & Velleman, 1995) , but the author is not aware of any continuous exploration of the relationship between team success and team payroll. Over the years, this simple example has been developed to study the relationship between payroll and winning percentage in terms of the statistical significance of the slope and the model’s predictive ability. The model has been further developed to include multiple predictor variables so that the model’s predictive ability is maximized while simultaneously maintaining a parsimonious model.
2. Does a Baseball Team’s Payroll Result in Success?
The short answer to the above question is “not really,” but this question is the “teaser” for the exercise. A discussion is then encouraged in the classroom about the relationship between a baseball team’s payroll and their winning percentage. The following comments from the students are typical:
The New York Yankees typically have the highest payroll in the game, but sometimes they’re good, sometimes they’re not so good.
Teams like the Pittsburgh Pirates, Tampa Bay Rays and Oakland Athletics usually perform well with small payrolls.
Big city teams usually have a large payroll, regardless of whether or not they are successful. Teams in New York, Chicago and Los Angeles are what the students consider “big city” teams.
All of the above points are well taken. Data are then presented to them which show the team’s payroll and winning percentage for the most recently completed regular season. For the 2013 regular season, the data are as follows:
From inspection of Table 1, the points made by the students above are essentially supported by the data. Converting the data into a scatter plot, along with the “best-fit” regression line, we have what is shown in Figure 1.
The points made by the students are further supported by the scatter plot. In essence, any team “above” the regression line outperforms their payroll, and any team “under” the regression line underachieves according to their payroll.
At this point, the statistical inference portion of the exercise is performed. The slope term has a t-statistic of 1.73, while the associated p-value is 0.0953. This does not indicate a strong relationship between payroll and winning percentage. Only at α = 0.10, the most liberal level of significance commonly used, can one reject the null hypothesis of a meaningless slope. In essence, then, the relationship between payroll and winning percentage is dubious at best. This finding is quite surprising to the students. In fact, there are always students at this point in the exercise who question the New York Yankees high-payroll strategy.
To further dampen this analysis, the R2 term is discussed, showing that only 9.62% of the variation in a team’s winning percentage can be explained by their payroll. The lesson learned here is that there is a weak relationship between payroll and winning percentage, and our ability to use this model as a predictive tool is non-existent.
The next order of business is to inform the students that there may be other ways to “explain” winning percentage other than the team’s payroll.
3. Multiple Linear Regression as a Tool to Explain Winning Percentage
To improve the ability to “explain” the variation in the team’s winning percentage, the concept of multiple linear regression is introduced, where it is mentioned that adding new predictor variables can help to increase the R2 term. That is, it is mentioned that one can do a better job of explaining the variation in the team’s winning percentage. It is also emphasized that we must be frugal in adding predictor variables, as many predictor variables in a single model can make the model difficult to interpret. In the context of our baseball example, Payroll is removed and five new predictor variables are introduced. Table 2 shows the new data set.
The five new predictor variables are as follows:
ERA: Earned Run Average. The number of earned runs forfeited per nine innings pitched during the 2013 season.
BB: Bases on balls. The number of times a player was “walked” during the 2013 season.
RBI: the number of runs batted in during the 2013 season.
Slug: The slugging percentage of a team during the 2013 season. Total bases divided by plate appearances.
![]()
Figure 1. Payroll and winning % for 2013 season.
WS Manager: the number of World Series titles won by the team’s manager at the beginning of the 2013 season.
The five new predictor variables are used in a multiple linear regression model with winning percentage as the response variable. Of course, the R2 term increases dramatically from the simple linear regression. However, the model is cumbersome due to the inclusion of non-significant predictor variables and multicollinearity―correlation between predictor variables, hindering our ability to properly interpret the significance of individual predictor variables.
After removing the predictor variables due to insignificance, and removing others to be explained by remaining variables due to multicollinearity, the following model is obtained:
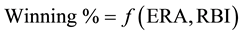
Including payroll, six total predictor variables were candidates to explain winning percentage, and only two are needed to explain winning percentage: ERA and RBI. The slope terms show the following statistical properties (Table 3):
This model results in an R2 term of 0.8830% - 88.30% of the variation in winning percentage is explained by ERA and RBI.
The astute students will usually note that the two remaining predictor variables make total sense. One is an offensive statistic―RBI is a measure of run-production, while the other is a defensive statistic―ERA is a pitcher’s ability to prevent the opposition from scoring runs.
The cynical student will also note that the outcome from the exercise was obvious from the start―teams that score lots of runs and prevent the other team from scoring runs will be successful. This point is very well taken, and cannot be refuted. However, it is pointed out to the cynical student that several other, presumably important, variables were similarly explored and eliminated because of their lack of ability to explain winning percentage. These cynical students then agree that exploring other variables (such as payroll) was in fact worth doing.
At the conclusion of this exercise, it is also mentioned that having only two remaining predictor variables (ERA and RBI) is a good thing, as a parsimonious model is much easier to articulate as opposed to a more complicated model.
4. Conclusion and Effectiveness of Exercise
The example described has been used for about six years now. For AACSB re-accreditation purposes, learning objectives are monitored for each topic covered in quantitative methods. For each exam administered, several are randomly sampled, and for each, exam problems reflecting basic course concepts are graded for how well the student performs on the selected problems. While the administration is uncomfortable in sharing specific statistics, linear regression has always shown that learning objectives have been attained, and since the introduction of the baseball example, the attainment of these learning objectives has further improved.
Additionally, a survey was given to former students who were exposed to the baseball example. Three hundred students were invited to take the survey, and (133) of them responded, resulting in a response rate of 44%. The survey and resulting responses are included in the Appendix 1. Of particular note are a few following items. 47% of respondents feared quantitative methods, and 36% feared linear regression. 100% of the respondents found the baseball example a helpful introduction to linear regression, while 91% of the respondents found the baseball example preferable to a more traditional example of linear regression, which often involves supply and demand and the like.
Over the years, the example has evolved into a two-part exercise. The first week, the relationship between payroll and winning percentage is explored. Once it is established that this relationship is weak, other, more traditional linear regression examples are pursued. The second week, multiple linear regression is introduced, so that the student becomes aware of using multiple predictor variables to improve the R2 term, along with the pitfalls
![]()
Table 3. Statistics for multiple linear regression model.
of multicollinearity. At that point, the baseball example is revisited (with the additional predictor variables), where the intent is to maximize the R2 term with as few predictor variables as possible. Students are typically surprised that approximately 90% of the variation in a team’s winning percentage can be explained by just two predictor variables. 98% of the students surveyed found this particular transition from simple to multiple linear regression helpful.
The survey also gives the students the opportunity to discuss their thoughts on the baseball introduction to regression. A summary of some frequent comments are as follows:
The baseball example was a more understandable introduction to understanding the relationship between variables, as compared with more traditional examples shown in business school quantitative methods books. Students mentioned that they can better relate to the relationship between payroll and winning percentage as compared with something more esoteric.
The baseball example was a good way to better understand the difference between independent variables (payroll) vs. dependent variables (winning percentage).
Adding more independent variables, such as ERA and RBI is a good way to increase the predictive ability of the model.
The conversation is then brought to a close by mentioning sabermetrics, data-mining and the newer “analytics” tools currently used by sports teams to find patterns in data that can result in a competitive advantage (Lewis, 2003) .
Acknowledgements
The author would like to sincerely thank the Working Professional MBA students at Wake Forest University for their feedback on the use of this teaching approach. This paper would not have been possible without their survey participation.
Appendix
Appendix 1. Survey instrument used.