1. Introduction
Plenty of grain and oil reserves in each region are important for the protection of non-food consumer demand, regulating the supply and demand balance of domestic food, stabilizing grain prices, responding to major natural disasters or other emergencies, to protect the security and stability of society. Each year, after the harvest season, the national authorities will carry out the acquisition of grain and oil supplies, then according to the needs of each locality, make allocation of distribution, to ensure that each place has plenty of grain and oil reserves. Grain and oil materials need to be transported to the country, however, facing the complex road conditions and the different demand for grain and oil reserve materials of each different places, if we do not make an overall plan, it will cause an increase transport costs in the deployment, cause the shortage or excess supplies of local grain reserve, and affect the life of people and the security and stability of society. Therefore, under the premise of meeting the minimum needs of grain and oil of different areas, how to use the lowest transportation costs to convey the grain and oil materials to various reserve repository as much as possible is worthy of study, and in the case of an emergency situation, how to deploy the grain and oil to meet the emergency needs faster and better is worthy of study.
Currently, the research of the application of the combination of shortest path and minimum cost maximum flow theory in grain and oil deployment is also less. Existing literatures has done some related research about this issue but only for one aspect. Shortest path theory is one of the most widely used network theories, many problems can be optimized by using this theory. It refers to the known network, seeking one way, of which the arc weight is minimum among all the ways from a specified node vi to another node vj [1] . In the study of the shortest path problem, [2] studied the shortest path problem in road transport network, and converted the optimization problem of choices to the shortest path problem, then solved the problem. [3] studied the application of the shortest path problem in tourist route optimization and obtained the shortest path from any view spot to another view spot, and as well as the shortest path problem about the two view spot of the way must be given. [4] proposed a solution procedure for the elementary shortest path problem with resource constraints, presented computational experiments of the algorithm for our specific problem and embedded in a column generation scheme for the classical vehicle routing problem with time windows. [5] tried to find an answer to the question of which shortest path algorithm for the one-to-one shortest path problem ran fastest on a large real-road network and solved the key problem of the computation of shortest paths between different locations on a road network, which appeared in many applications. [6] considered the variant of the shortest path problem in which a given set of paths was forbidden to occur as a subpath in an optimal path, established that the most-efficient algorithm for its solution, a dynamic programming algorithm, had polynomial time complexity, and showed that this algorithm could be extended, without increasing its time complexity, to handle non elementary forbidden paths. [7] investigated the time-dependent reliable shortest path problem, which was commonly encountered in congested urban road networks. Two variants of time-dependent reliable shortest path problem are considered in this study, and the proposed solution algorithms given in this study have potential applications in both advanced traveler information systems and stochastic dynamic traffic assignment models. In the study of the minimum cost maximum flow problem, [8] studied the application of the minimum cost maximum flow algorithm in path planning, and found a method to solve the complex problems of dynamic programming, which was generally difficult to be solved by traditional algorithm. [9] [10] studied the application of the minimum cost maximum flow model in the railroad freight and connecting cargo flights. The studies that both the methods are used for the deployment of grain and oil are less. [11] studied the resource scheduling scheme according to the optimal transport routes, the selection transport mode and the distribution of emergency supplies in order to deploy the most supplies from distribution center to urgent areas within the limited time. [12] [13] studied the optimization problem of oil distribution based on the minimum cost flow theory. [14] obtained an optimal route of a more realistic situation as to scheduling maximum flows at a minimum cost from a source to a destination. Several special cases of the problem were intensively studied in the literature and were solved by the proposed various techniques. [15] developed the fast algorithms for previously unstudied specially structured minimum cost flow problems that had applications in many areas, such as locomotive and airline scheduling, repositioning of empty rail freight cars, highway and river transportation, congestion pricing, shop loading, and production planning.
Previous research literature has laid a foundation to the further research about the related deployment of materials, but hasn’t yet combined the shortest path problem with the minimum cost maximum flow problem, then is applied to the study of the deployment of grain and oil, and hasn’t yet used the different models to analyze the different problems according to the different situations. This paper will establish the comprehensive mathematical model of the deployment of grain and oil supplies based on the researches of the shortest path problem and minimum cost maximum flow problem and will analyze and then present the deployment plans of grain and oil supplies in an emergency situation, in normal circumstance, and in special circumstance. This can provide some references more or less to the actual deployment of grain and oil supplies.
2. Application of the Shortest Path Theory in Grain and Oil Deployment
2.1. Emergency Logistics Problem Description
[16] hold the opinion that emergency logistics is a special logistics activity for the purpose of providing the emergency supplies for the unexpected natural disasters, public health emergencies and other unexpected emergencies, and for the purpose of pursuing the goal of the maximization of time benefits and the minimization of emergencies loss. Emergencies is the cause of emergency logistics, the natural disasters, the mistakes of decisions, the complex international environment, the protection of consumer rights, and the reasons from third parties is the main reason for emergency logistics demand generated [17] . Generally, emergency logistics have several typical features: sudden, uncertainty, uncertainty and weak economy [18] . Thus, emergency logistics is different from the general logistics, the requirements for timeliness of the emergency logistics is relatively high. We are generally unable to accurately estimate the burst duration, scope and intensity of the emergency events. It reflects an urgent word, when emergencies arise, if the logistics activities are carried out step by step, you will meet the demand for emergency logistics. So, the economic benefits of logistics will no longer be the central objective of logistics activities. Regardless, the sudden major natural disasters such as earthquakes, snowstorms or emergencies such as war, are bound to need a lot of emergency supplies, especially the grain and oil supplies. Therefore, the logistics systems are needed to play its role in the emergency response, and the benefit of logistics can be achieved through the logistics efficiency. And then, we can pursue the goal of the maximization of time benefits and the minimization of emergencies loss while meeting the needs of the emergency supplies of the emergency areas.
2.2. Strategy Analysis of Emergency Deployment
Sudden emergencies will cause a shortage of emergency supplies in the short term. In order to minimize the risks caused by the lack of emergency supplies, to ensure rapid deployment of emergency supplies becomes very important. Therefore, it is particularly important to deploy the most needed supplies at a certain number to emergency area within the shortest possible time.
Some researchers previously do a certain amount of research about deployment strategy in the emergency logistics.
[19] use the dynamic programming and integer programming to make the distribution strategy of emergency supplies after the earthquake, establish the distribution network between non-affected areas and emergency areas so as to deliver the much-needed emergency supplies to emergency areas in shortest time as soon as possible to improve the material distribution efficiency and reduce losses caused by disasters. [20] analyzed the features of the deployment of the emergency supplies of large-scale emergency events, designed and explained the whole process model of the deployment of the emergency supplies of large-scale emergency events from three stages: scheduling preparation, scheduling implementation and scheduling assessment. [21] researched the emergency supplies scheduling problem about more rescue points under constraints, constructed the emergency rescue model of the minimum number of rescue points under the premise of the earliest of emergency rescue time. [22] considered a variety of practical problems in the emergency areas, put forward a single objective path selection model for the propose of minimizing the time, and used the improved Dijkstra algorithm to solve the model. Then, on this basis, they constructed the complex multi-objective path selection model for the purpose of minimizing the time and minimizing the complex level of path, and solved the model with the ant colony algorithm.
In this paper, the shortest path theory will be used to make an appropriate deployment program of grain and oil in an emergency situation. The shortest path problem can be used to solve the problem that how the vehicle transport grain and oil supplies from source point to sink point at the minimum time, and it can be used to find the shortest path [23] . Typically, each province, in the deployment management of grain and oil, often adopt the regional distribution system to deploy the grain and oil from the deployment warehouse to the reserve station according to the division of administrative regions. Although it has a good feasibility, but in face of the emergency situations, the grain and oil supplies deployed from deployment warehouse to reserve station cannot fully meet the needs of emergency situations, and this will cause great loss. By using the minimum cost maximum flow theory, we can establish the transport corridors between the reserve station and reserve station, between the deployment warehouse and reserve station. Then, we can select the deployment warehouse owning grain and oil supplies to deploy grain and oil supplies to the reserve station lacking grain and oil supplies according to the shortest distance between points so as to respond quickly in an emergency event.
Then, we use Floyd algorithm to get the shortest distance between any two points. When the emergency event occurs, we can properly provide grain and oil supply from deployment warehouse or reserve station owning grain and oil to the emergency areas according to the grain and oil inventory of each reserve station and the shortest distance between each two points with the purpose of ensuring the sufficient grain and oil supply of the destination.
2.3. Model Establishment
1) Figure 1 shows the establishment of shortest network diagram of the grain and oil supplies deployment. Regard reserve station and other reserve station, reserve station and deployment warehouse as the nodes of the abstract network graph to establish an abstract network graph of connecting every point. Regard the time that the vehicle cost between any two connected points as the “distance” between two points. Regard vi, s as reserve station and deployment warehouse. Regard d as the weight of the abstract network graph. And, d represents the distance between two points. One-way arrow means the grain and oil supplies can only be deployed from one point to another point. Double-headed arrow means the grain and oil supplies can only be deployed between two points. The shortest network diagram of the grain and oil supplies deployment is as follows.
2) After obtaining the distance between two connected points, we write the corresponding distance matrix according to the shortest network diagram.

Among them, dij represents the distance between two points; ∞ represents infinite, means that there is no deployment of a reserve station to the deployment warehouse or a reserve station to a reserve station; 0 represents the deployment of a reserve station or deployment warehouse itself to itself.
2.4. Model Solution
Then, we can use the Floyd algorithm to solve the model.
The theory of Floyd algorithm:
Assuming that network weights matrix is D = (dij)n×n, it describes the length of the shortest path from vi to vj in the network. lij represents the weight of arc (vi, vj), means the distance from vi to vj. A represents the set of arc.
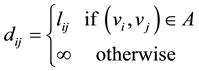
1) Only consider any two points vi and vj, other points are deleted except vi and vj, then, we get a subnet work D(0), which only contains vi and vj, denoted as:
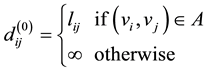
2) Add v1 and the arcs associated with vi, vj or v1 in D to D(0), we get D(1). If we denote 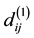 as the shortest length of the path from vi to vj in D(1), then:
as the shortest length of the path from vi to vj in D(1), then:

3) Add v2 and the arcs associated with vi, vj or v1v2 in D to D(0), we get D(2). If we denote 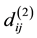 as the shortest length of the path from vi, to vj in D(2),then:
as the shortest length of the path from vi, to vj in D(2),then:

4) Recursively, Add n points to subnet work gradually, we get the shortest length of the shortest path finally from v1 to vj in D:
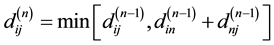
Then,  is the shortest length of the shortest path from vi to vj.
is the shortest length of the shortest path from vi to vj.
Thus, we obtain the shortest path between any two points that mean we get the shortest deployment time between any two points. Then, we can make appropriate deployment program of grain and oil in an emergency situations according to the shortest deployment time between any two points, and timely ensure that the demand of the areas for grain and oil.
3. Application of Minimum Cost Maximum Flow Theory in Grain and Oil Deployment
3.1. Problem Description
When there is no emergency situation, or after the acquisition of grain and oil, each region has some of the grain and oil reserves. In this condition, when we carry out the deployment of grain and oil, under the premise of meeting the minimum needs of grain and oil of different areas, how to use the lowest transport costs to convey the grain and oil materials to various reserve repositories as much as possible should be taken into consideration. In this case, exploring the application of minimum cost maximum flow theory in the deployment of grain and oil is more meaningful.
In this paper, the minimum cost maximum flow theory will be used to make appropriate deployment program of grain and oil in normal circumstances. The minimum cost maximum flow theory can be used to solve the problem that how the vehicle transport grain and oil supplies from source point to sink point at the minimum cost. This co-ordination arrangement will satisfy as much as possible to ensure the adequate supply of grain and oil of each areas in the steady state, while keeping the cost of the deployment process the minimum. And this can ensure social harmony and stability to a certain extent.
By minimum cost maximum flow theory, we can establish the transport corridors between the reserve station and reserve station, between the deployment warehouse and reserve station, we can establish the each maximum transport capacity of transport routes, and we can establish the unit transportation costs of each transport route.
Then, using the principles of the minimum cost and maximum flow to find the maximum flow from source point to sink point or from one point to another point, and we can get the best deployment plan.
3.2. Model Establishment
In the deployment process of grain and oil supplies, consideration is needed to ensure the minimum needs of grain and oil of different areas, and the lowest transport costs should be used to convey the grain and oil materials from deployment warehouse to reserve station as much as possible to realize the minimum total transportation costs, the largest volume of transport of grain and oil supplies in the whole process.
We assume that:
1) 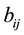 is the unit transportation costs of grain and oil supplies from the i deployment warehouse to the j reserve station.
is the unit transportation costs of grain and oil supplies from the i deployment warehouse to the j reserve station.
2) 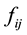 is the total amount of grain and oil supplies from the i deployment warehouse to the j reserve station.
is the total amount of grain and oil supplies from the i deployment warehouse to the j reserve station.
3) 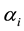 is the total amount of grain and oil supplies of the i deployment warehouse.
is the total amount of grain and oil supplies of the i deployment warehouse.
4) 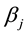 is the minimum required amount of grain and oil supplies of the j reserve station to ensure the needs.
is the minimum required amount of grain and oil supplies of the j reserve station to ensure the needs.
5) 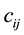 is the maximum traffic capacity of road from the i deployment warehouse to the j reserve station.
is the maximum traffic capacity of road from the i deployment warehouse to the j reserve station.
We regard the maximum number of deployment and the minimum total transportation costs as the objective function, regard the amount of grain and oil supplies of deployment warehouse, the as maximum traffic capacity of road, and the minimum required amount of grain and oil supplies of each reserve station as the constraints to establish the model. This model is as follows:
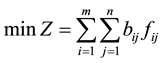
![]()
In the formula:
1) Constraint 1 represents the amount of grain and oil supplies deployed from the i deployment warehouse should not be more than the total amount of grain and oil supplies reserved in the deployment warehouse.
2) Constraint 2 represents the amount of grain and oil supplies deployed to the j reserve station should be more than the minimum required amount of grain and oil supplies of the j reserve station.
3) Constraint 3 represents the traffic capacity from the i deployment warehouse to the j reserve station should be within range of the maximum traffic capacity of road.
4) Constraint 4 represents the flow out of the middle points is equal to the flow into them.
5) Constraint 5 represents for source, the flow is not into it, but only flow out of it.
6) Constraint 6 represents for sink, the flow is not out of it, but only flow into it.
3.3. Model Solution
1) Because the solution of minimum cost and maximum network flow is in the condition of a single source point to a single sink point, so, when we deploy the grain and oil, involving a single deployment warehouse and multiple reserve stations, we can add a virtual point to the network graphics; when involving multiple deployment warehouses and multiple reserve stations, we can add a virtual source point and a virtual sink point to the network graphics.
Figure 2 shows the establishment of minimum cost and maximum flow network diagram of the grain and oil supplies deployment when there is a single deployment warehouse and multiple reserve stations. In this situation, regard s as the virtual source point. And, t represents the virtual deployment ware house. Regard A1, A2, A3, V1, V2, V3, V4, V5, V6 as the reserve station. We add t as a virtual point to the network graphics. And, t represents the virtual reserve station. The one-way arrow means the deployment of grain and oil supplies. And, the dij in (dij, cij) represents the unit transportation costs of grain and oil supplies, the cij in (dij, cij) represents the maximum traffic capacity of road from the i deployment warehouse to the j reserve station.
Figure 3 shows the establishment of minimum cost and maximum flow network diagram of the grain and oil
![]()
Figure 2. The minimum cost and maximum flow network diagram (including virtual sink point).
![]()
Figure 3. The minimum cost and maximum flow network diagram (including virtual source point and virtual sink point).
supplies deployment when there multiple deployment warehouses and multiple reserve stations. In this situation, we add s as the virtual source point, and s represents the deployment warehouse. Regard V1, V2, V3, V4, V5, V6 as the reserve station. We add t as a virtual point to the network graphics. And, t represents the virtual reserve station. The one-way arrow means the deployment of grain and oil supplies. And, the dij in (dij, cij) represents the unit transportation costs of grain and oil supplies, the cij in (dij, cij) represents the maximum traffic capacity of road from the i deployment warehouse to the j reserve station.
Further, the weight of arc from A1, A2, A3 to V1, V2, V3, V4, V5, V6 are respectiveas follows: (da1, ca1), (da2, ca2), (da3, ca3), (da4, ca4), (da5, ca5), (da6, ca6), (da7, ca7); (db1, cb1), (db2, cb2), (db3, cb3), (db4, cb4), (db5, cb5), (db6, cb6), (db7, cb7); (dc1, cc1), (dc2, cc2), (dc3, cc3), (dc4, cc4), (dc5, cc5), (dc6, cc6), (dc7, cc7).
2) Principles of the minimum cost and maximum flow
a) The minimum cost and maximum flow
For a network![]() , each arc
, each arc![]() ,
, ![]() is the capacity of the arc
is the capacity of the arc![]() , and
, and
![]() is a unit cost of flow through the arc
is a unit cost of flow through the arc![]() , abbreviated as
, abbreviated as![]() . Zé
. Zé
Then, the minimum cost and maximum flow: Seeking a maximum flow, so that the total cost of the flow:
![]()
is minimum.
b) Algorithm thought
If f is the minimum cost feasible flow among all feasible flow with the flow is![]() , and u is the minimum cost augmenting path among all augmenting path about f, then we can adjust f with the adjusting value
, and u is the minimum cost augmenting path among all augmenting path about f, then we can adjust f with the adjusting value ![]() along u, and we can get the feasible flow
along u, and we can get the feasible flow![]() . So,
. So, ![]() is the minimum cost feasible flow among all feasible flow with the flow is
is the minimum cost feasible flow among all feasible flow with the flow is![]() . When
. When ![]() is the maximal flow, then
is the maximal flow, then ![]() is the minimum cost and maximum flow we want to get.
is the minimum cost and maximum flow we want to get.
Therefore, if f is the minimum cost feasible flow with the flow is![]() , we must find the minimum cost augmenting path. At the moment, we can construct a weighted directed network graph
, we must find the minimum cost augmenting path. At the moment, we can construct a weighted directed network graph![]() , and the point of it is the same as the point of D The each arc and the weight
, and the point of it is the same as the point of D The each arc and the weight ![]() in the weighted directed network graph
in the weighted directed network graph ![]() can be can be classified according to the arc
can be can be classified according to the arc ![]() in the network D as fallows:
in the network D as fallows:
If![]() , and
, and ![]() (0 arc), then
(0 arc), then![]() , and
, and ![]()
If![]() , and
, and ![]() (saturated arc), then
(saturated arc), then![]() , and
, and ![]()
If![]() , and
, and![]() , then
, then![]() ,
, ![]() and
and![]() ,
, ![]()
Consequently, the problem that finding augmenting path of minimum cost about feasible flow is transformed into another problem that finding the shortest path from source point to sink point in the network diagram.
c) Algorithm steps
Firstly, assume that the initial feasible flow is![]() ,
, ![]()
Secondly, denote the minimum cost and maximum flow after k times adjustment as![]() , construct a network graph about cost as
, construct a network graph about cost as![]() .
.
Thirdly, find the shortest path from ![]() to
to ![]() in
in![]() . If there is no shortest path (the length of the shortest path is ∞), then
. If there is no shortest path (the length of the shortest path is ∞), then ![]() is the minimum cost and maximum flow; if there is a shortest path ,then the shortest path is the corresponding augmenting path
is the minimum cost and maximum flow; if there is a shortest path ,then the shortest path is the corresponding augmenting path ![]() in the network D. And, then transfer to step 4.
in the network D. And, then transfer to step 4.
Fourthly, according to the augmenting path![]() , adjust
, adjust ![]() with the he adjusting value
with the he adjusting value![]() :
:
![]()
![]()
Then, we get the feasible flow![]() , and go back to step 2.
, and go back to step 2.
Thus, we obtain the minimum cost and maximum flow from deployment warehouse to reserve station. Then, we can make appropriate deployment program of grain and oil in the normal circumstances to ensure adequate requirement of grain and oil of different areas at minimum cost.
4. Application of the Combination of Shortest Path and Minimum Cost Maximum Flow Theory in Grain and Oil Deployment
4.1. Circumstance Analysis
When the urgency of the emergency situation is in a lower level, if the whole deployment of grain and oil supplies only takes the time into consideration, and use the shortest path theory to solve the problem, because we only think that we deploy the grain and oil supplies in the shortest possible time in order to meet the demand of the area, without considering the transportation costs, so, the transportation cost will be very high. In order to better optimize the deployment plan, we need to take transportation costs into consideration, in this case, we can not only ensure the requirement of grain and oil supplies, but also ensures the reduction of the transportation costs as much as possible in the whole deployment process of grain and oil supplies. If the whole deployment of grain and oil supplies only use the minimum cost maximum flow theory to optimize, although we can transport grain and oil supplies to reserve station as much as possible at the lowest cost, however, we cannot guarantee the timeliness of supply, that means we cannot transport the grain and oil supplies to the desired place timely, and it will affect the demand for grain and oil supplies of the desired place. Consequently, in this case, how to make a better deployment program to convey the grain and oil supplies to the reserve station of destination as much as possible to ensure the emergency needs while reducing the whole transportation cost as much as possible is worth studying.
4.2. Strategic Planning
To begin with, we can use the shortest path theory to solve the problem of deploying the part of grain and oil supplies. Firstly, we can regard the time as the distance of the matrix, use the Floyd algorithm to find the shortest path in order to deploy the grain and oil supplies in the shortest time, and then we can regard the unit transportation costs as the distance of the matrix, use the Floyd algorithm to find the shortest path in order to deploy the grain and oil supplies with the minimum transportation costs to meet the requirement of grain and oil supplies in a certain period of time. Then, we can use the minimum cost maximum flow theory to solve the problem of deploying the other part of grain and oil supplies. By using this strategic plan, can we ensure that the overall cost of the whole deployment process is minimum.
1) Regard the time as the distance of the matrix, we can obtain the shortest path between any two points― the shortest time of deployment between any two points. Then, we can develop the deployment programs base on the shortest time of deployment to deploy the grain and oil supplies so as to meet the needs of grain and oil supplies of the destination timely to a certain period.
2) Regard the time as the distance of the matrix, we can obtain the shortest path between any two points― the minimum transportation costs of deployment between any two points. Then, we can develop the deployment programs base on the smallest unit transportation costs of deployment to deploy the grain and oil supplies in order to relatively reduce the transportation costs of deployment.
3) Finally, we can use the minimum cost maximum flow theory to make a deployment plan to deploy the grain and oil supplies from the deployment warehouse to reserve station to achieve the overall effect of the minimum cost of deployment.
5. Application Examples
5.1. Example One
A province of china has a large grain and oil supplies deployment warehouse, with S representing, and has nine different regional grain and oil reserve stations, and they are respective as follows:![]() . Normally, this deployment warehouse can assure the grain and oil supplies requirements of the nine different reserve stations. However, when the emergency situation of grain and oil material shortage occurs, the grain and oil supplies deployed from deployment warehouse to reserve station cannot fully meet the needs of emergency situations, and this will cause great loss. So, we should establish the transport corridors between the reserve station and reserve station, between the deployment warehouse and reserve station. Then, we can select the deployment warehouse owning grain and oil supplies to deploy grain and oil supplies to the reserve station lacking grain and oil supplies according to the shortest distance between points so as to respond quickly in an emergency event. Table 1 shows the shortest transportation time and transport-path network between them [24] [25] .
. Normally, this deployment warehouse can assure the grain and oil supplies requirements of the nine different reserve stations. However, when the emergency situation of grain and oil material shortage occurs, the grain and oil supplies deployed from deployment warehouse to reserve station cannot fully meet the needs of emergency situations, and this will cause great loss. So, we should establish the transport corridors between the reserve station and reserve station, between the deployment warehouse and reserve station. Then, we can select the deployment warehouse owning grain and oil supplies to deploy grain and oil supplies to the reserve station lacking grain and oil supplies according to the shortest distance between points so as to respond quickly in an emergency event. Table 1 shows the shortest transportation time and transport-path network between them [24] [25] .
1) Path network diagram establishment
Regard the time that the vehicle cost between any two connected points as the “distance” between two points, and establish the path network diagram which connect every point. Figure 4 shows the path network diagram.
2) Distance matrix establishment
We can establish the distance matrix according to the path network diagram as follows:
![]()
Table 1. Transportation time and transport-path direction.
![]()
3) Model solution
Then, we use the Floyd algorithm to solve the model, and the solving results are follows:
![]()
Finally, we can obtain the shortest path between any two points from the solving results above. Then we can make appropriate deployment program of grain and oil in an emergency situations according to the shortest deployment time between any two points, and timely ensure that the demand of the areas for grain and oil.
5.2. Example Two
An area of China has seven grain and oil supplies deployment warehouses, they are respective as follows: A1, A2, A3, A4, A5, A6, A7. And the grain and oil reserves of them are respective as follows: 1.08 million tons, 960,000 tons, 1.32 tons, 1.26 million tons, 1.14 million tons, 1.38 million tons, 1.14 million tons. In addition, There are three grain and oil supplies reserve stations of three regions, they are respective as follows: V1, V2, V3, and their lowest grain and oil supplies requirements are follows: 2.76 million tons; 2.28 million tons; 1.32 million tons. When there is no emergency situation, that is to say, under normal circumstances, they are responsible for the deployment of grain and oil supplies from the seven employment warehouses to the three reserve stations [26] .
Table 2 shows the amount of grain and oil supplies of seven employment warehouses, the lowest grain and oil supplies requirements of the three grain and oil reserve stations, and the unit transportation costs of transporting unit suppliers from a deployment warehouse to a reserve station.
Table 3 shows the traffic capacity of road from a deployment warehouse to a reserve station.
1) Deployment network diagram establishment
Based on the above information, we establish the grain and oil deployment network diagram from the i deployment warehouse to the j reserve station as follows. Figure 5 shows the grain and oil deployment network diagram.
![]()
Figure 5. The deployment network diagram.
![]()
Table 2. Unit transportation costs (yuan).
![]()
Table 3. Road traffic capacity (0.01 million tons).
Further, the weight of arc from A1, A2, A3, A4, A5, A6, A7 to V1, V2, V3 is respective as follows: (300, 108), (240, 108), (345, 108), (195, 96), (165, 96), (300, 96), (195, 132); (240, 132), (300, 132), (75, 126), (105, 126), (195, 126), (195, 114), (105, 114); (240, 114), (300, 138), (300, 138), (375, 138), (75,114), (180, 114), (210, 114).
2) Model establishment
![]()
![]()
3) Model solution
Then, we use the minimum cost and maximum theory to solve the model. Table 4 shows the solving results of the model. Finally, we can obtain the optimal deployment scheme from the table above. And the minimum total transportation costs are 983.7 million yuan.
6. Conclusions
In the deployment process of grain and oil supplies, when there is an emergency situation, this paper uses the shortest path theory and develops a deployment plan to respond quickly according to the sudden and uncertainties of the emergencies, shortage of emergency supplies and other characteristics. It means that we can deploy the grain and oil supplies from source point to sink point along the shortest path based on the shortest path theory to timely ensure the deployment of emergency supplies.
In normal conditions, we can use the minimum cost maximum flow theory to develop the deployment plan of grain and oil supplies. It means that under the premise of meeting the minimum needs of grain and oil of different areas, we can use the lowest transport costs to convey the grain and oil materials to various reserve repositories as much as possible. We can also use the minimum cost maximum flow theory to develop the different deployment plan of grain and oil supplies according to the lowest grain and oil demand of each area in different periods.
And, when the urgency of emergency situation is in a lower level, we can combine the shortest path theory with the minimum cost maximum flow to make the deployment plan of grain and oil supplies. This can not only meet the needs of the destination but also reduce the whole transportation cost as much as possible.
Consequently, the application study of the graph theory in grain and oil deployment can provide some references to the actual deployment of grain and oil supplies.
NOTES
*Key project of Philosophy and Social Science Research in Beijing (09AbJG299); Key project of training plan of Beijing young top-notch talent (CIT & TCD201304109).