Local Study of Scalar Curvature of Cyclic Surfaces Obtained by Homothetic Motion of Lorentzian Circle ()
1. Introduction
Homothetic motion is general form of Euclidean motion. It is crucial that homothetic motions are regular motions. These motions have been studied in kinematic and differential geometry in recent years. An equiform transformation in the n-dimensional Euclidean space  is an affine transformation whose linear part is composed from an orthogonal transformation and a homothetical transformation add see [1] -[3] . Such an equiform transformation maps points
is an affine transformation whose linear part is composed from an orthogonal transformation and a homothetical transformation add see [1] -[3] . Such an equiform transformation maps points 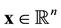 according to
according to
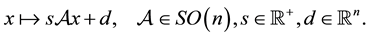 (1)
(1)
The number s is called the scaling factor. A homothetic motion is defined if the parameters of (1), including s, are given as functions of a time parameter t. Then a smooth one-parameter equiform motion moves a point x via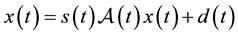 . The kinematic corresponding to this transformation group is called similarity kinematic. See [4] . Recently, the similarity kinematic geometry has been used in computer vision and reverse engineering of geometric models such as the problem of reconstruction of a computer model from an existing object which is known (a large number of) data points on the surface of the technical object [5] [6] . Abdel-All and Hamdoon studied a cyclic surface in
. The kinematic corresponding to this transformation group is called similarity kinematic. See [4] . Recently, the similarity kinematic geometry has been used in computer vision and reverse engineering of geometric models such as the problem of reconstruction of a computer model from an existing object which is known (a large number of) data points on the surface of the technical object [5] [6] . Abdel-All and Hamdoon studied a cyclic surface in . In this sense, they proved that such surface in
. In this sense, they proved that such surface in 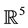 is in general contained in a canal hypersurface [7] . Solouma ( [8] - [10] ) studied locally some geometric problems on surfaces obtained by the equiform motion up to the first order. In Minkowski (semi-Euclidean) space, hyperbolas (Lorentzian circles) play role in Euclidean space [11] .
is in general contained in a canal hypersurface [7] . Solouma ( [8] - [10] ) studied locally some geometric problems on surfaces obtained by the equiform motion up to the first order. In Minkowski (semi-Euclidean) space, hyperbolas (Lorentzian circles) play role in Euclidean space [11] .
In this work we consider the homothetic motion of the hyperbolas(Lorentzian circles)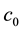 . Let
. Let 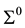 and
and 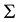 be two copies of Euclidean space
be two copies of Euclidean space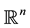 . Under a one-parameter homothetic motion of moving space
. Under a one-parameter homothetic motion of moving space 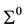 with respect to fixed space
with respect to fixed space , we consider
, we consider 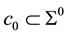 which is moved according homothetic motion. The point paths of the Lorentzian circle generate a cyclic surface X, containing the position of the starting Lorentzian circle. At any moment, the infinitesimal transformations of the motion will map the points of the Lorentzian circle
which is moved according homothetic motion. The point paths of the Lorentzian circle generate a cyclic surface X, containing the position of the starting Lorentzian circle. At any moment, the infinitesimal transformations of the motion will map the points of the Lorentzian circle 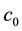 into the velocity vectors whose end points will form an affine image of
into the velocity vectors whose end points will form an affine image of ![]() that will be, in general, a Lorentzian circle in the moving space
that will be, in general, a Lorentzian circle in the moving space![]() . Both curves are planar and therefore, they span a subspace W of
. Both curves are planar and therefore, they span a subspace W of![]() , with
, with![]() . This is the reason because we restrict our considerations to dimension
. This is the reason because we restrict our considerations to dimension![]() .
.
Let ![]() be a parametrization of
be a parametrization of ![]() and
and ![]() the resultant surface by the homothetic motion. We consider a certain position of the moving space, given by
the resultant surface by the homothetic motion. We consider a certain position of the moving space, given by![]() , and we would like to obtain information about the motion at least during a certain period around
, and we would like to obtain information about the motion at least during a certain period around ![]() if we know its characteristics for one instant. Then we restrict our study to the properties of the motion for the limit case
if we know its characteristics for one instant. Then we restrict our study to the properties of the motion for the limit case![]() . A first choice is then approximate
. A first choice is then approximate ![]() by the first derivative of the trajectories. The purpose of this paper is to describe the cyclic surfaces obtained by the homothetic motion of the Lorentzian circle and whose scalar curvature
by the first derivative of the trajectories. The purpose of this paper is to describe the cyclic surfaces obtained by the homothetic motion of the Lorentzian circle and whose scalar curvature ![]() is constant.
is constant.
The proof of our results involves explicit computations of the scalar curvature ![]() of the surface
of the surface![]() . As we shall see, equation
. As we shall see, equation ![]() reduces to an expression that can be written as a linear combination of the hyperbolic functions
reduces to an expression that can be written as a linear combination of the hyperbolic functions ![]() and
and![]() ,
, ![]() , namely,
, namely, ![]() and
and ![]() and
and ![]() are functions on the variable t. In particular, the coefficients must vanish. The work then is to compute explicitly these coefficients
are functions on the variable t. In particular, the coefficients must vanish. The work then is to compute explicitly these coefficients ![]() and
and ![]() by successive manipulations. The authors were able to obtain the results using the symbolic program Mathematica to check their work. The computer was used in each calculation several times, giving understandable expressions of the coefficients
by successive manipulations. The authors were able to obtain the results using the symbolic program Mathematica to check their work. The computer was used in each calculation several times, giving understandable expressions of the coefficients ![]() and
and![]() .
.
This paper is organized as follows: In Section 2, we obtain the expression of the scalar curvature ![]() for the cyclic surfaces obtained by homothetic motion of Lorentzian circle. In successive Sections 3 and 4, we distinguish the cases
for the cyclic surfaces obtained by homothetic motion of Lorentzian circle. In successive Sections 3 and 4, we distinguish the cases ![]() and
and![]() , respectively. Finally, in Section 5 explicit examples of surfaces with
, respectively. Finally, in Section 5 explicit examples of surfaces with ![]() and
and ![]() are given.
are given.
2. Scalar Curvature of Cyclic Surfaces
In two copies![]() ,
, ![]() of semi-Euclidean 5-space
of semi-Euclidean 5-space![]() , we consider a unit Lorentzian circle
, we consider a unit Lorentzian circle ![]() in the
in the ![]() - plane of
- plane of ![]() centered at the origin and represented by
centered at the origin and represented by
![]()
Under a one-parameter homothetic motion of ![]() in the moving space
in the moving space ![]() with respect to fixed space
with respect to fixed space![]() . The position of a point
. The position of a point ![]() at “time” t may be represented in the fixed system as
at “time” t may be represented in the fixed system as
![]() (2)
(2)
where ![]() describes the position of the origin of
describes the position of the origin of ![]() at the time t,
at the time t,
![]() ,
, ![]() is a semi orthogonal matrix and
is a semi orthogonal matrix and ![]() provides the scaling factor of the moving
provides the scaling factor of the moving
system. For varying t and fixed![]() ,
, ![]() gives a parametric representation of the path (or trajectory) of
gives a parametric representation of the path (or trajectory) of![]() . Moreover we assume that all involved functions are of class
. Moreover we assume that all involved functions are of class![]() . Using the Taylor’s expansion up to the first order, the representation of the cyclic surface is
. Using the Taylor’s expansion up to the first order, the representation of the cyclic surface is
![]()
where ![]() denotes the differentiation with respect to t.
denotes the differentiation with respect to t.
As homothetic motion has an invariant point, we can assume without loss of generality that the moving frame ![]() and the fixed frame
and the fixed frame ![]() coincide at the zero position
coincide at the zero position![]() . Then we have
. Then we have
![]()
Thus
![]()
where![]() ,
, ![]() is a semi skew-symmetric matrix. In this paper all values of
is a semi skew-symmetric matrix. In this paper all values of ![]() and their derivatives are computed at
and their derivatives are computed at ![]() and for simplicity, we write
and for simplicity, we write ![]() and
and ![]() instead of
instead of ![]() and
and ![]() respectively. In these frames, the representation of
respectively. In these frames, the representation of ![]() is given by
is given by
![]()
or in the equivalent form
![]() (3)
(3)
For any fixed t in the above expression (3), we generally get an ellipse centered at the point![]() . The latter ellipse reduce to a Lorentzian circle subject to the following conditions
. The latter ellipse reduce to a Lorentzian circle subject to the following conditions
![]() (4)
(4)
where![]() . We now compute the scalar curvature of the cyclic surface
. We now compute the scalar curvature of the cyclic surface![]() . The tangent vectors to the parametric curves of
. The tangent vectors to the parametric curves of ![]() are
are
![]()
A straightforward computation leads to the coefficients of the first fundamental form defined by![]() ,
, ![]() ,
,![]() . The scalar product in the above equation in Lorentzian metric. According to the inner product this equation tends to
. The scalar product in the above equation in Lorentzian metric. According to the inner product this equation tends to![]() ,
, ![]() ,
, ![]() where
where
![]()
is the sign matrix. Then we get
![]()
Under the conditions (4) a computation yields
![]() (5)
(5)
and
![]() (6)
(6)
The Christoffel symbols of the second kind are defined by
![]()
where![]() ,
, ![]() are indices that take the value 1 or 2 and
are indices that take the value 1 or 2 and ![]() is the inverse matrix of
is the inverse matrix of![]() . From here, the scalar curvature of
. From here, the scalar curvature of ![]() is defined by
is defined by
![]()
Although the explicit computation of the scalar curvature ![]() can be obtained, for example, by using the Mathematica programme, its expression is some cumbersome. However, the key in our proofs lies that one can write
can be obtained, for example, by using the Mathematica programme, its expression is some cumbersome. However, the key in our proofs lies that one can write ![]() as
as
![]() (7)
(7)
The assumption of the constancy of the scalar curvature ![]() implies that (7) converts into
implies that (7) converts into
![]() (8)
(8)
Equation (8) means that if we write it as a linear combination of the functions ![]() namely,
namely,
![]() , the corresponding coefficients must vanish. From here, we will be able to
, the corresponding coefficients must vanish. From here, we will be able to
describe all cyclic surfaces with constant scalar curvature obtained by the homothetic motion of the Lorentzian circle![]() . As we will see, it is not necessary to give the (long) expression of
. As we will see, it is not necessary to give the (long) expression of ![]() but only the coefficients of higher order for the hyperbolic functions.
but only the coefficients of higher order for the hyperbolic functions.
We distinguish the cases ![]() and
and![]() .
.
3. Cyclic Surfaces with K = 0
In this section we assume that ![]() on the surface
on the surface![]() . From (7), we have
. From (7), we have
![]() (9)
(9)
We distinguish different cases that fill all possible cases (Note that we have all solutions by using the symbolic program Mathematica under the condition![]() ).
).
3.1. Case ![]()
At ![]() and
and![]() , the coefficients
, the coefficients ![]() for
for ![]() and the coefficients
and the coefficients ![]() for
for![]() . Also, since
. Also, since ![]() implies that
implies that![]() . But
. But ![]() if and only if
if and only if![]() . That’s means
. That’s means ![]() gives contradiction with Equation (9), so we have
gives contradiction with Equation (9), so we have![]() . We then conclude the following theorem.
. We then conclude the following theorem.
Theorem 3.1. Let ![]() be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle c0 and given by (3) under condition (4). Assume
be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle c0 and given by (3) under condition (4). Assume![]() , then
, then ![]() on the surface if and only if the following conditions hold:
on the surface if and only if the following conditions hold:
1) ![]()
2) ![]()
In particular, if ![]() for
for![]() , then circles generating the cyclic surfaces are coaxial.
, then circles generating the cyclic surfaces are coaxial.
3.2. Case![]() , But either
, But either ![]() or
or ![]() Is Not Zero
Is Not Zero
We have two possibilities:
1) If ![]() and
and![]() , then we have
, then we have![]() ,
, ![]() , the coefficients
, the coefficients ![]() for
for ![]() and the
and the
coefficients ![]() that’s means the equation
that’s means the equation![]() . From expression (6), we have two
. From expression (6), we have two
conditions
![]()
2) If ![]() and
and ![]() , then we have
, then we have![]() ,
, ![]() , the coefficients
, the coefficients ![]() for
for ![]() and
and
the coefficients ![]() that’s means the equation
that’s means the equation![]() . From expression (6), we have
. From expression (6), we have
![]()
Theorem 3.2. Let ![]() be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle c0 and given by (3) under condition (4) hold:
be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle c0 and given by (3) under condition (4) hold:
1) Assume ![]() and
and![]() , then
, then ![]() on the surface if and only if the following conditions
on the surface if and only if the following conditions
![]()
2) Assume ![]() and
and![]() , then
, then ![]() on the surface if and only if the following conditions
on the surface if and only if the following conditions
![]()
3.3. Case ![]()
If![]() , then we have
, then we have![]() , then coefficients
, then coefficients ![]() for
for![]() ,
, ![]() and
and ![]() for
for ![]() that’s means the equation (8) hold (i.e.,
that’s means the equation (8) hold (i.e.,![]() ). From expression (6), we have the two conditions
). From expression (6), we have the two conditions
![]()
Theorem 3.3. Let ![]() be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle c0 and given by (3) under condition (4). Assume
be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle c0 and given by (3) under condition (4). Assume![]() , then
, then ![]() on the surface if and only if the following conditions hold:
on the surface if and only if the following conditions hold:
1) ![]()
2) ![]()
4. Cyclic Surfaces with K ¹ 0
In this section we assume that the scalar curvature ![]() of the cyclic surface
of the cyclic surface ![]() obtained by the homothetic motion of Lorentzian circle
obtained by the homothetic motion of Lorentzian circle ![]() and given by (3) under condition (4) is a non-zero constant. The identity (8) writes then as
and given by (3) under condition (4) is a non-zero constant. The identity (8) writes then as
![]() (10)
(10)
Following the same scheme as in the case ![]() studied in Section 3, we begin to compute the coefficients
studied in Section 3, we begin to compute the coefficients ![]() and
and![]() . Let us put
. Let us put![]() .
.
1) CASE![]() . The coefficients
. The coefficients![]() ,
, ![]() and
and ![]() are
are
![]()
![]()
![]()
If![]() , we distinguish different possibilities:
, we distinguish different possibilities:
1.![]() ,
, ![]() ,
, ![]() , we conclude that
, we conclude that
![]()
2.![]() ,
, ![]() and
and![]() , we have the same result as in the above case.
, we have the same result as in the above case.
3.![]() ,
, ![]() and
and![]() , we have the same result as in cases from (1) and (2).
, we have the same result as in cases from (1) and (2).
From (1), (2) and (3) we have![]() ,
, ![]() ,
, ![]() under the following conditions
under the following conditions
![]()
4.![]() ,
, ![]() ,
,![]() . The coefficients
. The coefficients ![]() and
and ![]() are
are
![]()
![]()
If![]() , we have the following conditions
, we have the following conditions
![]()
2) CASE![]() , but either
, but either ![]() or
or ![]() is not zero. We have two possibilities:
is not zero. We have two possibilities:
1. If ![]() and
and![]() , then the coefficient
, then the coefficient![]() , implies that
, implies that![]() : contradiction
: contradiction
2. If ![]() and
and![]() , then the coefficient
, then the coefficient![]() , implies that
, implies that ![]() which gives a contradiction also.
which gives a contradiction also.
3) CASE![]() . The computations of
. The computations of ![]() implies that
implies that![]() , contradiction. As conclusion of the above reasoning, we conclude the following theorem.
, contradiction. As conclusion of the above reasoning, we conclude the following theorem.
Theorem 4.1. Let ![]() be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle
be a cyclic surfaces obtained by the homothetic motion of Lorentzian circle ![]()
and given by (3) under condition (4). Assume that![]() , then the scalar curvature
, then the scalar curvature ![]() or
or ![]()
on the surface if and only if the following conditions hold:
![]()
5. Examples of a Cyclic Surfaces with K = 0 and K ¹ 0
In this section, we construct two examples of a cyclic surfaces ![]() with constant scalar curvature
with constant scalar curvature ![]() and
and![]() . The first example corresponds
. The first example corresponds ![]() with the case
with the case![]() . In the second example, we assume
. In the second example, we assume ![]() and
and![]() .
.
Example 1. Case![]() . Let now the semi orthogonal matrix
. Let now the semi orthogonal matrix
![]() (11)
(11)
We assume ![]() and
and![]() , then
, then
![]()
Theorem 3.3 says that![]() . In Figure 1, we display a piece of
. In Figure 1, we display a piece of ![]() of Example 1 in axonometric view- point
of Example 1 in axonometric view- point![]() . For this, the unit vectors
. For this, the unit vectors ![]() and
and ![]() are mapped onto the vectors
are mapped onto the vectors ![]() and
and ![]() respectively [2] . Then
respectively [2] . Then
![]()
and
![]()
and both ![]() and
and ![]() parametrize domains of the
parametrize domains of the ![]() -plane.
-plane.
Example 2. Case![]() . Consider the semi orthogonal matrix
. Consider the semi orthogonal matrix
![]() (12)
(12)
Let ![]() and
and![]() , then
, then
![]()
Theorem 4.1 says that ![]() or
or![]() . In Figure 2, we display a piece of
. In Figure 2, we display a piece of ![]() of Example 2 in
of Example 2 in
axonometric viewpoint![]() . Then
. Then
![]()
and
![]()
and both ![]() and
and ![]() parametrize domains of the
parametrize domains of the ![]() -plane.
-plane.