Research of Impact of Geografical Latitute and Residual Ionospheric Noises on Informativeness of Measuring of Zenith Wet Delay of GPS Signals ()
1. Introduction
As it is noted in the work [1] , the microwave signals of satellite navigation systems are subjected to delay upon propagation in atmosphere. The major components of such delay are ionospheric and tropospheric delays. The ionospheric delay depends on frequency and almost can be removed.
The tropospheric delay reaches 2.5 m in zenith direction, or 25 m upon 5˚ elevation angle and hardly can be compensated. In its turn, the tropospheric delay contains hydrostatic component (by percentage reaching 90%) and wet delay. The hydrostatic delay can be determined by measuring the atmospheric pressure at the antenn location zone. The wet delay cannot be determined by only using the ground measurements. As it is noted in the work [1] , the zenith delay can be recalculated for direction of observation of satellite. Such a recalculation is carried out by using the mapping functions. If the elevation angle decreases, the delay of satellite signals will increase.
But in order to carry out the true analyses of error generated by such delays, one should know the amount of the wet delay in zenith direction. According to the work [1] , mostly used models of the wet delay are following:
1. Model of MOPS;
2. Hopfield’s model;
3. Mendes’s model.
In all abovementioned models the root mean square error decreases by the increase of the geographic latittude, because the tropics are featured by the higher level humidity, therefore, by big amount of wet delay.
As it was noted above, at present time the ionospheric delay of GPS signals can be removed on the whole. According to the work [2] , the delay of the signal upon propagation in ionosphere depends on the total amount of electrons along the path of the signal. That delay depends on frequency of signal, geographic location and current time. For the single frequency GPS receivers the model of Klobuchar has been developed. According to this mode, the zenith ionospheric delay at the moment 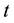 can be determined as
can be determined as
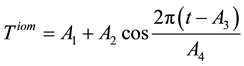 , (1)
, (1)
where : night-time value of zenith ionospheric;
: night-time value of zenith ionospheric;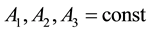 ;
; 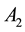 and
and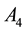 : parameters transferred by each GPS satellite in navigational massage depending on position of user, azimuth of the satellite, satellite’s height and local time. According to [3] , in single frequency GPS systems the ionospheric delay can cause the positioning error in amount of 5 - 15 m , but during the period of solar activity this error can reach 150 m . But as it is shown in [4] , upon use of double frequency GPS systems, using the frequencies
: parameters transferred by each GPS satellite in navigational massage depending on position of user, azimuth of the satellite, satellite’s height and local time. According to [3] , in single frequency GPS systems the ionospheric delay can cause the positioning error in amount of 5 - 15 m , but during the period of solar activity this error can reach 150 m . But as it is shown in [4] , upon use of double frequency GPS systems, using the frequencies 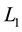 and
and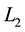 , utilization of linear combination of these signals makes it possible to remove the ionospheric delay by 99.9%.
, utilization of linear combination of these signals makes it possible to remove the ionospheric delay by 99.9%.
At the same time, the necessity of further increase of accuracy of GPS positioning systems requires more compensation of effect of ionospheric delay. The residual ionospheric delay, named also as an ionospheric delay of the second order, is generated as a result of interaction of ionosphere and the Earth’s magnetic field, and depends on the total amount of electrones in declined direction, parameters of the magnetic field, the angle between the magnetic field and direction of signal’s propagation.
As it is noted in the work [5] , at the geographical middle-latitude zones the most ionospheric effects increases in direction of the north to the south.
As it was noted above, the main non-removable delay GPS signal is the wet delay.
According to the work [6] , the zenith wet delay can be calculated by using the formula
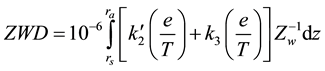 , (2)
, (2)
where  and
and : the emiprical coefficients;
: the emiprical coefficients;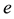 : pressure of water;
: pressure of water;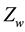 : compressibility factor of water vapors;
: compressibility factor of water vapors; : geocentrical radius of the site of installation of receiver’s antenn;
: geocentrical radius of the site of installation of receiver’s antenn;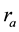 : geocentrical radius of the upper part of neutral atmosphere ;
: geocentrical radius of the upper part of neutral atmosphere ; : differential of
: differential of ![]() measured length.
measured length.
In model researches, the dimensionless coefficient ![]() is frequently used, determined as [6]
is frequently used, determined as [6]
![]() , (3)
, (3)
where![]() : the amount of precipitated water, determined as
: the amount of precipitated water, determined as
![]() . (4)
. (4)
According to the work [6] , there is the model of![]() , where such parameters as the geographic latitude and day of year are taken into account
, where such parameters as the geographic latitude and day of year are taken into account
![]() , (5)
, (5)
where![]() : the serial number of day of year;
: the serial number of day of year;
![]() .
.
Obviously, concerning the chosen day![]() , we have
, we have
![]() .
.
Taking into account the Formulas (3), (5), the ratio of signal/noise ![]() for determination of zenith wet delay may be calculated as
for determination of zenith wet delay may be calculated as
![]() , (6)
, (6)
where![]() : noises upon measurements, occurred due to ionospheric errors of the second order
: noises upon measurements, occurred due to ionospheric errors of the second order
![]() , (7)
, (7)
where![]() , upon
, upon![]() .
.
As it can be seen from Formula (7), ![]() increases by decrease of
increases by decrease of![]() . Taking into account Formulas (3), (6) and (7) we get
. Taking into account Formulas (3), (6) and (7) we get
![]() . (8)
. (8)
Now we consider the following optimization task. Assume that the measurements of ![]() are carried out and the authenticity of results of measurements is determined by Formula (8). The series of measurements are carried out at the different geographical latitudes
are carried out and the authenticity of results of measurements is determined by Formula (8). The series of measurements are carried out at the different geographical latitudes![]() . The number of measurements carried out of the latitude
. The number of measurements carried out of the latitude ![]() is determined as
is determined as![]() . The total amount of information received at the latitude
. The total amount of information received at the latitude ![]() can be determined as
can be determined as
![]() . (9)
. (9)
Integrating the Formula (9) along all the values of ![]() we get
we get
![]() . (10)
. (10)
Let us introduce the searched function
![]() . (11)
. (11)
which can be determined alternatively as
![]() , (12)
, (12)
or
![]() , (13)
, (13)
where![]() .
.
We assume that functions ![]() and
and ![]() meet following integral limitation condition
meet following integral limitation condition
![]() , (14)
, (14)
where![]() .
.
Taking into account the Formulas (10), (11) and (14) we can compose the following functional of unconditional variation optimization
![]() , (15)
, (15)
where![]() : Lagrange multiplier.
: Lagrange multiplier.
In order to determine the optimum function ![]() we use the Euler’s method, according to which following condition should be met
we use the Euler’s method, according to which following condition should be met
![]() . (16)
. (16)
Taking into the Formula (16) we get
![]() . (17)
. (17)
From the Formula (17) we can find
![]() . (18)
. (18)
Taking into consideration the Formulas (14) and (18) we find
![]() (19)
(19)
From the Formula (19) we get
![]() . (20)
. (20)
Using the Formula (20) we can get the value of the Lagrange multiplier
![]() . (21)
. (21)
Taking into consideration the Formulas (17) and (21) we get
![]() . (22)
. (22)
From the Formula (22) we find
![]() . (23)
. (23)
Therefore, upon function (23) the functional (15) reaches its extremum value.
In order to determine the type of extremum, we should calculate the following second derivative
![]() . (24)
. (24)
It is not difficult to check out that Formula (24) gains the negative value, i.e., upon condition (23) the target functional (15) reaches its maximum. Hence, upon the functional dependence (12) the informativeness of held measurements can reach its maximum. But its well-known that the increase of ![]() cause the decrease of
cause the decrease of![]() . Accordingly the type of the target functional (15) should be changed. Further, we assume, that the number of measurements in series is determined as
. Accordingly the type of the target functional (15) should be changed. Further, we assume, that the number of measurements in series is determined as
![]() , (25)
, (25)
where![]() .
.
Taking into account (17) and (15) we get
![]() . (26)
. (26)
Using the above described method we can determine that the functional (26) will reach its maximum upon condition
![]() . (27)
. (27)
In this case in order to determine the type of extremum we should compute the following second derivative ![]() (28)
(28)
From Formula (28) we get
![]() .
.
Because Formula (28) reaches the negative value, the maximum informativeness could be reached upon condition (12), but the number of measurements in series can be determined in line with Formula (25).
Hence, informativeness of measurements carried out on geographical latitudes to determine the zenith wet delay can reach its maximum upon meeting of two conditions:
1. The total amount of precipitated water ![]() should decrease by the increase of geographical latitude;
should decrease by the increase of geographical latitude;
2. The number of measurements in series should decrease by the increase of latitude.