Predicting of the Fibrous Filters Efficiency for the Removal Particles from Gas Stream by Artificial Neural Network ()
1. Introduction
Concern with the increasing air pollution has stimulated the development of new techniques that operate in the efficiency of solid-gas separation, mainly for smaller particles. Filtration by fibrous filters is one of the most widely used techniques to capture fine particles from a gas stream. The process takes place by passing the aerosol through the filter media, so that the particles will be deposited on the filter surface [1]. A fibrous filter consists of many threadlike fibers, of varying sizes, positioned more or less normal to the direction of the fluid flow. The fluid passes through the regions between the fibers and particles, which are suspended in the fluid, are removed by their collision and attachment to the fiber surface. The fibrous filters are notable for their usefulness in removing fine particles from aerosols at low cost and easy implementation [2].
The performance of filtration is evaluated, essentially, for two parameters, the pressure drop and collection efficiency. For this, several authors have theoretically studied the efficiency of particle deposition on fibers. Lee and Liu [3] developed a theoretical analysis of filtration mechanisms, focusing on maximum penetration. They proposed an improvement in diffusion and interception filtration efficiencies. Fardi and Liu [4] determined nu-merically the single fiber efficiency of rectangular electret fibers owing to Brownian diffusion. Kirsh [5] studied the deposition of nanoparticles on model filters with different porosities. From the numerical results using the convection-diffusion equation, the efficiency was determined for particle deposition on a fiber whose results agreed with experimental data. Dunnett and Clement [2] developed an accurate numerical method for calculating diffusive and interceptive deposition on a fiber in fibrous filters. By including semi-empirical correction factors in a correlation, Liu and Rubow [6] extended the correlations of Lee and Liu [3] for submicron particles. Recently, Silva et al. [7] numerically studied the diffusive deposition of aerosol nanoparticles on a single fiber. Other authors like Kirsh [8], Steffens and Coury [9], Walsh et al. [10] and Wang et al. [11] also worked with theoretical analysis of the efficiency of particle deposition on a fiber.
Thus, it is evident from the works above that theoretical studies are of prime importance for understanding the performance of fibrous filters. Also, it is important to observe that, combined with artificial neural network (ANN), predictions from parameters of this process may become an important factor for innovation and development of new techniques. In addition, ANNs have several advantages that make them attractive tools: they can be trained to learn from examples; are easily updated and generalized; possess a large degree of freedom and accurate prediction at high speed [12]-[14]. ANNs possess the ability to identify a relationship from given patterns and this makes it possible to solve large-scale complex problems such as nonlinear mathematical models.
Recently, ANNs models have been successfully applied to various branches of science and technology, such as medicine [15] [16], mathematics and engineering [17], among others. However, these references failed to mention that ANNs have been applied to predicting the collection efficiency of fibrous filters; this being the prime moti-vation for the present study.
The objective of this work is to investigate the possibility of using a neural network to directly assess the single fiber efficiency. Thus, a much more robust measurement method can be developed. For this, in order to construct a database for developing a neural model, a mathematical model is implemented and numerical results are obtained for several Peclet numbers and packing density, which are important parameters in this process.
2. Modelling for Single Fiber Efficiency
This section aims to present the mathematical modelling to simulate the process of particle deposition on a single fiber to construct a database for an ANN model.
As the structure of fibrous filters is complex, many works have adopted cell models in which fluid flow equations are solved in a two dimensional cell surrounding the single fiber, where the boundary conditions take into account neighboring fibers [2] . Thus, the cell model was adopted to determine the flow field. The geometry is illustrated in Figure 1, where a (=1) is the dimensionless fiber radius, b (=a−1/2) is the dimensionless cell radius that is determined by the filter packing density a and U is the flow velocity scale [7] [18] [19] .
2.1. The Physical Model for Single Fiber Efficiency
In this study, the deposition of aerosol particles in fibrous filters is considered to occur exclusively because of diffusion, which is one of the major particle collection mechanisms, especially when dealing with smaller particles (see [2] [3] [18]).
The single fiber efficiency is mathematically expressed by
![]() (1)
(1)
where n is the particle concentration and Pe is the Peclet number.
To determine numerically the value of the integral in Equation (1), the following dimensionless convection diffusion partial differential equation is utilized, which in polar coordinates r and θ is given by [3]
![]() (2)
(2)
where ur and uθ are, respectively, the radial and angular components of the gas velocity, expressed as
![]() and
and![]() (3)
(3)
with Ψ being the dimensionless Kuwabara function [5] [18].
For fibrous filtration, the third term on the right-hand side of Equation (2) is much smaller than the other terms and can be neglected to give [2] [3]
![]() (4)
(4)
The adopted boundary conditions are
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
2.2. Numerical Procedure
Equation (4) associated with the boundary conditions (5)-(7) was discretized by finite-difference methodology on a staggered grid system; the diffusive terms were approximate by second order central differences and the non-linear convection terms were approximated by the TOPUS upwind scheme [20], which was expressed in this work as
![]() (8)
(8)
where f is a boundary face of a computational cell (see Figure 2). The quantity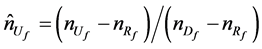 ,
,
corresponds to the normalized variables of Leonard [21] . The coefficients c1, c2 and c3 are expressed as c1 = −2b + 1, c2 = (5b − 10)/4 and c3 = (−b + 10)/4, where b is an adjustable real parameter chosen in the interval [−2, 2] to attend the total variation diminishing (TVD) condition of Harten [22] . The neighboring nodes Df (Downstream), Uf (Upstream) and Rf (Remoteupstream) of a computational face f are prescribed according to the advection velocity vf (ur or uq) at this face, as can be observed in Figure 2. The TOPUS scheme was chosen for
![]()
Figure 2. Schematic representation to obtain approximations of the con- vective terms.
this study since the use of conventional schemes (central differences and first order upwind) has been unsatisfactory for predicting single fiber efficiency in the range 100 £ Pe £ 165, 0.2 £ a £ 0.3.
The linear system resulting from the discretization of Equation (4) was solved by the Gauss-Seidel iteration procedure. The numerical results were compared favorably with experimental data of literature and published in [7] [19].
3. Artificial Neural Network
In this section, the basic concepts of ANNs, the back propagation algorithm and a new neural model for predic- ting h, in the process of removing aerosol particles, are introduced.
3.1. Theoretical Basis
In short, ANNs are a form of artificial intelligence composed of a network of connected nodes (neurons). Formally, an ANN can be defined as nonlinear mapping of an input onto an output vector space. This is achieved through layers of neurons in which the input coordinates are summed according to specific weights and biases to produce a single output. Finding suitable architecture for ANNs is extremely critical; most works in the literature use trial and error to adjust the parameters of a neural network (see, for example, [12] [23]-[25].)
In this study, a four-layer feed-forward ANN with two hidden layers was employed and the back propagation algorithm was used for the training. No recursiveness was adopted here, that is, the input vector of a specific neuron layer was formed only by the values of the preceding layer. A schematic representation of a typical ANN structure is depicted in Figure 3.
The notation in a feed-forward network is as follows. If the activation function of i-th neuron in the j-th layer is indicated by Fi j(.), its output si, j can be calculated from outputs of the preceding layer si j-1 and from the corre-sponding biases bi,j and weights wi,k,j-1 (the second subscript k indicates the neuron in the (j − 1)-th layer from which the connection is being established), according to
![]() (9)
(9)
After denoting the input and output network values by σi, i = 1, 2, 3, 4 and ξj, j = 1, 2, respectively, the mapping relationship of one onto the other can then be done by applying Equation (9). For instance, the mapping in Figure 3 reads
![]() (10)
(10)
Equation (10) makes it clear that the relationship between σi and ξj is unambiguously defined by choosing the activation functions and by setting the biases and weights. One very important characteristic of ANNs, among others, is the so-called learning potential, that is, the possibility of adjusting the biases and weights through a convenient training rule to closely reproduce pre-assigned pairs of input/output values. Back propagation is probably the most used training heuristic and it is particularly well adapted to feed-forward architecture. It is based on the iterative application of a discrete gradient descent algorithm, computed from the first derivatives of a conveniently defined error function whose arguments are the parameters of the network (weights and biases). In general, the basic steps of the back propagation procedure, which is implemented in this work, are the following [26]:
![]()
Figure 3.Schematic representation of a typical feed-forward four-layer ANN, showing the mapping of a four input coordinate onto a two output coordinate vector [26] .
1) Initialize the ANN's parameters bi,j and wi,k,j with random numbers;
2) Take the p-th (σip, ξip) pair from a training data set with pre-assigned input/output pairs;
3) Calculate the outputs with the same input and form the pair (σip, ξip);
4) Evaluate the error e between the desired and the obtained output values according to the L2 norm
![]() (11)
(11)
5) Calculate the derivatives of the error with respect to bi,j and wi,k,j;
6) Modify the ANN parameters according to the steepest descent strategy and a specified learning rate γ
![]() (12)
(12)
![]() (13)
(13)
7) Iterate from 2 to 5, by successively modifying bi,j and wi,k,j, until a defined number of learning epochs (cycles) or a convenient stopping criterion has been achieved.
The performance of an ANN is affected by internal architecture (number of hidden layers and number of neurons in each one) and type of interconnections (feed-forward, recursiveness, winner-take-all, etc.). The exact shape of the activation function has limited effects on the overall performance and is usually set according to the needs of the training heuristics (a sigmoid function in the case of the back propagation method). There is no general mathematical theory but rather a number of empirical rules that must be considered when constructing such models.
3.2. Neural Modelling for Single Fiber Efficiency
The ANN implemented in this work has two inputs and one output. Various architectures were trained and tested; the neural model that provided good results, obtained by trial and error, was that containing two intermediate layers with six and three neurons. The number of neurons in the intermediate layers was adjusted to enable the ANN to learn complex tasks for the gradual extraction of significant information from the inputs [27] [28]. The activation functions used in the neural network were the tangent sigmoid in the intermediate layers and a linear function in the output layer, expressed respectively as
![]() (14)
(14)
![]() (15)
(15)
where 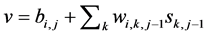 is the activation potential of the above functions.
is the activation potential of the above functions.
The neuron of the output layer is responsible for estimating single fiber efficiency (η). The training procedure uses the acquisition of the Peclet number (Pe) and packing density (α) for the filter to a sufficient level for inference of the η. Two numerical simulations were performed with Pe and α varying uniformly in the ranges: a) 20 ≤ Pe ≤ 80 and 0.1 ≤ α ≤ 0.2; and b) 100 ≤ Pe ≤ 165 and 0.2 ≤ α ≤ 0.3. Equation (1) was used for estimating the η.
In both simulation cases, the input data matrix has 2 lines for 165 columns with the line number correspon- ding to the number of inputs (Pe and α) and the column to the examples used in the training of the ANN; each one corresponds to a known and fixed value of the η. The output matrix has 1 line for 165 columns, where 1 is the number of desired output and 165 is the number of examples. Generalization was considered: 88 different examples, from those used in the training process, were presented to the ANN in the first simulation; and 66 examples in the second simulation. Therefore, in the first calculation, 253 pairs of input/output values were obtained to construct the database, and in the second calculation 231 pairs were employed. The division of the examples in the training and test sets was done randomly and some divisions were tested. The ANN results for all the tested divisions were shown to be practically equal, with the same correlation coefficients for the data.
4. Results and Discussion
The purpose of this section is that it presents the training error of neural network developed and the results obtained for the data of the test.
The results of the training of the ANN have shown that it is capable of reproducing the input/output relationship of the training set data. To evaluate the generalization capacity of the ANN, the characteristic data of new nu-merical tests were presented to the neural networks and a good correlation between the input and output data was observed.
In attempting to reduce the error in a reasonable time, optimization of the ANN parameters (learning rate, epochs and number of neurons in the intermediate layers) was performed. The learning rate used in both tests was 0.1 and 12 × 104 epochs were considered, with a training time of 36 minutes for the first case, and 44 minutes for the second one. As can be observed from Figure 4 and Figure 5, the training error for both ANNs behaved as expected like O (10−4).
Figure 6 and Figure 7 present the estimated data for η, calculated by the ANN after the training period, considering the examples in the test set of the first and second range. The dots in the graphs are the values determined by the ANN. For the first range (see Figure 6), the straight line that best represents the correlation between the values of η estimated by the ANN and the numerical results is y = 1.0047x − 0.0012 [29] [30] . The Pearson r-squared correlation coefficient (R2) between the numerical values and the ANN values was 0.9996, showing that there was a strong relationship between the input and output data provided by the ANN; whereas, in the second range, the best representation for η is y = 1.0021x − 0.0003 with a correlation coefficient of 0.9995. These results indicate that training of the ANNs was successfully accomplished.
![]()
Figure 4.Error during the training of the ANN. Estimate for single fiber efficiency in the range 20 ≤ Pe ≤ 80; 0.1 ≤ α ≤ 0.2.
![]()
Figure 5.Error during the training of the ANN. Estimate for single fiber efficiency in the 100 ≤ Pe ≤ 165; 0.2 ≤ α ≤ 0.3.
![]()
Figure 6. Comparison between the values estimated by the ANN and the numerical values for the single fiber efficiency in the range 20 ≤ Pe ≤ 80; 0.1 ≤ α ≤ 0.2.
![]()
Figure 7. Comparison between the values estimated by the ANN and the numerical values for the single fiber efficiency in the range 100 ≤ Pe ≤ 165; 0.2 ≤ α ≤ 0.3.
In summary, the results obtained through the ANN for the test set examples were quite satisfactory, with maximum relative errors of 1.7% for the first case and 0.9% for the second case.
Table 1 presents (for some test set examples) the responses of the ANN for η in the two ranges, where good agreement can be seen between the numerical η (ηNumeric) and the η estimated by the ANN (ηANN).
![]()
Table 1. Response of the ANN to the η in two ranges of Pe and α.
5. Conclusions
Artificial neural models were trained with data derived from numerical simulations in order to determine smaller particle capture efficiency in a single fiber. To construct a database, a sufficient number of examples were per-formed, from which the ANN parameters (weights and biases) were adjusted. A model was developed to map the parameters Pe and α with the aim of estimating the single fiber efficiency, η. The developed ANN was shown to be capable of estimating correct values for fiber efficiency from examples not contemplated in the training.
From this research, it can be inferred that, in the context of fiber filter efficiency, the developed neural model is an effective tool for performing nonlinear mapping of the parameters. The simplicity and efficiency of the pro-posed neural approach indicates that the present methodology can be effectively used in the process studied. Furthermore, it should be emphasized still that, although numerical data have been used in this work, the results obtained suggest that if the experimental data are available, these data could have been used to train the neural network which would produce a very powerful prediction tool.
Acknowledgements
The authors wish to express their thanks to the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq-Grants No. 475390/2011-3) for the financial support.
Nomenclature
Greek
NOTES
*Valdemir Garcia Ferreira (in memoriam).