The Global Attractors for a Nonlinear Viscoelastic Wave Equation with Strong Damping and Linear Damping and Source Terms

Liang Guo^*, Zhaoqin Yuan, Guoguang Lin

Department of Mathematics, Yunnan University, Kunming, China.

DOI: 10.4236/ijmnta.2015.42010                

Abstract

In this paper, firstly, some priori estimates are obtained for the existence and uniqueness of solutions of a nonlinear viscoelastic wave equation with strong damping, linear damping and source terms. Then we study the global attractors of the equation.

Keywords

Global Attractors, Viscoelastic Equation, Priori Estimates

1. Introduction

We know that viscoelastic materials have memory effects. These properties are due to the mechanical response influenced by the history of the materials. As these materials have a wide application in the natural science, their dynamics are of great importance and interest. The memory effects can be modeled by a partial differential equation. In recent years, the behaviors of solutions for the PDE system have been studied extensively, and many achievements have been obtained. Many authors have focused on the problem of existence, decay and blow-up for the last two decades, see [1] -[5] . And the attractors are still important contents that are studied.

In [6] , R.O. Araújo, T. Ma and Y.M. Qin studied the following equation

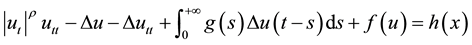(1.1)

and they proved the global existence, uniqueness and exponential stability of solutions and existence of the global attractor.

In [7] , Y.M. Qin, B.W. Feng and M. Zhang considered the following initial-boundary value problem:

(1.2)

where 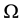is a bounded domain of 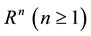with a smooth boundary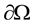, 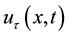(the past history of u) is a given datum which has to be known for all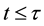, the function g represents the kernel of a memory,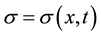

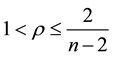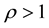is a non-autonomous term, called a symbol, and ρ is a real number such that if; if

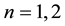. They proved the existence of uniform attractors for a non-autonomous viscoelastic equation with a past history. For more related results, we refer the reader to [8] -[14] .

In this work, we intend to study the following initial-boundary problem:

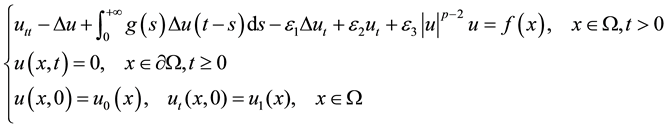(1.3)

where and 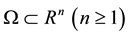is a bounded domain with smooth boundary,

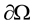if; if, for the problem (1.3), the memory term

replaces, and we consider the strong damping term, the li-

near damping term and source terms. We define

A direct computation yields

Thus, the original memory term can be written as

and we get a new system

(1.4)

(1.5)

with the initial conditions

(1.6)

and the boundary conditions

(1.7)

The rest of this paper is organized as follows. In Section 2, we first obtain the priori estimates, then in Section 3, we prove the existence of the global attractors.

For convenience, we denote the norm and scalar product in by and, let,.

2. The Priori Estimates of Solution of Equation

In this section, we present some materials needed in the proof of our results, state a global existence result, and prove our main result. For this reason, we assume that

(G1) is a differentiable function satisfying;

(G2);

(G3) There exists a constant such that,;

Lemma 1. Assume (G1), (G2) and (G3) hold, let

and, , , then the solution of Equation (1.3) satisfies

and

(2.1)

here, thus there exists and, such that

(2.2)

Proof. We multiply with both sides of equation and obtain

By using Holder inequality, Young’s inequality and Poincare inequality, we get

(2.3)

and

(2.4)

and

(2.5)

For the first term on the right side (2.5), by using (G1), (G2) and (G3), we have

(2.6)

where

(2.7)

For the second term on the right side (2.5), by using Holder inequality and Young’s inequality, we get

(2.8)

So, we have

(2.9)

By using Poincare inequality, we obtain

(2.10)

and

(2.11)

and

(2.12)

By using Holder inequality and Young’s inequality, we obtain

(2.13)

Then, we have

(2.14)

That is

(2.15)

Next, we take proper, such that

(2.16)

Taking, then

(2.17)

where, by using Gronwall inequality, we obtain

(2.18)

From, according to Embedding Theorem then, let, so we have

Then

So, there exists and, such that

Lemma 2. Assume (G1), (G2) and (G3) hold, let

and, , , then the solution of Equation (1.3) satisfies and

(2.19)

Here, thus there exists and, such that

(2.20)

Proof. We multiply with both sides of equation and obtain

(2.21)

By using Holder inequality, Young’s inequality and Poincare inequality, we get

and

(2.22)

and

(2.23)

For the first term on the right side (2.23), by using (G1), (G2) and (G3), we have

(2.24)

where

(2.25)

For the second term on the right side (2.23), by using Holder inequality and Young’s inequality, we get

(2.26)

so, we have

By using Poincare inequality, we have

(2.27)

and

(2.28)

And using Interpolation Theorem, we have

(2.29)

By using Holder inequality and Young’s inequality, we have

(2.30)

Then, we have

That is

(2.31)

Next, we take proper, such that

(2.32)

Taking, then

(2.33)

where, by Gronwall inequality, we have

(2.34)

From, according to Embedding Theorem, then, let, so, we have

then

So, there exists and, such that

3. Global Attractors

Theorem 1. Assume (G1), (G2) and (G3) hold, let

and, , , so Equation (1.3) exists a unique smooth solution

Proof. By the method of Galerkin and Lemma 1 and Lemma 2, we can easily obtain the existence of solutions. Next, we prove the uniqueness of solutions in detail.

Assume that are two solutions of equation, let, then, the two equations subtract and obtain

(3.1)

where

(3.2)

By multiplying the equation by and integrating over, we get

(3.3)

here

(3.4)

and

(3.5)

by using (G1), (G2) and (G3), we have

(3.6)

By using Poincare inequality, we have

(3.7)

and

(3.8)

By using Holder inequality, Young’s inequality and Poincare inequality, we have

(3.9)

then, we have

(3.10)

That is

(3.11)

Taking, then

(3.12)

By using Gronwall inequality, we have

(3.13)

So we get, the uniqueness is proved.

Theorem 2. Let X be a Banach space, and are the semigroup operator on X., , , here I is a unit operator. Set satisfy the follow conditions.

1) is bounded, namely, , it exists a constant, so that

2) It exists a bounded absorbing set, namely, , it exists a constant, so that

3) When, is a completely continuous operator A.

Therefore, the semigroup operators exist a compact global attractor.

Theorem 3. Under the assume of Theorem 1, equations have global attractor

where, is the bounded absorbing set of

and satisfies

1),;

2), here and it is a bounded set,

Proof. Under the conditions of Theorem 1, it exists the solution semigroup, here,.

1) From Lemma 1 to Lemma 2, we can get that is a bounded set that includes in

the ball,

This shows that is uniformly bounded in.

2) Furthermore, for any, when, we have

So, we get is the bounded absorbing set.

3) Since is tightly embedded, which means that the bounded set in is the tight set in, so the semigroup operator is completely continuous.

So, the semigroup operators exist a compact global attractor A. The proof is completed.

Acknowledgements

The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.

Funding

This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Messaoudi, S.A. (2003) Blow Up and Global Existence in a Nonlinear Viscoelastic Wave Equation. Mathematische Nachrichten, 260, 58-66. http://dx.doi.org/10.1002/mana.200310104
[2]	Cavalcanti, M.M., Domingos Cavalcanti, V.N. and Ferreira, J. (2001) Existence and Uniform Decay for Nonlinear Viscoelastic Equation with Strong Damping. Mathematical Methods in the Applied Sciences, 24, 1043-1053. http://dx.doi.org/10.1002/mma.250
[3]	Berrimi, S. and Messaoudi, S.A. (2006) Existence and Decay of Solutions of a Viscoelastic Equation with a Nonlinear Source. Nonlinear Analysis: Theory, Methods & Applications, 64, 2314-2331. http://dx.doi.org/10.1016/j.na.2005.08.015
[4]	Lu, L.Q. and Li, S.J. (2011) Cauchy Problem for a Nonlinear Viscoelastic Equation with Nonlinear Damping and Source Term. Applied Mathematics Letters, 24, 1275-1281. http://dx.doi.org/10.1016/j.aml.2011.01.009
[5]	Kafini, M. and Mustafa, M.I. (2014) Blow-Up Result in a Cauchy Viscoelastic Problem with Strong Damping and Dispersive. Nonlinear Analysis: Real World Applications, 20, 14-20. http://dx.doi.org/10.1016/j.nonrwa.2014.04.005
[6]	Araújo, R.O., Ma, T. and Qin, Y.M. (2013) Long-Time Behavior of a Quasilinear Viscoelastic Equation with Past History. Journal of Differential Equations, 254, 4066-4087. http://dx.doi.org/10.1016/j.jde.2013.02.010
[7]	Qin, Y.M., Feng, B.W. and Zhang, M. (2014) Uniform Attractors for a Non-Autonomous Viscoelastic Equation with a Past History. Nonlinear Analysis: Theory, Methods & Applications, 101, 1-15. http://dx.doi.org/10.1016/j.na.2014.01.006
[8]	Qin, Y.M., Zhang, J.P. and Sun, L.L. (2013) Upper Semicontinuity of Pull Back Attractors for a Non-Autonomous Viscoelastic Equation. Applied Mathematics and Computation, 223, 362-376. http://dx.doi.org/10.1016/j.amc.2013.08.034
[9]	Conti, M. and Geredell, P.G. (2015) Existence of Smooth Global Attractors for Nonlinear Viscoelastic Equations with Memory. Journal of Evolution Equations. http://dx.doi.org/10.1007/s00028-014-0270-2
[10]	Cavalcanti, M.M., Domingos Cavalcanti, V.N., Prates Filho, J.A. and Soriano, J.A. (2001) Existence and Uniform Decay Rates for Viscoelastic Problems with Non-Linear Boundary Damping. Differential and Integral Equations, 14, 85-116.
[11]	Munoz Rivera, J.E., Lapa, E.C. and Barreto, R. (1996) Decay Rates for Viscoelastic Plates with Memory. Journal of Elasticity, 44, 61-87. http://dx.doi.org/10.1007/BF00042192
[12]	Wu, S.T. (2011) General Decay of Solutions for a Viscoelastic Equation with Nonlinear Damping and Source Terms. Acta Mathematica Scientia, 31, 1436-1448. http://dx.doi.org/10.1016/S0252-9602(11)60329-9
[13]	Ma, T.F. and Narciso, V. (2010) Global Attractor for a Model of Extensible Beam with Nonlinear Damping and Source Terms. Nonlinear Analysis: Theory, Methods & Applications, 73, 3402-3412. http://dx.doi.org/10.1016/j.na.2010.07.023
[14]	Qin, Y., Deng, S. and Schulze, W. (2009) Uniform Compact Attractors for a Nonlinear Non-Autonomous Equation of Viscoelasticity. Journal of Partial Differential Equations, 22, 153-198.