Construction of Three Quadrature Formulas of Eighth Order and Their Application for Approximating Series

Bogusław Bożek, Wiesław Solak, Zbigniew Szydełko

Faculty of Applied Mathematics, AGH University of Science and Technology, Cracow, Poland.

DOI: 10.4236/am.2015.66095                

Abstract

In this paper, three types of three-parameters families of quadrature formulas for the Riemann’s integral on an interval of the real line are carefully studied. This research is a continuation of the results in the [1]-[3]. All these quadrature formulas are not based on the integration of an interpolant as so as the Gregory rule, a well-known example in numerical quadrature of a trapezoidal rule with endpoint corrections of a given order (see [4]). In some natural restrictions on the parameters we construct the only one quadrature formula of the eight order which belongs to the first, second and third family. For functions whose 8th derivative is either always positive or always negative, we use these quadrature formulas to get good two-sided bound on . Additionally, we apply these quadratures to obtain the approximate sum of slowly convergent series , where .

Keywords

Quadrature and Cubature Formulas, Numerical Integration

1. Introduction

We consider the three-parameters families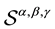, , 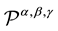of quadrature formulas for the integral

. These quadratures are linear combinations of the quadrature investigated in papers [1] - [3]

respectively. The error estimates are calculated in dependence of the parameters, , and then in some natural restrictions on them these are investigated the quadrature formulas of the 8th order. The desired con- clusions are made by means of properties of Peano kernels using substantially well-known error formulas. We construct the only one quadrature formula of the eight order which belongs to the family, the only one quadrature formula of the eight order too, which belongs to the family and the only one quadrature for- mula of the eight order too, which belongs to the family. Because of the Peano kernels for these qua- dratures have different signs, for functions whose 8th derivative is either always positive or always negative we use these quadrature formulas to get good bounds on. So, by suitable choice of parameters one can increase quadrature order from two or four respectively to eight.

2. The Three-Parameters Family of Quadrature Formulas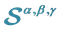

We consider family of quadrature formulas given by

(1)

for integral. This family generalizes the family discussed in [1] , here it is enough to put, ,.

For arbitrary, , the quadrature formula is of the second order. The error

for the polynomials is equal

If a triple is a root of the polynomial the range of quadrature

formula increases. These triples we can write in the form with

where. Then every is of the fourth order, and moreover

If the pair is a root of the polynomial then the range of

quadrature increases as before. We can write these pairs in the form where

for.

Every quadrature is of the six order but we must restrict the interval for. The quadrature

nodes belongs to interval only for. Graphs of the functions

and are presented on the Figure 1.

In this case we have

The six order Peano kernel where. This

kernel is a periodic function with period h and on every interval is symmetrical respect to

its midpoint. So, it is enough to define it on the interval:

(2)

The kernel is negative for and positive for. After numerical calculation we conclude that, (see Figure 2).

Figure 1. Graphs of and.

Figure 2. Graph of the kernel for (,).

The integral of the six order Peano kernel takes form

(see Figure 3).

From Peano theorem (see [5] ) the error

(3)

for any function and, where. Moreover, using Peano theorem we can prove the following:

Theorem 1. If, , function, and has constant sign on interval

, then

Figure 3. Graph of the function.

(4)

if is non-negative on interval, and

(5)

if is non-positive on interval.

Proof. Assume that. From the formula (3), because of and, we have

Similarly

because of and. □

The function has one root

. Lets put

,. The quadrature

formula is of the eight order and

The eight order Peano kernel where. This kernel

is a periodic function with period h and on every interval symmetrical with respect to its

midpoint. So us for, it is enough to define it on the interval:

(6)

(see Figure 4).

This kernel is non-negative, moreover

From the Peano theorem (see [5] ) we obtain for any function the expression on the error

(7)

where.

3. The Three-Parameter Family of Quadrature Formulas

We consider the family of quadrature formulas of the form

(8)

where

, , is the trapezoidal rule, and, , are para-

Figure 4. Graph of the fragment of the kernel for (,).

meters. Particular cases and are investigated in the paper [2] and, . We are proved that and with

where and (see Figure 5) are of the six order. If we define the error

we can compute for the polynomials

where

So, for every the quadrature is of the six order. Let

With the range of quadrature formula increases. The quadrature is of the eight order but the expression takes a very complicated form.

The eight order Peano kernel where. This kernel

Figure 5. Graphs of the sequences, ,.

is a symmetrical function respect to the point, so it is enough to define it on the interval:

(9)

where

and. On the Figure 6 we have graphs of the kernels for. For any n the kernel

is non-positive, moreover the integral

in the case and

Figure 6. Graphs of the kernels for n = 4, 5, 6.

if. From the Peano theorem (see [5] ) we obtain for any function the expression on the error

(10)

where and for all n.

A Complex Quadrature Formula

Let, the step and the nodes . The integral can be written in the form, where. To each integral we apply the quadrature (8):

(11)

where now,

, ,. Next we define

(12)

Obviously. For every, the quadrature formula is of the six order and is of the eight order. The Peano kernel for the quadrature formula is a periodic function with period k and on every interval is symmetrical with respect to its midpoint. The quadrature formula (12) has nodes.

Because of Peano kernels for quadrature formulas, have different signs, we have the following theorem.

Theorem 2. If function, and the derivative has constant sign on interval, then

(13)

if is non-negative on the interval, and

(14)

if is non-positive on the interval.

Proof. Assume that. From the formula (7) we have

because of and. Similarly from the formula (10):

because of and. □

4. The Three-Parameter Family of Quadrature Formulas

We consider the family of quadrature formulas of the form

(15)

where

, , is the midpoint rule, and, , are parameters. Parti-

cular cases and are investigated in the paper [3] and,

. We are proved that and with

where

are of the six order. If we define the error we can compute for the polynomials

where

So, for every the quadrature is of the six order. Let

(see Figure 7).

With the range of quadrature formula increases. The quadrature is of the eight order but the expression takes a very complicated form.

The eight order Peano kernel where. This kernel is a symmetrical function respect to the point, so it is enough to define it on the interval:

Figure 7. Graphs of the sequences, ,.

(16)

where

and. On the Figure 8 we have graphs of the kernels for. For any n the kernel

is non-negative, moreover the integral

(17)

where

Figure 8. Graphs of the kernels for n = 4, 5, 6.

and

From the Peano theorem (see [5] ) we obtain for any function the expression on the error

(18)

where and for all n.

Theorem 3. If function, and the derivative has constant sign on interval, then

(19)

if is non-negative on the interval, and

(20)

if is non-positive on the interval.

Proof. Assume that. From the formulas (10) and (18):

because of and and

because of and. □

5. Series Estimation

The sum of a series

(21)

can be approximated by a finite sum. The error of this estimation can be represented as the sum of the series

Therefore, if we have a method of estimating the sum of an infinite series, then this method will enable us to estimate the error of the N-term approximation. One way to estimate the sum of the series is to take into conside- ration the fact that a series can be viewed as an integral over an infinite domain

(22)

for some function for which for all n. Therefore, if for a given series, we know

an explicitly integrable function with this property, then we can take the value of the integral as an estimate for s.

Theorem 4. We assume that the function f is such that

1) f is either positive and decreasing, or negative and increasing.

2) is convergent.

3).

4) is either positive or negative on.

5).

6).

Under this assumptions, if then

(23)

where

If, then we get a similar inequality, but with the right-hand side instead of the left-hand side, and vice versa.

Proof. First, from the inequalities (19) we have:

We can rewrite this inequality in an equivalent form:

(24)

In this inequality we put:, , , so

Because of

than passing with n to in the inequality (24) we obtain

We complete the first part of the proof by adding the term to the both sides of this inequality.

Let. From the inequalities (19) we have:

We rewrite this inequality in an equivalent form:

and put:, , ,. Passing with to we obtain

(25)

because of

We complete the proof by adding the term to the both sides of the inequality (25). □

Acknowledgements

We thank the editor and the referee for their comments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bozek, B., Solak, W. and Szydelko, Z. (2008) A Note on a Family of Quadrature Formulas and Some Applications. Opuscula Mathematica, 28, 109-121.
[2]	Bozek, B., Solak, W. and Szydelko, Z. (2009) A Note of Some Quadrature Rules with Gregory End Corrections. Opuscula Mathematica, 29, 117-129.
[3]	Bozek, B., Solak, W. and Szydelko, Z. (2012) On Some Quadrature Rules with Laplace End Corrections. Central European Journal of Mathematics, 10, 1172-1184. http://dx.doi.org/10.2478/s11533-012-0034-6
[4]	de Villiers, J.M. (1993) A Nodal Spline Interpolant for the Gregory Rule of Even Order. Numerische Mathematik, 66, 123-137. http://dx.doi.org/10.1007/BF01385690
[5]	Kincaid, D. and Cheney, W. (2002) Numerical Analysis, Mathematics of Scientific Computing. 3rd Edition, The University of Texas at Austin, Brooks/Cole-Thomson Learning.