Stochastic Resonance Synergetics—Quantum Information Theory for Multidimensional Scaling ()
1. Introduction
Multidimensional scaling (MDS) refers to a wide variety of methodologies [1] used in expressing, often visualizing [2] , relationships among objects described in a multidimensional space. Two classes of MDS methodologies are used in practice depending on whether a dissimilarity measure is applicable. A metric methodology applies a dissimilarity measure for a data point, while an item-to-item matrix is often used in non-metric methodologies. Both of those classes apply some kind of optimization procedures on a loss function, resulting in a configuration in low dimensional space that capture the most significant relations sought. While a monotonic search in the configuration space often results in a sub-optimal solution, it addresses an issue of computational complexity of exploring configuration spaces for a big database.
Complexity of computation of NP-hard problems has been addressed in the Cerny’s work [3] , and data optimization has been proposed with the simulated annealing procedure [4] . Segmenting joint probability distributions has been recognized as a way to address the issue of computational complexity in NP-hard problems.
Data clustering has been used in various disciplines, like engineering, life and social sciences. The Bayesian inference statistics has been applied in inferring the clustering parameters [5] . The clustering techniques are described as non-parametric optimization procedures where a priori knowledge about the distribution of data is not available.
In life sciences, a synergy hypothesis refers to a natural computation of coordinative structures, and handling biological complexity [6] [7] . We have explored an inherent uncertainty in coordinating shoulder and elbow joints motion, while computing the reaching synergies, in [8] . These results suggest that the motor cortex is con- cerned with a general planning of movement, rather than the details of the load or muscles that will have to be activated to produce a desired end point. We are therefore not searching for a single optimal solution of the movement trajectories, but rather a unique information description of data, referring to different levels of complexity that biological systems control movements, from accurately planned movements to reflexes.
In this work, we propose a unifying approach to the computing and signaling, that ranges across various disciplines, from physics to the behavioral analysis. This quantum information theory lays down, in our view, a new perspective to a networked system dynamics, as well as computation. Dynamic equilibriums, based on bipolar positive-negative synergies [9] , construct a hierarchical map by using the resonance effect. Dimensional exchangeability allows computational methodology that elucidates coordinated structure relations, in the scale- space.
The computational method captures the quantum information theoretical model for the generation of the underlying data. The networked system dynamics and computation is carried out by the scale-space wave information propagation, accompanied by the inherent uncertainty relation in the information expression. Despite its non-linear and dynamical nature, it aims for the simplest description, coding and control of data.
2. Method
A common problem that may occur with an optimization procedure seeking a global minimum is depicted in Figure 1. Various scheduling procedures are proposed [4] [10] in the annealing methods in exploring the scale- space to avoid the solution being trapped in a local minima of a loss function, when moving from the scale β1 to β2.
We address this issue by evaluating a generalized uncertainty relation in a data decomposition. A polynomial data decomposition procedure is derived by computing second order statistics for a system of coupled oscillators, in the hierarchy of scales. A scale equilibrium is evaluated, as shown in Figure 2, for two scale-space waves,
![]()
Figure 1. An effect of a scale change in optimization procedure.
![]() (a) (b)
(a) (b)
Figure 2. Stochastic resonance: scale equilibrium of two coupled waves, F1 and F2. (a) A condition of splitting a cluster, and (b) a condition of the waves resonance within a cluster.
corresponding to the coupled data clusters, F1 and F2. As a result, a binary tree structure of coupled oscillators minimizes synergy exchange among the clusters of data points.
2.1. Variational Data Distribution
We define a cluster of data points by its vector representative y, on a set of data points W, the cluster window of computation. Let d(x, y) denotes a distortion measure of a data point x, induced by the vector representative y. The distortion energy, or variance V of a cluster is defined by:
 (1)
(1)
It can be shown [5] that the probability density function that minimize the entropy:
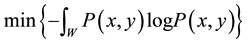 , (2)
, (2)
subject to:
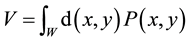
and
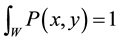 ,
,
is the Gibbs distribution:
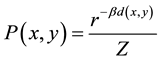 , (3)
, (3)
where
 (4)
(4)
is the partition function on r number of data points within a window W, and β is the Lagrange’s multiplier.
2.2. Covariant Differentiability
A nonlinear dynamics of information segmentation in this work is derived from the model of free energy, originally used in statistical physics to model different complex systems. Along with the variance function V, the free energy F describes the state of r data points cluster, for a given scale parameter β,
 . (5)
. (5)
These functions can be conveniently written within the path integrals in scale β:
 , (6)
, (6)
and
 . (7)
. (7)
We have explored a covariant differentiability in the computational model for a system of coupled oscillators. Here, we show that a scale-space wave information propagation allows motion in the scale-space that conserves information. In this methodology, we refer to the energy and the mass, interchangeably, conveniently using the term information. We therefore, denote this a quantum information theory, and the methodology applied as the scale-space computing.
The constrained equation of motion for the coupled oscillators, exchanging synergies among data clusters, is given by:
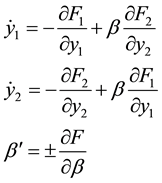 (8)
(8)
This system of equations has the determinant of the map:
 . (9)
. (9)
For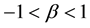 , the Eigen values of the determinant of the map have negative values if for the Hessians of the free energies, F1 and F2, apply:
, the Eigen values of the determinant of the map have negative values if for the Hessians of the free energies, F1 and F2, apply:
 . (10)
. (10)
We refer it as the generalized uncertainty relation. It is used here to assess the condition of numerical stability for the equation of motion, in the coupled system.
This system can be analyzed by the series expansion of the system’s free energies:
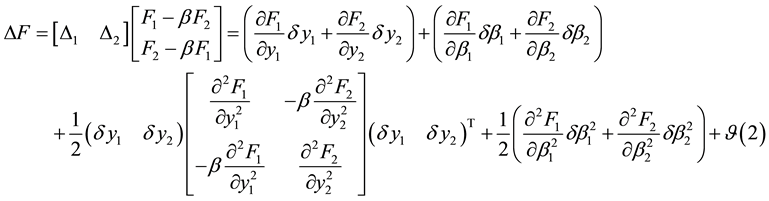 (11)
(11)
Given the covariant differentiability, the methodology is derived for minimizing the synergy exchange in a coupled system of binary oscillators. The update formula for the scale parameter β is given by:
![]() , (12)
, (12)
where
![]() ,
,
and,
![]() , (13)
, (13)
where
![]() .
.
2.3. Stochastic Resonances: Computing Synergies by Scale-Space Wave Information Propagation
The mass conservation principle:
![]() , (14)
, (14)
is accompanied by the scale-space wave information propagation:
![]() . (15)
. (15)
Dynamic equilibriums are computed that conserve information based on bipolar data distributions for two waves, F1 and F2. At the scale equilibrium,
![]() ,
,
the conservation principle can be written as:
![]() . (16)
. (16)
The Green’s function:
![]() ,
,
gives a model of spatial coherency of information for a cluster of data points, at the scale β. The information is distributed into the positive and negative values of the scale-space wave, according to:
![]() (17)
(17)
In the neighborhood of a data point WP, the rotor and divergence orthogonal operators combine to shape the positive and negative envelopes of the scale-space wave. When applied for a high-dimensional signal, the bipolar distribution (17) can be conveniently scaled down along the most singular vectors of the covariance matrices,
![]()
2.4. Algorithm
The main procedure, as written in Figure 3, decomposes data into a binary tree structure. It considers the instance of the whole ensemble of data points. No a priori number of clusters is assumed in the final decomposition.
The generalized uncertainty relation is used to test for the condition of resonance, as shown in Figure 2(b). In
the case of the resonating waves, the information is encapsulated within the nucleon. In the other case, at the saddle point in scale, as shown in Figure 2(a), a phase transition occurs and the cluster is splitted in two, complying to the information conservation rule, written in (17). We denote the final decomposition―an atom, bind- ing a finite number of nucleons of information.
The system of coupled oscillators is brought to an equilibrium in scale by the procedure, as written in Figure 4. The covariance differentiability allows the coupled clusters exchanging synergies, according to (12) and (13). The conservation principle shapes the data waves with the Green function G(β,y), following the rule (17).
3. Results
In this section, we assess the key properties of our methodology by showing data distributions in different applications. The level for resonance, in Algorithm 1, is set such that in all the applications shown, data decomposition falls within a single nucleon information. The four color code (red, blue, green, yellow) is used to code the positive/negative envelopes of the two scale-space waves (red/yellow and blue/green) that are being brought into the resonance, within a nucleon.
3.1. Two-Dimensional Data Scatter
An example of data scaling is shown in Figure 5 for two-dimensional Gaussians displaced at different locations. Three Gaussians, each with 30 data points, dispersed with σ = 1 are displaced along X, Y coordinates at the displacement intervals d = 2 - 7. The scatter plot at Figure 5(a) is shown for the displacement d = 5. A unique statistical description is generated by equilibrating the two scale-space data waves into the resonance. The scale parameter at the equilibrium, in this experiment, follows a monotonic distance relation to the displacement parameters, resulting in β(2) = +0.000225, β(3) = +0.000124, β(4) = +0.000029, β(5)= +0.000013, β(6) = −0.000129, β(7) = −0.000365, at the displacements d = 2 - 7, respectively.
In all of the plots of Figures 5(b)-(g), the “upper” Gaussians are shaped by the opposing envelopes (yellow and green) of the two scale-space waves, forming the nucleons. The other two Gaussians are mostly shaped by the single envelopes (red and blue) of the two scale-space waves.
3.2. Image Motion
Sequences of two images are used in assessing image motion computed by the stochastic resonance. We use the optical flow equation [11] for the distortion measure, applying to a cluster of data points:
![]() ,
,
where ![]() and
and ![]() are the sequence and spatial derivatives at a data point, and
are the sequence and spatial derivatives at a data point, and ![]() is the group velocity of the information flow for a cluster of data points. The 4 neighboring pixels stencil WP is used in applying the local operators in (17), the divergence and rotor.
is the group velocity of the information flow for a cluster of data points. The 4 neighboring pixels stencil WP is used in applying the local operators in (17), the divergence and rotor.
The “ball” image, I1 in Figure 6(a), is radially expanded, I2 in Figure 6(b), and moved toward down-right corner, I3 in Figure 6(c). The quantum information of the image motion is decomposed within a nucleon, for the
![]()
Figure 4. Scale equilibrate two waves, F1 and F2.
![]()
Figure 5. Two-dimensional data scatter decomposition. (a) Three Gaussians with the data dispersion σ = 1, at distance d = 5. Varying distance d, data decompose within a nucleon at different scales β: (b) β(2) = +0.000225, (c) β(3) = +0.000124, (d) β(4) = +0.000029, (e) β(5) = +0.000013, (f) β(6) = −0.000129, and (g) β(7) = −0.000365.
motion sequences, I1 → I2 in Figure 6(d), I2 → I3 in Figure 6(e), and I1 → I3 in Figure 6(f). All three decompositions result in a single nucleon for a chosen level of signal resonance, at β = 0.13444 in (d), β = 0.18127 in (e), and β = 0.14785 in (f).
3.3. Neuroimaging
The dynamical data modeling enables a synchronicity measure for the brain wave signals, as we show in the EEG scan. Multidimensional signal scaling in neuroimaging is shown useful also in functional mapping of the neuroanatomy, by the fMRI signal scan analysis. In both of these applications, the information is decomposed within nucleons; in the first by employing the temporal synergy exchange, while in the second, the spatial.
3.3.1. EEG: The Brainwave Nucleons
Two channels EEG recording, shown in Figure 7(a) and Figure 7(b), totaling N = 83400 data points are obtained during a sleep, [12] . The signal is decomposed by two scale-space waves brought into the scale equilibrium, at β = 0.4. They resonate the information within a nucleon by exchanging temporal synergies. The resulting two-channels signal decomposition is showed in Figure 7(c) and Figure 7(d).
3.3.2. fMRI: The Neuronal Representation of Sound Distance in Human Auditory Cortex
Experiments were performed in [13] to infer the neuronal representations of sound distance in human auditory
![]()
![]() (a) Ch. 1recording (b) Ch. 2 recording
(a) Ch. 1recording (b) Ch. 2 recording![]() (c) Ch. 1 decomposition (d) Ch. 2 decomposition
(c) Ch. 1 decomposition (d) Ch. 2 decomposition
Figure 7. EEG neuroimaging. (a) (b) 2 channels recording during a sleep; (c) (d) Signal decomposition within the nucleon, at β = 0.4.
cortex, and the fMRI brain scans were obtained for two behaviorally correlated sound distance perception conditions. The BOLD signal level difference in the brain scans for these two conditions reveal an area in the human auditory cortex particularly active in processing the sound distance, independent of the sound intensity.
In this work, we compute a coupling structure of the information flow for the two stimulus conditions. The scale-space wave information propagation segments the brain activation regions that resonate the information by the spatial exchange of synergies. The term information flow better explains the results obtained, since neither temporal continuity in the fMRI sequences is assumed, nor the order of the images in a sequence.
In Figures 8(g)-(h), two waves are shown with the four segments, the red and green in the L, and the blue and yellow in the R. They are brought into resonatating the information flow between the correlated signal activations: L1 & R1 vs. L2 & R2, shown in Figures 8(a)-(d). Due to a more coherent flow in the R stream, the blue/yellow wave is opposed to the more structured, the red/green in the L. This information decomposition is brought into the resonance at β = 0.010128.
Two distinct patterns can be observed in the red segment: 1) the stripe-like pattern, going more orthogonally
from the main activation area for the sound distance perception, as reported in [13] and shown in Figure 8(e), and 2) the blob-like pattern, going more laterally from the main activation area. These repetitive patterns show comparably the same spatial frequency in the signal.
4. Discussion
The coupled structure of binding synergies functionally conceptualize the information content, in time, as discussed in the EEG example, or in space, as described with the spatial distribution of the fMRI signals. We denote it the genotype signal analysis that elucidates our understanding of the Space-Time relations, dynamics, and evolution. When describing a multidimensional data decomposition, scaled along one-dimensional path in space, a principle of “least action” is constructed out of minimizing the synergy exchange. Generally, chaotic cycles result out of the scale-space network statistics. Their control is a challenging research, in our view, which opens up a new perspective, from subatomic to diseases treatment and regenerative medicine. We envision it therefore as a unifying approach to signaling and computing, that ranges across various disciplines, from quantum physics to a behavioral analysis.
We have tested this algorithm in different applications. Two dimensional data scatter, in Figure 5, shows an example of data binding by minimizing the synergy exchange, by our methodology. A unique statistical description of data is obtained, that gives a solution to connecting two-dimensional data along one-dimensional minimal-distance path. As a distance d between three Gaussian data clusters increases, the uncertainty in connecting them in a minimal-distance path decreases. Progressively smaller number of the between clusters binding points can be observed in the data decompositions, in Figures 5(b)-(g).
The scale parameter at the equilibrium, in this experiment, follows a monotonic distance relation to the displacement parameters. We propose this monotonic relation also to be used in assessing the synchronicity level of the brain wave pattern, that is shown in Figures 7(c)-(d).
Higher amplitudes and temporal frequencies can be observed in red and blue envelopes of the scale-space waves, as opposed to the green and yellow envelopes. The highest frequencies in the signal, that correspond to the REM phases of the sleep, have effectively been shut down in the yellow components, to a zero level. When taken as a whole, this indicates that the scale-space decomposition exchange temporal synergies sensitive to the local content of temporal frequencies. Two resonating waves balance the information content in the brain waves with components distributed distinctively in the time-frequency bands.
The fMRI neuroimaging application is accompanied in this work by the results of two-dimensional image motion computation, in the examples shown in Figure 6. In the radial motion expansion, I1 → I2, the nucleon of the image motion decomposition, shown in Figure 6(d), form the radially symmetric dynamical map along the image diagonals. This distribution can be described also as the maximally entropic, given that any other 4-seg- ments image motion distribution would be a more biased estimate of the image motion. For an example, the 4-segments paralleling the square edges would give a less separable image motion distributions, due to the smaller image gradients at the center of the image compared to the corners. In Figure 6(e), the down-right motion is distinctively coded by the green-blue wave pattern along the image motion diagonal. The largest image motion energy is fine coded by the red-green pattern in the down-right quadrant of the image, in Figure 6(f).
The point scaling property of the information flow is analyzed in the fMRI images. Two experiments were conducted [13] in the approach to study intensity independent sound distance processing, by the auditory cortex. One with varying distance, and one with varying intensity of the sound. The fMRI BOLD signal recordings from a passive listener are shown in Figures 8(a)-(d), respectively. An area of the strongest activation, conveniently denoted as the feature detector in the sound distance perception is found by differentiating signal activations for those two conditions, and shown in Figure 8(e) and Figure 8(f).
We extend this analysis showing the information flow point scaling effect in Figures 8(g) and Figure 8(h). The information flow within the activation area in L, shown in the red segment in Figure 8(g), is of the particular importance. Distinct pattern of the scaling property of information can be observed from the flow going to a still, at the point of the feature detector. The stripe-like pattern, originating on the top part of the activation area is followed down by the blob-like pattern with the same lateral extension. In our view, it conforms to the tonotopic map of the “where” stream in the auditory information flow [14] . This component of the information flow is brought to a still with the two additional blobs projecting further down toward the area of the feature detector, shown in Figure 8(e).
5. Conclusions
The theory of stochastic resonance synergies is derived and a new data modeling methodology is described for multidimensional signals scaling. We have proposed it within a quantum information theory [15] that lays down a new perspective to networked systems dynamics [16] and computation. Unique statistical description of data are obtained via dynamical cascades, using the resonance effect. We intend to use this theory in behavioral data analysis and neuroimaging of the binding structures, extracted from the EEG/fMRI scans in the dynamical feature maps.
Coding and control structures in data have been explored by our methodology for the analysis purposes and data mining. Computing and control by parallel computer architectures have been also studied in [17] . The scalable coding gives a way, in our view, for the progressive data transmission, and the storage of large databases. The polynomial complexity in the computing scheme, also, allows a relative independence from a current state of the technology used.
Acknowledgements
This work was supported in part by the Slovak National Stipends (SAIA) Program. I am grateful to Norbert Kopco for providing the fMRI data and useful comments while writing this manuscript.