Equivalence of K-Functionals and Modulus of Smoothness Generated by a Generalized Dunkl Operator on the Real Line

Reem Fahad Al Subaie¹, Mohamed Ali Mourou^2*

¹Department of Mathematics, College of Sciences for Girls, University of Dammam, Dammam, Kingdom of Saudi Arabia.
²Department of Mathematics, Faculty of Sciences of Monastir, University of Monastir, Monastir, Tunisia.

DOI: 10.4236/apm.2015.56035                

Abstract

This paper is intended to establish the equivalence between K-functionals and modulus of smoothness tied to a Dunkl type operator on the real line.

Keywords

Differential-Difference Operator, Generalized Fourier Transform, Generalized Translation Operators, K-Functionals, Modulus of Smoothness

1. Introduction

Consider the first-order singular differential-difference operator on the real line

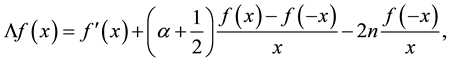
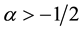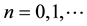where and. For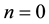, we regain the differential-difference operator

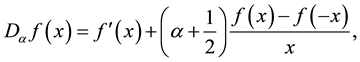
which is referred to as the Dunkl operator with parameter 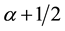associated with the reflection group 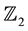on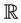. Such operators have been introduced by Dunkl [1] -[3] in connection with a generalization of the classical theory of spherical harmonics. The one-dimensional Dunkl operator plays a major role in the study of quantum harmonic oscillators governed by Wigner’s commutation rules [4] -[6] .

The authors have developed in [7] [8] a new harmonic analysis on the real line related to the differential-dif- ference operator 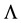in which several classical analytic structures such as the Fourier transform, the translation operators, the convolution product, ..., were generalized. With the help of the translation operators tied to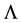, we construct in this paper generalized modulus of smoothness in the Hilbert space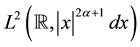. Next, we define Sobolev type spaces and K-functionals generated by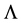. Using essentially the properties of the Fourier transform associated to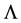, we establish the equivalence between K-functionals and modulus of smoothness.

In the classical theory of approximation of functions on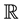, the modulus of smoothness are basically built by means of the translation operators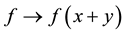. As the notion of translation operators was extended to various contexts (see [9] [10] and the references therein), many generalized modulus of smoothness have been discovered. Such generalized modulus of smoothness are often more convenient than the usual ones for the study of the connection between the smoothness properties of a function and the best approximations of this function in weight functional spaces (see [11] -[13] and references therein).

In addition to modulus of smoothness, the K-functionals introduced by J. Peetre [14] have turned out to be a simple and efficient tool for the description of smoothness properties of functions. The study of the connection between these two quantities is one of the main problems in the theory of approximation of functions. In the classical setting, the equivalence of modulus of smoothness and K-functionals has been established in [15] . For various generalized modulus of smoothness these problems are studied, for example, in [16] -[19] . It is pointed out that the results obtained in [16] emerge as easy consequences of those stated in the present paper by simply taking.

2. Preliminaries

In this section, we develop some results from harmonic analysis related to the differential-difference operator. Further details can be found in [7] [8] . In all what follows assume and n a non-negative integer.

The one-dimensional Dunkl kernel is defined by

(1)

where

is the normalized spherical Bessel function of index. It is well-known that the functions, , are solutions of the differential-difference equation

(2)

Furthermore, we have the Laplace type integral representations:

(3)

(4)

where

(5)

The following properties will be useful for the sequel.

Lemma 1 1) For all,.

2) There is such that for all with.

3) For all,.

4) For all,

Proof. Assertions (1) and (2) are proved in [16] . By (1), (4) and the fact that

we have

Clearly the integral above is null only for, which proves assertion (3). Let us check assertion (4). Using (3) and the fact that

(6)

we get

By (6),

Moreover,

which concludes the proof.

Notation 1 Put

We denote by

Ÿ the class of measurable functions f on for which

Ÿ the space of functions f on, which are rapidly decreasing together with their derivatives, i.e., such that for all,

The topology of is defined by the semi-norms,.

Ÿ the subspace of consisting of functions f such that

Ÿ the space of tempered distributions on.

Ÿ the topological dual of.

Clearly is a linear bounded operator from into itself. Accordingly, if define by

For and, let be defined by

Definition 1 The generalized Fourier transform of a function is defined by

Remark 1 If then reduces to the Dunkl transform with parameter associated with the reflection group on (see [3] ).

Theorem 1 The generalized Fourier transform is a topological isomorphism from onto. The inverse transform is given by

where

Theorem 2 1) For every we have the Plancherel formula

2) The generalized Fourier transform extends uniquely to an isometric isomorphism from onto.

Definition 2 The generalized Fourier transform of a distribution is defined by

Theorem 3 The generalized Fourier transform is one-to-one from onto.

Lemma 2 If then the functional

is a tempered distribution. Moreover,

(7)

with.

Proof. The fact that follows readily by Schwarz inequality. Let. It is easily checked that

where. So using Theorem 2 we get

which completes the proof.

Lemma 3 Let and. Then for we have

(8)

(9)

Proof. Identity (8) may be found in [7] . If then

But by (8),

So

which ends the proof.

Notation 2 From now on assume. Let be the Sobolev type space constructed by the dif- ferential-difference operator, i.e.,

More explicitly, if and only if for each, there is a function in abusively denoted by, such that.

Proposition 1 For we have

(10)

Proof. From the definition of we have

By (7) and (9),

with. Again by (7),

with. Identity (10) is now immediate.

Definition 3 The generalized translation operators, , tied to are defined by

where

with given by (5).

Proposition 2 Let and. Then and

(11)

Furthermore,

(12)

3. Equivalence of K-Functionals and Modulus of Smoothness

Definition 4 Let and. Then

Ÿ The generalized modulus of smoothness is defined by

where

I being the unit operator.

Ÿ The generalized K-functional is defined by

The next theorem, which is the main result of this paper, establishes the equivalence between the generalized modulus of smoothness and the generalized K-functional:

Theorem 4 There are two positive constants and such that

for all and.

In order to prove Theorem 4, we shall need some preliminary results.

Lemma 4 Let and. Then

(13)

(14)

Proof. The result follows easily by using (11), (12) and an induction on m.

Lemma 5 For all and we have

(15)

Proof. By (10), (14), Lemma 1 (4) and Theorem 2 we have

which is the desired result.

Notation 3 For and define the function

Proposition 3 Let and. Then

1) The function is infinitely differentiable on and

(16)

for all.

2) For all, and

(17)

where

Proof. The fact that follows from the derivation theorem under the integral sign. Identity (16) follows readily from (2) and the relationship

which is proved in [7] . Assertion (2) is a consequence of (16) and Theorem 2.

Lemma 6 There is a positive constant such that

for any and.

Proof. By (17) and Theorem 2, we have

By Lemma 1 (2) there is a constant which depends only on and n such that

for all with. From this, (14) and Theorem 2 we get

which achieves the proof.

Corollary 1 For all and we have

where c is as in Lemma 6.

Lemma 7 There is a positive constant such that

for every and.

Proof. By (17) and Theorem 2 we have

Put

By L’Hôpital’s rule,

This when combined with Lemma 1 (3) entails. Moreover,

Therefore

by virtue of (14) and Theorem 2.

Corollary 2 For any and we have

where C is as in Lemma 7.

Proof of Theorem 4. 1) Let and. By (13) and (15), we have

Calculating the supremum with respect to and the infimum with respect to all possible functions we obtain

with.

2) Let be a positive real number. As it follows from the definition of the K-functional and Corollaries 1 and 2 that

Since is arbitrary, by choosing we get

with. This concludes the proof.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dunkl, C.F. (1989) Differential-Difference Operators Associated to Reflection Groups. Transactions of the American Mathematical Society, 311, 167-183. http://dx.doi.org/10.1090/S0002-9947-1989-0951883-8
[2]	Dunkl, C.F. (1991) Integral Kernels with Reflection Group Invariance. Canadian Journal of Mathematics, 43, 1213-1227. http://dx.doi.org/10.4153/CJM-1991-069-8
[3]	Dunkl, C.F. (1992) Hankel Transforms Associated to Finite Reflection Groups. Contemporary Mathematics, 138, 128-138. http://dx.doi.org/10.1090/conm/138/1199124
[4]	Kamefuchi, S. and Ohnuki, Y. (1982) Quantum Field Theory and Parastatistics. University of Tokyo Press, Springer-Verlag, Tokyo, Berlin.
[5]	Rosenblum, M. (1994) Generalized Hermite Polynomials and the Bose-Like Oscillator Calculus. Operator Theory: Advances and Applications, 73, 369-396. http://dx.doi.org/10.1007/978-3-0348-8522-5_15
[6]	Yang, L.M. (1951) A Note on the Quantum Rule of the Harmonic Oscillator. Physical Review Letters, 84, 788-790. http://dx.doi.org/10.1103/PhysRev.84.788
[7]	Al Sadhan, S.A., Al Subaie, R.F. and Mourou, M.A. (2014) Harmonic Analysis Associated with A First-Order Singular Differential-Difference Operator on the Real Line. Current Advances in Mathematics Research, 1, 23-34.
[8]	Al Subaie, R.F. and Mourou, M.A. (2014) Inversion of Two Dunkl Type Intertwining Operators on R Using Generalized Wavelets. Far East Journal of Applied Mathematics, 88, 91-120.
[9]	Mourou, M.A. and Trimèche, K. (2003) Transmutation Operators and Paley-Wiener Theorem Associated with a Singular Differential-Difference Operator on the Real Line. Analysis and Applications, 1, 43-69. http://dx.doi.org/10.1142/S0219530503000090
[10]	Trimèche, K. (1981) Transformation intégrale de Weyl et théorème de Paley-Wiener associés à un opérateur différentiel singulier sur . Journal de Mathématiques Pures et Appliquées, 60, 51-98.
[11]	Platonov, S.S. (2000) Generalized Bessel Translations and Certain Problems of the Theory of Approximation of Functions in the Metrics of L2,α. I. Trudy Petrozavodskogo Gosudarstvennogo Universiteta, Seriya Matematika, 7, 70-82.
[12]	Platonov, S.S. (2001) Generalized Bessel Translations and Certain Problems of the Theory of Approximation of Functions in the Metrics of L2,α. II. Trudy Petrozavodskogo Gosudarstvennogo Universiteta, Seriya Matematika, 8, 1-17.
[13]	Potapov, M.K. (1998) Application of the Operator of Generalized Translation in Approximation Theory. Vestnik Moskovskogo Universiteta, Seriya Matematika, Mekhanika, 3, 38-48.
[14]	Peetre, J. (1963) A Theory of Interpolation of Normed Spaces. Notes de Universidade de Brasilia, Brasilia.
[15]	Berens, H. and Buter, P.L. (1967) Semi-Groups of Operators and Approximation. Grundlehren der mathematischen Wissenschaften, 145, Springer, Berlin.
[16]	Belkina, E.S. and Platonov, S.S. (2008) Equivalence of K-Functionnals and Modulus of Smoothness Constructed by Generalized Dunkl Translations. Izvestiya Vysshikh Uchebnykh Zavedenii Matematika, 8, 3-15.
[17]	Dai, F. (2003) Some Equivalence Theorems with K-Functionals. Journal of Approximation Theory, 121, 143-157. http://dx.doi.org/10.1016/S0021-9045(02)00059-X
[18]	Ditzian, Z. and Totik, V. (1987) Moduli of Smoothness. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-4778-4
[19]	L?fstróm, J. and Peetre, J. (1969) Approximation Theorems Connected with Generalized Translations. Mathematische Annalen, 181, 255-268. http://dx.doi.org/10.1007/BF01350664