Performance Evaluation of One-Way Concrete Slabs Reinforced with New Developed GFRP Bars ()
1. Introduction
Durability of reinforced concrete (RC) structures is one of the most important points to be considered. In many cases steel RC structures are subjected to corrosive environments. In aggressive environments, the use of steel reinforcing bars stands out as a significant factor leading to significant limit of the life expectancy of reinforced concrete structures. The use of fiber reinforced polymers (FRP) reinforcement is particularly attractive for structures that operate in aggressive environments, such as in coastal regions. The magnetic transparency of FRP bars makes it a unique material that can be used to reinforce buildings that host magnetic resonance imaging (MRI) units or other equipments sensitive to electromagnetic fields. FRP composite bars in general offer many advantages over conventional steel, including one-quarter to one-fifth the density of steel, high fatigue resistance, no corrosion even in harsh chemical environments, greater tensile strength than steel, and ease of handling at job sites and cutting [1] -[4] . In recent years, the progressive development in FRP mechanical and physical properties has promoted the use of FRP as internal reinforcement in RC structural members. Because of the difference in mechanical and physical properties of FRP bars compared with steel bars, especially regarding the surface deformation and the modulus of elasticity, the bond behavior of FRP reinforced concrete specimens is quite different than that of steel reinforced specimens [5] -[7] . Whereas, the mechanical properties of the FRP bars are one of the main aspects to be considered in the design of concrete structures. Enhancing the bond of reinforcing bars is considered an efficient technique to improve the load-carrying capacity of such concrete element. Also, crack width deformability, and strength, of concrete are significantly enhanced by increasing the bond strength between concrete and FRP bars. Based on the existing experience of bond behavior of FRP bars in concrete, the primary variables which influence the bond strength are: bar type, bar diameter, shape of cross section, surface characteristics, embedment length, strength and cover of bonding agent, and temperature [8] . Although, extensive studies were conducted to study concrete flexural elements reinforced with circular cross-section FRP bars [3] [6] [7] [9] -[12] , up to date, there is a scarcity of data available from effect of bar shape, particularly square cross- section. In this paper, the behavior of RC slab reinforced with newly develop GFRP square cross-section bar conducted to provide additional understanding regarding the serviceability and flexural behavior as a result of change of bond properties using GFRP square bars.
2. Research Significance
GFRP bars with square and circular cross sections are fabricated in the lab. The study presents stages of fabrication of the FRP bars as well as their mechanical and physical properties. The effect of using those bars was examined through testing the behavior of one way slabs with different concrete types. Therefore, better understanding to the effect of test parameters on improving the bond that resulted in the enhancement of the slab general behavior. The physical and mechanical characteristics of GFRP bars, considered fiber content of GFRP-bars, unit weight of the GFRP-bars, and tensile strength and modulus of elasticity of GFRP-bars with square and circular cross section area.
3. Characterization of Physical Properties of GFRP Bars
3.1. Fiber Content of GFRP Bars (F%)
Fifteen 30 mm long samples of square GFRP bars were prepared and tested according to ASTM E1131 [13] to determine the fiber content (F%) with different number of yarns (80, 100, 130, and 144 yarns) to achieve a minimum requirement of CSA S-807-10 [14] , and ACI 440.6M-08 [15] (70% fiber content by weight or 55% as fiber content by volume). The samples were accurately weighed and heated at 600˚C for 5 hours. The weight loss was recorded as a function of temperature. The weight loss at 600˚C was measured. The fiber content by weight (F%) was then calculated according to the following equation:
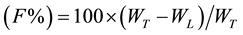 (1)
(1)
where,
F% = fiber content;
WL = weight loss at 600˚C;
WT = total weight of FRP sample.
3.2. Unit Weight of GFRP Bars
The unit weight of the bars is an important parameter for comparing between the GFRP bars (square and circular cross section) and steel bars as reinforcement for the structural elements. The unit weight of the bars given an indication of strength to weight of the GFRP bar. The unit weight (γ) of the GFRP bars was determined by the following equation:
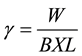 (2)
(2)
where,
W = Total weight of square GFRP sample;
B = Dimension of square GFRP-bar;
L = Measured length of square GFRP sample.
3.3. Tensile Test of GFRP Bars
All square GFRP-bars of 14.1 × 14.1 mm and circular GFRP-bars 16 mm diameter specimens were tested under tension according to ASTM D7205. The GFRP specimen length as well as the length and diameter of the anchor to be used for the tensile test were calculated according to ASTM D7205 [15] . Figure 1 shows the dimensions of test specimens. The tests were carried out using the Baldwin testing machine in the structures laboratory of the Department of Civil Engineering at the Helwan University. The test specimens were instrumented with one linear variable differential transformer (LVDT) with 200 mm measured length to capture specimen elongation during testing. For each tensile test, the specimen was mounted on the press with the steel pipe anchors gripped by the wedges of the upper and the lower jaw of the machine. All specimens were tested until failure with average rate of loading ranging between 47.5 KN/min. The applied load and bar elongation was recorded during the test with a computer data-acquisition system. Due to the brittle nature of FRP, no yielding occurred and the stress-strain behavior remained linear till failure.
4. Experimental Program
4.1. GFRP Bars Fabrication and Material Properties
GFRP square (14.1 × 14.1 mm) and circular (16 mm diameter) cross-sections reinforcing bars were fabricated in the lab by mechanical pultrusion process. The pultrusion is a common technique for manufacturing continuous lengths of FRP bars of constant profile. As illustrated in Figure 2, Continuous strands of reinforcing material are drawn from creels, through a thermosetting vinylester resin tank. The fiber stands becomes fully impregnated with the resin such that all the fiber filaments are thoroughly saturated with the resin mixture. Once the resin impregnated fiber filaments, the un-cured composite material was passed through the mouth of two-part heated die with circular or square hole (see Figure 2) to arrange and organize the fiber into the correct shape (circular or square), while excess resin is squeezed out. The speed of pulling through the die is predetermined by the curing time needed. At the end of this pultrusion machine was a cut-off by mechanical saw to get the required of length. After manufacturing the bars, the corners of square bars were rounded with small curvature to prevent stress concentration, to avoid initiation internal cracks between the bar and concrete.
To ensure good bond with concrete, the surface of the bars was braided by fiber yarns by a pitch of 10 mm. The properties of the final product of the bar are shown in Table 1.
Slab specimens were constructed using normal weight concrete mix. Polypropylene fibers were used in the concrete mix with a variable average compressive strength as 25, 35, and 45 MPa. The concrete compressive strength was determined from the average test results of 10 concrete cylinders (150 × 300 mm) at the same day of slabs tests.
![]()
Figure 1. Tensile test dimension of tested square GFRP-bar.
![]()
Figure 2. Pultrusion process: (a) Schematic showing the process of pultrusion of GFRP-square bars; (b) Creel of fiber; (c) Resin tank; (d) Heated die; and (e) Pullers machine.
![]()
Table 1. Mechanical properties of reinforcing bars.
4.2. Test Matrix and Specimen Preparation
A total of nine full-size one way slabs reinforced with GFRP and steel bars were constructed and tested up to failure. The slabs measured 2100 mm long, 500 mm wide, and 140 mm depth. Figure 3 shows the dimensions, different configurations, and reinforcement details of the test specimens. The slabs were reinforced in both directions with a clear concrete cover of 15 mm. The test parameters were the type of reinforcing bars (GFRP versus steel bars), the reinforcement ratio ρf [0.857% (3 bars), 1.142% (4 bars), and 1.428% (5 bars)], bar cross section shape (square or circular), concrete compressive strength (25, 35, and 45 MPa), and polypropylene fiber ratio [0%, 1.5% (14.7 N/m3) , and 2.5% (24.5 N/m3)] which were added to the concrete mix.
Table 2 provides the test matrix and reinforcement details of the slab specimens. Each specimen is identified with two letters and three numbers. The first letter S or G identify specimens as being reinforced with steel or GFRP bars, respectively. While, second letter C or S referring to cross section of the bars as circular or square, respectively. On the other hand, the first number in the specimen identification indicates the number of longitudinal steel or GFRP bars. The second and third numbers stands for the concrete compressive strength and polypropylene fiber ratio, respectively. The specimens were divided into five groups as indicated in the test matrix as reported in Table 2. Group I includes one control RC steel specimen (S-3C-25-0). The specimen was reinforced longitudinally with 3 M15 steel bars as reference for comparison with GFRP RC slabs. Group II includes two specimens to study the effect of cross section shape of GFRP longitudinal bars (G-3C-25-1.5, and G-3S-25-1.5). The two specimens were reinforced longitudinally with 3 GFRP bars (16 mm of diameter for circular; 14.1 × 14.1 mm for square) have identical longitudinal reinforcement stiffness. Group III includes two specimens, which served to study the effect of concrete compressive strength on the ultimate capacity of RC slabs reinforced with square-GFRP bars (G-3S-35-1.5; G-3S-45-1.5). The specimens in this group were reinforced longitudinally with 3 square-GFRP bars and the concrete compressive strengths were 35 and 45 MPa. Group IV included two specimens (G-4S-25-1.5, G8V G-5S-25-1.5) to study the effect of reinforcement ratio with two different ratios of square-GFRP bars (4 and 5 square GFRP bars, respectively). Finally, Group V included two specimens (G-3S-25-0; G-3S-25-2.5) to study the effect of adding polypropylene fiber. Specimen G-3S-25-1.5 (Group II) served as a reference for group III, IV, and V. P.P = polypropylene fiber, ρf = reinforcement ratio of
![]()
Figure 3. Configuration, reinforcement details, and dimensions of the RC slabs.
![]()
Table 2. Details of slabs specimens.
*In first letter, S and G denote the longitudinal reinforcement type (Steel versus glass FRP). In second letter, C and S denote the cross section of the bars (C = circular bar, S = square bar).
longitudinal reinforcement.
GFRP and steel cages were assembled for the slab specimens, as shown in Figure 4. Wooden formworks were constructed for casting the specimens. The concrete was discharged into the slab forms; an electric internal vibrator was used to consolidate the concrete and to remove air bubbles. Figure 4 illustrates the fabrication process of the slab specimens before and after casting. One day after casting, the water was sprayed three times per day for concrete curing, the curing process was maintained for one week.
4.3. Test Setup and Instrumentation
All slabs were tested under four-point bending over a clear span of 1950 mm and a shear span of 650 mm, as shown in Figure 5. A hydraulic jack was used to apply a concentrated load on a steel distribution I-beam to produce two-point loading condition. Three LVDTs were used for each specimen to monitor the vertical displacements; one LVDT was located at mid-span, two LVDTs were located at quarter-span. For each specimen, three strain gages were attached to GFRP reinforcement at mid-span and quarter-points to monitor the bar strain during loading. Also, two external strain gages were attached directly to the concrete surface at mid-span to measure the maximum compressive strains in concrete (see Figure 5). The load was statically applied at a stroke-controlled rate of 1.2 mm/min. During loading, crack formation on both slab sides were marked and crack widths measured.
5. Test Results and Discussion
In this study, the test results are presented in terms of the physical and mechanical properties of GFRP bars of square and circular cross sections. In addition, the results of cracking, deflections, strains in reinforcing bars and concrete, ultimate capacity and modes of failure in RC one-way slabs reinforced with GFRP and steel bars are presented.
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 4. Fabrication process of the slab specimens: (a) Overview of the of the assembled GFRP cages; (b) GFRP cage inside the formwork; (c) Slab specimens after casting.
5.1. Physical Properties of GFRP Bars
The test results indicated that the glass-fiber content by weight for square-GFRP bars and circular-GFRP bars with the same number of yarns were 72.19% and 71.57%, respectively which is accepted according to [14] and [15] . The test result also showed that the unit weight of square GFRP bars ranged from 15.69 to 25.6 KN/m3 according to the number of yarns which were used between 80 and 144 yarns per bar. Table 3 provides the average values of the fiber content and unit weight of square and circular-GFRP bars with different number of fiber yarns per bar.
![]()
Figure 5. Dimensions of the RC slabs, test setup, and instrumentation.
![]()
Table 3. Physical properties of GFRP reinforcing bars.
5.2. Tensile Test of GFRP-Bars
Figure 6 shows the stress-strain relationships of the square and circular GFRP bars. It can be seen that no yielding occurred. The stress-strain behavior was linear as expected. The tensile strength, elastic tensile modulus, and ultimate strain of square-GFRP bars are 642 MPa, 47.5 GPa, and 1.36%, respectively. Moreover, the tensile strength, elastic tensile modulus, and ultimate strain of circular-GFRP bars are 630 MPa, 45.1 GPa, and 1.42%, respectively, as reported in Table 1.
5.3. Load-Deflection Response
Table 4 represents the test results for the test specimens. Also, Figures 7-10 show the mid-span deflection versus applied loads for the tested slabs and the effect of variable parameters considered in this study (reinforcement type and reinforcement ratio; cross section shape; concrete compressive strength; polypropylene fiber ratio). For all tested slabs, the load-deflection relationship was a nearly bilinear response up to failure. The specimens had approximately a similar stiffness up to the initiation of the first crack, followed by a reduction in the stiffness for all slabs but with different tendencies. After cracking stage, the stiffness of tested slabs was dependent on the axial stiffness of the reinforcing bars EfAf.
Figure 7 shows that, the specimen reinforced with steel bars (S-3C-25-0) exhibited more postcracking flexure stiffness and less deflection compared with the slabs reinforced with GFRP bars (G-3C-25-1.5; G-3S-25-1.5). On other hand, the change of the cross section shape of the GFRP bars between the slab reinforced with GFRP- square bars (G-3S-25-1.5) and the slab reinforced with GFRP-circular bars (G-3C-25-1.5) resulted in increasing
![]()
Figure 6. Stress-strain relationship of GFRP-square and circular cross section bars.
a) Yielding of the steel followed by crushing of concrete, b) Crushing of concrete followed by the rupture.
![]()
Figure 7. Effect of reinforcement type and bar cross section shape.
![]()
Figure 8. Effect of concrete compressive strength.
![]()
Figure 9. Effect of reinforcement ratio.
![]()
Figure 10. Effect of polypropylene fiber ratio.
the surface area of GFRP-bars by about 12% at the same cross section area. This increase appeared as a difference in the load deflection relationship. As a result, increasing the surface area of the bars improved the bond between these bars with concrete, and consequently increased the stiffness and decreased the deflection of slab (G-3S-25-1.5) up to failure.
Figure 8 shows the effect of the concrete compressive strength on the deflection behavior of the slabs reinforced with GFRP-square bars. It can be seen that, the slab (G-3S-45-1.5) with the concrete strength of 45 MPa had improved concrete mechanical properties consequently, increased stiffness and decreased deflection compared to the slabs of 35 MPa (G-3S-35-1.5), and 25 MPa (G-3S-25-1.5) at the same load level.
Figure 9 shows that the higher reinforcement ratio for the slab reinforced with 5 GFRP-square bars (G- 5S-25-1.5) resulted in higher stiffness and less deflection compared to slabs reinforced with 4 GFRP-square bars (G-4S-25-1.5) and 3 GFRP-square bars (G-3S-25-1.5).
Adding polypropylene fibers to concrete in known to enhance the concrete microcracking and consequently the concrete tensile strength. Figure 10 represents the effect of amount of the polypropylene fibers which was added to the concrete mix. Increasing the polypropylene fibers in the concrete mix improved the tensile strength of concrete, resulting in the appearance of the first crack appeared at higher load level and delaying the stiffness reduction to a higher level of loading. Also, after reaching the cracking load, the stiffness of postcracked zone depended on the amount of the polypropylene fibers added to the concrete mix, the higher amount of the polypropylene fibers resulted in a higher stiffness. This improvement was proportional to the amount of the polypropylene fibers. This was very obvious with the slab (G-3S-25-2.5) having amount of 24.5 N/m3 of the polypropylene fibers in its mix which had the minimum deflections and maximum stiffness compared to the corresponding slab (G-3S-25-0) without polypropylene fibers in its concrete mix.
5.4. Cracking and Ultimate Load
For all tested slabs reinforced with GFRP-bars, the relationship between the cracking and ultimate loads versus different parameters (type of reinforcement bars, cross sectional shape of the bars, concrete compressive strength, reinforcement ratio, and polypropylene fibers ratio) are plotted. The results of cracking loads, ultimate loads are presented through Figures 11-15, which represent the effect of different parameters and their effect on the slab behavior which are explained through the following sections:
5.4.1. Effect of Cross Section Shape of GFRP-Bars
The change of the cross sectional shape of bars from circular to square, resulted in an increase in the surface area of the reinforcement by 12.2%. Consequently, this improved the bond strength of the GFRP-bars with concrete, and did not result in any bond slippage. This change resulted in difference in the surface area of bars, which changed the cracking loads and the failure loads of the slabs reinforced by GFRP-bars. By looking into the test results, it was found that slab G-3S-25-1.5 reinforced with GFRP-square bars, fell at a much higher load than the slab reinforced with 16 mm diameter GFRP-bars (about 10% of the failure load). The cracking load changed
![]()
Figure 11. Effect of reinforcement type and bar cross section shape.
![]()
Figure 12. Difference in concrete cover and plane surface of square and circular bars.
![]()
Figure 13. Effect of concrete compressive strength.
![]()
Figure 15. Effect of polypropylene fiber ratio.
between slabs G-3S-25-1.5 and G-3C-25-1.5 by about 26.3%. The slab reinforced with steel bars S-3C-25-0, had higher failure and cracking load compared to the cracking and failure load for slabs reinforced with GFRP- bars with the same concrete characteristics strength of 25 MPa and the same reinforcement ratio. Figure 11 shows the effect of changing cross section of bar shape on the failure load.
Another factor affected by the change of the bar shape are the behavior controlled by splitting cracks. Splitting cracks occur unavoidably under increasing loads depending on a variety of physical and mechanical factors, such as confining pressure, concrete cover, transverse reinforcement and concrete toughness. The last being the basis of crack cohesion. Of course longitudinal splitting may be limited to the concrete closest to the bars (Partial splitting) if one or more of the above mentioned, depending on the interaction between bar and the concrete. Two types of interaction have been traditionally acknowledged. Pull out failure and splitting failure. In the former case bond failure is mainly due to the shearing of the concrete keys cast between each pair of lugs and this type of bond may not vary a lot between rectangular and circular bars. The type that is possibly affected which results from failure due to local mechanism (interface collapse) even if the whole bar is involved. The later case, bond failure is mostly due to longitudinal splitting of the concrete surrounding the bar. Bond capacity vanishes once the radial cracks get to the outer surface of the structural element. The failure is related to a sort of structural collapse since structural parameters other than those pertaining to bond enter the scene. The concrete cover thickness as well as the stress concentration on cover from the bar changes by the change of the shape of reinforcing bars. Therefore, the rectangular shape of the bar resuts in slightly lower bar hight when the bars are placed at the same level like circular bars slightly higher concrete cover thickness (see Figure 12). The slight difference in concrete cover thickness for rectangular bars causes an enhancement in the bond strength. Another point to be noted is that the plane surface of the square bar results in less stress concentration affecting the concrete cover unlike the circular bar section. Which is another factor causing enhancement of the behavious of slabs reinforced with square bars.
5.4.2. Effect of Concrete Compressive Strength
The cracking and failure loads were affected by changing the concret compressive strength of concrete mix. Where the slabs with higher concrete compressive strength had an improved material characteristics, the cracking and failure loads. The slab of 45 MPa concrete strength (G-3S-45-1.5) was higher than slabs of 35, and 25 MPa (G-3S-35-1.5 and G-3S-25-1.5) as shown in Figure 13. It can be seen that, increasing the concrete strength from 25 to 45 MPa, resulted in an increase of the ultimate and cracking loads by about 14% and 49% respectively.
5.4.3. Effect of Reinforcement Ratio
The slab reinforced with the lower reinforcement ratio G-3S-25-1.5 (ρf = 0.857%) showed a decrease in the cracking and failure load with respect to the slab reinforced with high reinforcement ratio G-5S-25-1.5 (ρf = 1.428%). However, increasing the reinforcement ratio from 0.857% to 1.428% for slabs reinforced with GFRP- square bars increased the failure and cracking load by about 28% and 72.7%, respectively as shown in Figure 14.
5.4.4. Effect of Adding Polypropylene Fibers to the Concrete Mix
Adding the polypropylene fibers to concrete mix, increased the cracking and failure loads of slabs reinforced with GFRP-square bars, because it improved the tensile characteristics of the concrete. While slab G-3S-25-0 reinforced with GFRP-square bars and without polypropylene fibers, showed lower cracking and failure loads compared to the slab G-3S-25-1.5 having polypropylene fibers by amount 14.7 N/m3. Also, the slab G-3S- 25-2.5 having polypropylene fibers by amount 24.5 N/m3, showed higher cracking and failure load than those slabs having amount 14.7 N/m3 as shown in Figure 15. It can be seen that, the polypropylene fibers by amount 14.7 N/m3, increased the cracking and failure load by 44% and 10% respectively compared to the slab without polyproylene. In addition, the slab with the polypropylene fibers by amount 24.5 N/m3, increased the cracking and failure load by 67.7% and 17% respectively.
5.5. Crack Pattern and Modes of Failure
Cracks in all of tested slabs were observed. Flexural cracks were initiated at the bottom surface of concrete slabs in the middle region between the two line loads, First crack appeared whenever the tensile stress exceeded the modulus of rupture of concrete. The crack appeared at middle of the slab and developed slowly across the width of the slab (i.e. parallel to the supports), and was accompanied by an increase in deflection due to stiffness reduction of the specimen. As the load increased, additional crack started to form along the length of the specimens between the two lines loads, and slowly propagated upward throughout the thickness of the slabs up to the failure. The crack distribution, width, and propagation were affected by the study parameters. The maximum crack width occurred in the specimen G-3C-25-1.5 and propagated fastest (reinforced with 3 circular GFRP-bars of 16 mm diameter) at the lowest level of loading. On other hand, the minimum crack width appeared and propagated at a slower rate in the specimen G-5S-25-1.5 (reinforced with 5 GFRP-square bars). For all slabs reinforced with GFRP bars the modes of failure started by crushing of concrete followed by the rupture of the GFRP reinforcements whereas the steel reinforced slab failed by yielding of the steel which was then followed by crushing of concrete. The propagation of crack pattern for all tested slabs is shown in Figure 16.
Figures 17-20 show typical load-strain relationships for reinforcement bars and concrete of RC slabs. The relationship consisted of a bilinear curve, low rate of strain increasing for a certain load increment up to the cracking load, and then higher rate of strain increasing for the same load increment when the concrete cracked but became also linear up to failure. In general, the strains of the slabs reinforced with GFRP-bars without enhancement were much higher than the steel sample due to the lower stiffness of the GFRP-bars. Enhancing parameters improved the strain values and became very close to the strain values of the steel sample.
![]()
Figure 17. Effect of reinforcement type and bar cross section shape on load-strain relationship.
![]()
Figure 18. Effect of concrete compressive strength on load-strain relationship.
![]()
Figure 19. Effect of reinforcement ratio on stress-strain relationship.
![]()
Figure 20. Effect of polypropylene fiber ratio on load-strain relationship.
6. Conclusions
This paper presented the fabrication and testing of new developed FRP bars. The physical and mechanical properties of a newly developed product of glass FRP-square and circular bars are presented. GFRP square bars were tested and compared with GFRP circular bars (16 mm diameter) and steel. The fabrication and testing of the bars and an experimental study of one-way concrete slabs reinforced with glass square and circular FRP bars and steel bars are presented. A total of 9 full-scale RC slabs were prepared to study the effect of five test parameters: type of reinforcement (steel versus GFRP), bar cross section shape, concrete compressive strength, reinforce- ment ration of longitudinal bars, and polypropylene fiber ratio. Based on the experimental test results presented in this paper, the following conclusions can be drawn:
1) The glass-fiber contents by weight of square-GFRP bars and circular-GFRP bars were 72.19% and 71.57%, respectively, which were made by 144 yarns. These results of fiber content are adopted with ACI 440.6M-08 and CSA S-807-10 (70% fiber content by weight or 55% as fiber content by volume).
2) The unit weight of square GFRP bars ranged between 15.69 to 25.6 KN/m3 according to the number of yarns which were used 80 - 144 yarns per bar.
3) The tensile strength, elastic tensile modulus, and ultimate strain of square-GFRP bars are 642 MPa, 47.5 GPa, and 1.36%, respectively. Moreover, the tensile strength, elastic tensile modulus, and ultimate strain of circular-GFRP bars (16 mm of diameter) are 630 MPa, 45.1 GPa, and 1.42%, respectively.
4) The behavior and ultimate flexural loads of concrete slabs reinforced with GFRP-square bars were improved compared with concrete slabs reinforced with GFRP-circular bars of 16 mm diameter.
5) Increasing the concrete compressive strength, resulted in improving the mechanical properties of the concrete mix for slab (G-3S-45-1.5) compared with slabs (G-3S-25-1.5, G-3S-35-1.5), consequently increasing the stiffness of slab and improved the behavior of concrete slabs with GFRP-square bars.
6) Slabs having the lowest reinforcement ratio gave the maximum deflections. This was very obvious, where in the slab having the minimum area of reinforcement of 3 bars (reinforcement ratio of 0.857%) had the maximum deflections. On the other hand, the slab having the maximum area of reinforcement of 5 bars (reinforcement ratio of 1.428%) had the minimum deflections.
7) The deflections of the slabs were inversely proportional to the amount of the polypropylene fibers added to the concrete mix. When the concrete mix had no polypropylene fibers, the deflections of the slabs were noticed. Adding the polypropylene fibers to the concrete mix decreased the deflections, and improved the behavior of concrete slabs reinforced with GFRP-square bars.
Acknowledgements
The authors would like to express their special thanks and gratitude to the technical staff of the structural lab of the Department of Civil Engineering, Faculty of Engineering at the Helwan University.
NOTES
*Corresponding author.