Discrete Inequalities on LCT

Guanlei Xu¹, Xiaotong Wang², Xiaogang Xu²

¹Ocean Department of Dalian Naval Academy, Dalian, China.
²Navgation Department of Dalian Naval Academy, Dalian, China.

DOI: 10.4236/jsip.2015.62014                

Abstract

Linear canonical transform (LCT) is widely used in physical optics, mathematics and information processing. This paper investigates the generalized uncertainty principles, which plays an important role in physics, of LCT for concentrated data in limited supports. The discrete generalized uncertainty relation, whose bounds are related to LCT parameters and data lengths, is derived in theory. The uncertainty principle discloses that the data in LCT domains may have much higher concentration than that in traditional domains.

Keywords

Linear Canonical Transform (LCT), Uncertainty Inequality

1. Introduction

In physics, the uncertainty principle plays an important role in elementary fields, and data concentration is often considered carefully via the uncertainty principle [1] - [8] . In continuous signals, the supports are assumed to be

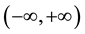, based on which various uncertainty relations [1] [2] [9] - [21] have been presented. However, in practice, both the supports of time and frequency are often limited. In such case, the support 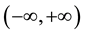fails to hold

true. In limited supports, some papers such as [22] - [25] have discussed the uncertainty principle in conventional time-frequency domains for continuous and discrete cases and some conclusions are achieved. However, none of them has covered the linear canonical transform (LCT) in terms of Heisenberg uncertainty principles that have been widely used in various fields [4] - [6] . Therefore, there has a great need to discuss the uncertainty relations in LCT domains. As the generalization of the traditional FT, FRFT [5] [6] [26] - [28] and so on, LCT has some special properties with more transform parameters (or freedoms) and sometimes yields the better result [29] . Readers can see more details on LCT in [6] and so on.

2. Preliminaries

2.1. Definition of LCT

Before discussing the uncertainty principle, we will introduce some relevant preliminaries. Here, we first briefly

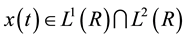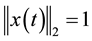review the definition of LCT. For given continuous signal and, its LCT [6] is defined as

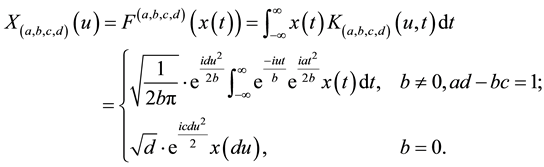(1)

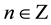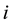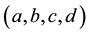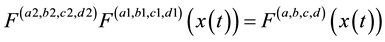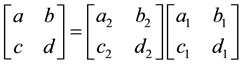where and is the complex unit, are the transform parameters defined as that in [6] . In addition, and. If 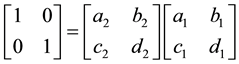, then 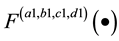and 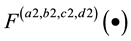are the LCT transform pairs, i.e., 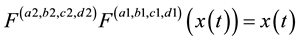. Also, if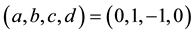, we have the following equations:

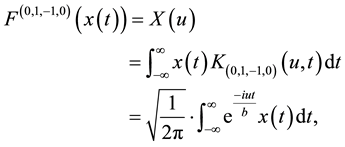and.

However, unlike the discrete FT, there are a few definitions for the DLCT (discrete LCT), but not only one. In this paper, we will employ the definition defined as follows [6] :

(2)

Clearly, if, (2) reduces to the traditional discrete FT [6] . Also, we can rewrite definition (2) as with and, where,.

For DLCT, we have the following property [5] [6] :

.

More details on DLCT can be found in [6] .

2.2. Frequency-Limiting Operators

Definition 1: Let be a complex-valued signal with and its LCT, if there is a function vanishing outside (is a measurable set) such that, then is -concentrated.

Specially, if, then definition 1 reduces to the case in time domain [22] [23] . If, then definition 1 reduces to the case in traditional frequency domain [22] [23] .

Definition 2: Generalized frequency-limiting operator is defined as

,.

If, then definition 2 is the time-limiting operator [22] [23] . If, then definition 2 is the traditional frequency-limiting operator [22] [23] . Definitions 1 and 2 disclose the relation between and. For the discrete case, we have the following definitions.

Definition 3: Let be a discrete sequence with and its DLCT, if there is a sequence satisfying such that, then is -concentrated. Here, is the 0-norm operator that counts the non-zero elements.

Definition 4: Generalized discrete frequency-limiting operator is defined as

with is the DLCT of and is the character function on.

Clearly, definitions 3 and 4 are the discrete extensions of definitions 1 and 2. They have the similar physical meaning. These definitions are introduced for the first time, the traditional cases [22] [23] are only their special cases. Definition 3 and 4 disclose the relation between and.

3. The Uncertainty Relations

3.1. The Uncertainty Principle

First let us introduce a lemma.

Lemma 3:

where is the Frobenius matrix norm.

Proof: From the definition of the operator in definition 4, we have

.

Exchange the locations of the sum operators, we obtain

Hence, according to the definition of the Frobenius matrix norm [1] and the definition of DLCT, we have

In the similar manner with the continuous case, we can obtain. Since, we have , thus, we get . Therefore, we can obtain the following theorem 2.

Theorem 2: Let be the DLCT of the time sequence for transform parameter, with -concentrated on index set . Let be the numbers of nonzero entries in (respectively). Then

.

3.2. Extensions

Set in theorem 2, we can obtain the following theorem 3 directly.

Theorem 3: Let be the DLCT of the time sequence with

length N. counts the numbers of nonzero entries in (respectively). Then

Clearly, theorem 3 is a special case of theorem 2. Also, this theorem can be derived via theorem 1 in [25] .

Differently, we obtain this result in a different way. Here we note that since, there is at least one non-zero element in every LCT domain for. Therefore, for.

Through setting special value for in theorem 3, we have

Corollary 1: with.

We can obtain the following more general uncertainty relation associated with DLCT.

Theorem 4: Let be the DLCT of the time sequence (and) with length and. counts the number of nonzero elements in. Then

with

Proof: From the assumption and the definition of DLCT [6] , we know

for.

where . Therefore, let, have [25]

where and with and with.

Hence, we obtain

Set, then

Using the triangle inequality, we have

hence

From and Parseval’s principle [6] , we obtain:

.

Hence

.

Therefore, we obtain

Adding all the above inequalities, we have with. Similarly, from and Parseval’s principle [6] , we obtain, hence

.

From the definition and property of DLCT [6] we have

with.

Hence, we finally obtain with. This theorem is the extension of theorem 3 and discloses the uncertainty relation between multiple signals.

4. Conclusion

In practice, for the discrete data, not only the supports are limited, but also they are sequences of data points whose number of non-zero elements is countable accurately. This paper discussed the generalized uncertainty relations on LCT in terms of data concentration. We show that the uncertainty bounds are related to the LCT parameters and the support lengths. These uncertainty relations will enrich the ensemble of uncertainty principles and yield the potential illumination for physics.

Acknowledgements

This work was fully supported by the NSFCs (61002052 and 61471412) and partly supported by the NSFC (61250006).

Supported

This work was fully supported by the NSFC (61002052) and partly supported by the NSFC (61250006 and 60975016).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Zhang, X.D. (2002) Modern Signal Processing. 2nd Edition, Tsinghua University Press, Beijing, 362.
[2]	Selig, K.K. (2002) Uncertainty Principles Revisited. Electronic Transactions on Numerical Analysis, 14, 165-177.
[3]	Dembo, A., Cover, T.M. and Thomas, J.A. (2001) Information Theoretic Inequalities. IEEE Transactions on Information Theory, 37, 1501-1508.
[4]	Loughlin, P.J. and Cohen, L. (2004) The Uncertainty Principle: Global, Local, or Both? IEEE Transac-tions on Signal Processing, 52, 1218-1227.
[5]	Folland, G.B. and Sitaram, A. (1997) The Uncertainty Principle: A Mathematical Survey. The Journal of Fourier Analysis and Applications, 3, 207-238. http://dx.doi.org/10.1007/BF02649110
[6]	Tao, R., Deng, B. and Wang, Y. (2009) Theory and Application of the Fractional Fourier Transform. Tsinghua University Press, Beijing.
[7]	Maassen, H. (1988) A Discrete Entropic Uncertainty Relation. Quantum Probability and Applications, Springer-Verlag, New York, 263-266.
[8]	Stern, A. (2007) Sampling of Compact Signals in Offset Linear Canonical Transform Domains. Signal, Image and Video Processing, 1, 359-367.
[9]	Shinde, S. and Vikram, M.G. (2001) An Uncertainty Principle for Real Signals in the Fractional Fourier Transform Domain. IEEE Transactions on Signal Processing, 49, 2545-2548.
[10]	Mustard, D. (1991) Uncertainty Principle Invariant under Fractional Fourier Transform. The Journal of the Australian Mathematical Society. Series B. Applied Mathematics, 33, 180-191. http://dx.doi.org/10.1017/S0334270000006986
[11]	Bialynicki-Birula, I. (1985) Entropic Uncertainty Relations in Quantum Mechanics. In: Accardi, L. and von Waldenfels, W., Eds., Quantum Probability and Applications II, Lecture Notes in Mathematics, Volume 1136, Springer, Berlin 90.
[12]	Aytür, O. and Ozaktas, H.M. (1995) Non-Orthogonal Domains in Phase Space of Quantum Optics and Their Relation to Fractional Fourier Transforms. Optics Communications, 120, 166-170. http://dx.doi.org/10.1016/0030-4018(95)00452-E
[13]	Stern, A. (2008) Uncertainty Principles in Linear Canonical Transform Domains and Some of Their Implications in Optics. Journal of the Optical Society of America A, 25, 647-652. http://dx.doi.org/10.1364/JOSAA.25.000647
[14]	Sharma, K.K. and Joshi, S.D. (2008) Uncertainty Principle for Real Signals in the Linear Canonical Transform Domains. IEEE Transactions on Signal Processing, 56, 2677-2683. http://dx.doi.org/10.1109/TSP.2008.917384
[15]	Zhao, J., Tao, R., Li, Y.L. and Wang, Y. (2009) Uncertainty Principles for Linear Canonical Transform. IEEE Transactions on Signal Processing, 57, 2856-2858. http://dx.doi.org/10.1109/TSP.2009.2020039
[16]	Xu, G.L., Wang, X.T. and Xu, X.G. (2009) Three Cases of Uncertainty Principle for Real Signals in Linear Canonical Transform Domain. IET Signal Processing, 3, 85-92. http://dx.doi.org/10.1049/iet-spr:20080019
[17]	Xu, G.L., Wang, X.T. and Xu, X.G. (2009) New Inequalities and Uncertainty Relations on Linear Canonical Transform Revisit. EURASIP Journal on Advances in Signal Processing, 2009, Article ID: 563265.http://dx.doi.org/10.1155/2009/563265
[18]	Xu, G.L., Wang, X.T. and Xu, X.G. (2009) Generalized Entropic Uncertainty Principle on Fractional Fourier Transform. Signal Processing, 89, 2692-2697. http://dx.doi.org/10.1016/j.sigpro.2009.05.014
[19]	Xu, G.L., Wang, X.T. and Xu, X.G. (2009) Uncertainty Inequalities for Linear Canonical Transform. IET Signal Processing, 3, 392-402. http://dx.doi.org/10.1049/iet-spr.2008.0102
[20]	Xu, G.L., Wang, X.T. and Xu, X.G. (2009) The Logarithmic, Heisenberg’s and Short-Time Uncertainty Principles Associated with Fractional Fourier Transform. Signal Processing, 89, 339-343. http://dx.doi.org/10.1016/j.sigpro.2008.09.002
[21]	Xu, G.L., Wang, X.T. and Xu, X.G. (2010) On Uncertainty Principle for the Linear Canonical Transform of Complex Signals. IEEE Transactions on Signal Processing, 58, 4916-4918. http://dx.doi.org/10.1109/TSP.2010.2050201
[22]	Somaraju, R. and Hanlen, L.W. (2006) Uncertainty Principles for Signal Concentrations. Proceedings of the 7th Australian Communications Theory Workshop, Perth, 1-3 February 2006, 38-42. http://dx.doi.org/10.1109/AUSCTW.2006.1625252
[23]	Donoho, D.L. and Huo, X. (2001) Uncertainty Principles and Ideal Atomic Decomposition. IEEE Transactions on Information Theory, 47, 2845-2862. http://dx.doi.org/10.1109/18.959265
[24]	Donoho, D.L. and Stark, P.B. (1989) Uncertainty Principles and Signal Recovery. SIAM Journal on Applied Mathematics, 49, 906-930. http://dx.doi.org/10.1137/0149053
[25]	Elad, M. and Bruckstein, A.M. (2002) A Generalized Uncertainty Principle and Sparse Representation in Pairs of Bases. IEEE Transactions on Information Theory, 48, 2558-2567. http://dx.doi.org/10.1109/TIT.2002.801410
[26]	Xu, G.L., Wang, X.T. and Xu, X.G. (2010) Novel Uncertainty Relations in Fractional Fourier Transform Domain for Real Signals. Chinese Physics B, 19, Article ID: 014203. http://dx.doi.org/10.1088/1674-1056/19/1/014203
[27]	Pei, S.C., Yeh, M.H. and Luo, T.L. (1999) Fractional Fourier Series Expansion for Finite Signals and Dual Extension to Discrete-Time Fractional Fourier Transform. IEEE Transactions on Circuits and System II: Analog and Digital Signal Processing, 47, 2883-2888.
[28]	Pei, S.C. and Ding, J.J. (2003) Eigenfunctions of the Offset Fourier, Fractional Fourier, and Linear Canonical Transforms. Journal of the Optical Society of America A, 20, 522-532. http://dx.doi.org/10.1364/JOSAA.20.000522
[29]	Qi, L., Tao, R., Zhou, S. and Wang, Y. (2004) Detection and Parameter Estimation of Multicomponent LFM Signal Based on the Fractional Fourier Transform. Science in China Series F, 47, 184-198. http://dx.doi.org/10.1360/02yf0456