On Historical Value at Risk under Distribution Uncertainty

Atsushi Iizuka¹, Yumiharu Nakano²

¹Informatix Inc., Kanagawa, Japan.
²Tokyo Institute of Technology, Tokyo, Japan.

DOI: 10.4236/jmf.2015.52010                

Abstract

We investigate the asymptotics of the historical value-at-risk under capacities defined by sublinear expectations. By generalizing Glivenko-Cantelli lemma, we show that the historical value-at-risk eventually lies between the upper and lower value-at-risks quasi surely.

Keywords

Value-at-Risk, Sublinear Expectation, Capacities, Glivenko-Cantelli Lemma

1. Introduction

In financial industry, the value-at-risk has been one of main tools for risk management (see, e.g., McNeil et al. [1] , and Föllmer and Schied [2] ). In this framework, the random variables for assets or asset returns are assumed to have distributions without uncertainty. In other words, it is implicitly assumed that there are true asset distributions and the estimation difficulty comes from our limited capability. However, it should be remarked that there is a possibility that the assets have the distribution uncertainty, i.e., the assets may have Knightian uncertainty (see Knight [3] ).

To capture the distribution uncertainty, the theory of sublinear expectation is introduced and developed (see Peng [4] [5] and the references therein). In this theory, the term probability is replaced by the ones of the upper and lower capacities induced by the upper and lower expectations, respectively, and the distribution uncertainty is described by the gap between the upper and lower expectations.

In this paper, we consider the value-at-risk type risk measure under the sublinear expectation, where the reference probability measure in the classical framework is replaced by the upper and lower capacities. We call these the upper and lower value-at-risk, respectively. Our aim is to study the asymptotic behavior of the historical value-at-risk under uncertainty. In doing so, we prove a generalization of Glivenko-Cantelli lemma under uncertainty, and then show that the historical value-at-risk eventually lies in between the upper and lower value- at-risks quasi surely.

This paper is organized as follows: In Section 2, we recall the theory of sublinear expectation. Section 3 is devoted to the statement of the main results and its proofs.

2. Sublinear Expectation and Capacities

In this section, we recall the basis of the sublinear expectation, introduced by Peng [4] . Let Ω be a given set and 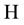a linear space of 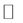-valued functions on Ω. We assume that whenever 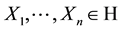and 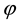is a bounded function on 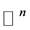or where denotes the linear space of functions on 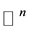satisfying

for some 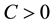and depending on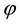. We call an element in 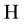a random variable.

We consider a sublinear expectation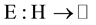, in the sense of [4] . Namely, E is assumed to be satisfy the following conditions: for any,

1) Monotonicity: if then.

2) Constant preserving: for.

3) Subadditivity:.

4) Positive homogeneity: for.

Moreover, we assume that for with for each. Then, by Theorem 2.1 and Remark 2.2 in [5] , there exists a set of probability measures on such that

where denotes the linear expectation with respect to. Then, the -valued set functions

define capacities, where 1_A denotes the indicator function of a set A. That is, each satisfies the following:

1),.

2) If satisfy then.

We refer to Denenberg [6] for the theory of capacities. Throughout this paper, we assume that each satisfies the following:

3) If satisfies, then.

4) If satisfies, then.

Let us recall several concepts in the sublinear expectation theory. The random variable is said to be independent of, where, , if

We say that and have the same distribution if

A sequence is called the one of independent, identically distributed random variables if and have the same distribution, and if is independent of for any. As in the linear case, we call a sequence of independent, identically distributed random variables an IID sequence. We say that the distribution of X has an uncertainty if is nonlinear in. In particular, set

Then if, then we say that X has the mean uncertainty. Similarly, X is said to have the volatility or variance uncertainty if.

3. Main Resutls

For any, we define the functions by

(1)

Proposition 3.1 Let and let and be as in (1). Then each satisfies the following:

1) for with.

2),.

3) for.

Proof. The assertion (1) follows from the monotonicity of and.

To prove (2), take and set. We will see for any sequence with. By setting we have and . It follows from the definition of the capacity that

Similarly, follows.

Finally, by an argument similar to the proof of (2) with, we can show for any sequence with, implying (3). □

The proposition above justifies the following definition:

Definition 3.2 For a random variable X, we call the function and as in (1) the upper and lower cumulative distribution functions of X, respectively.

For an IID sequence, the empirical distribution function of is defined by

If satisfies for some, then by Strong law of large number under sublinear expectation (see Theorem 1 in Chen [7] ),

(2)

Indeed,

We show a stronger result, which is a generalization of Glivenko-Cantelli lemma.

Theorem 3.3 Let be an IID sequence with for some. Denote by and

the upper and lower cumulative distribution functions of X respectively, and denote by the empirical disribution function of. Then,

We need the following lemma for the proof of the theorem.

Lemma 3.4 Under the assumtions imposed in Theorem 3.3, for, there exist and

such that and

where, , for each.

Proof. Let. Then there exists such that. Starting with, we recursively define by

By this recursion, we can find such that or hold, and set. With this sequence, the lemma follows. □

With the help of Lemma 3.4, we can show Theorem 3.3.

Proof of Theorem 3.3. Let be fixed. By Lemma 3.4, there exists a partion of such that and

(3)

By (2), we have, for any, where

Thus, for any and so for any. Hence

,

where for

So we have

Now, for any there exists j such that. Thus, by (3),

so

Therefore, on, letting we get and for all. Thus

If we write for the event inside the brace above and denote, then by the continuity of the capacity

meaning the assertion of the theorem. □

Recall that for a function satisfying (1)-(3) in Proposition 3.1 and for, the - quantile of F is defined by

Then we have the following:

Theorem 3.5 Let be an IID sequence with for some. Denote by and the upper and lower cumulative distribution functions of X respectively, and denote by the empirical disribution function of. Consider the upper, lower, and historical value-at-risk defined respectively by

Suppose that for

(4)

Then, the historical value-at-risk eventually lies in between the upper and lower value-at-risk, i.e.,

Proof. Consider the event A defined by

In view of Theorem 3.3, it suffices to show that for a given and there exists such that

(5)

To this end, fix and set,. By the definition of the infimum and the condition (4),

Thus we can take such that

Next, take such that

and set. Then,

So we have. Similarly, we see

leading to. Thus (5) follows. □

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	McNeil, A. J., Frey, R. and Embrechts, P. (2005) Quantitative Risk Management: Concepts, Techniques and Tools. Princeton University Press, Princeton.
[2]	Föllmer, H. and Schied, A. (2004) Stochastic Finance: An Introduction in Discrete Time. 2nd Edition, Walter de Gruyter, Berlin. http://dx.doi.org/10.1515/9783110212075
[3]	Knight, F.H. (1921) Risk, Uncertainty, and Profit. Houghton Mifflin, Boston.
[4]	Peng, S. (2006) G-Expectation, G-Brownian Motion and Related Stochastic Calculus of Itô’s type, In: Benth, F.E., et al., Eds., Stochastic Analysis and Applications: The Abel Symposium 2005, Springer-Verlag, Berlin, 541-567.
[5]	Peng, S. (2010) Nonlinear Expectations and Stochastic Calculus under Uncertainty. arXiv:1002.4546[math.PR]
[6]	Denneberg, D. (1994) Non-Additive Measure and Integral. Kluwer Academic Publishers, Dordrecht. http://dx.doi.org/10.1007/978-94-017-2434-0
[7]	Chen, Z. (2010) Strong Laws of Large Numbers for Capacities. arXiv:1006.0749[math.PR]