1. Introduction
The glucose fuel cells use glucose as a fuel to produce electrical energy [1] -[5] , and they use enzymes as biocatalyst to convert directly chemical or biochemical energy into electrical energy [6] -[9] . Enzymatic catalysts for glucose fuel cells have excellent selectivity and can generate power densities of the order of several mW・cm−2 [10] [11] . Finally, in glucose enzymatic fuel cells enzymes convert the glucose into water and carbon dioxide. Modelling biofuel cells play important role in understanding and developing new devices. The enzymatic fuel cells mathematical models are based on a system of non-linear equations, including reaction kinetics, transport phenomena [12] [13] , statistical analysis [14] , metabolic analysis [15] . There is a single channel [12] for flow of each anolyte and catholyte streams. An exponential decay in the availability of oxygen from the cathode side was observed [16] [17] . Various authors have used theoretical numerical and experimental methods for estimating the fuel cell performance [18] -[21] . Majority of modelling are numerical and based on mediator electron transfer mechanism and membrane used fuel cells [7] [21] [22] . The focus of this paper is to develop a theoretical analytical model for enzymatic membraneless glucose fuelled fuel cell, with direct electron transfer and enzymes are immobilized on an electrode surface. The present study aimed to predict a hydrogen ions current, an electrical voltage and an electrical power in enzymatic fuel cells, based on basic chemical and electro physical principles.
2. Theory
In general, biofuel cells transfer electrons to an electrode either directly (direct electron transfer) or through mediator molecules (mediated electron transfer) [23] . The model presented here bases on experimental results with direct electron transfer fuel cell that were reported at [8] . The model includes two parallels plane each other electrodes. Electrodes are separated by a membraneless reservoir, between electrodes, containing an electrolyte (phosphate buffer) solution, enables ions movement between the electrodes. The fuel reservoir with a glucose solution is positioned left to the anode.The electrodes consisted of carbon cloth with gold or silver. The enzymes (glucose oxidase) are immobilized to an anode. The electrochemical reaction is the oxidation of glucose to gluconic acid gives two electrons and two protons [24] . Hydrogen ions generated on the anode and move from the anode to the cathode through the liquid bulk. The cathode is exposed to air and the porous cathode allows oxygen to pass. On the cathode, oxygen reacts chemically with the electrons from the external circuit and with the hydrogen ions from the electrolyte to yield water [8] . Michaelis-Menten equation [25] for rate of a volume hydrogen ions generationg01 was adapted [8] to surface g1S (Equation (1)) hydrogen ions generation
 (1)
(1)
It gives the surface reaction rate g1S as a function of glucose concentration [G] and a surface enzyme concentration [ES]. Here the kinetic enzyme reaction rates are kcat and KM. Note, that a connection between [ES] and volume enzyme concentration [ET] can be taken as [ES] = L[ET], where L is a thickness of an enzyme layer.
2.1. Mathematical Model
Enzymatic anode. The model is assumed to be in steady state in regards to proton production and consumption. Enzymes are immobilized homogeneously and can be directly oxidized on the electrode surface. An enzyme layer has a uniform thickness. A buffer solution is assumed to be electrically neutral. Hydrogen ions, generated on an anode, are moving towards a cathode, were they are consumed. A current density is assumed here to be one dimensional along the x-axis. The axis x is normal to both of electrodes. The point x = 0 on an axis x represents the surface between the enzymatic anode and a glucose reservoir, x = L is the boundary between the enzymatic anode and the buffer solution, x = d is the boundary between the buffer solution and the cathode. The thickness of the cathode doesn’t take into consideration in this paper. The kinetics and mass transport in the enzyme layer (0 < x < L) can be represented as follow differential equations for hydrogen ions (Equation (2)), that describes concentration changes as a function of the distance:
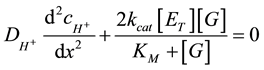 (2)
(2)
and for glucose
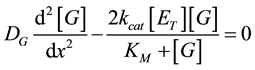 (3)
(3)
where DG, 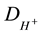 are diffusion coefficients of glucose and hydrogen ions respectively,
are diffusion coefficients of glucose and hydrogen ions respectively, 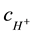 is hydrogen ions concentration
is hydrogen ions concentration
2.2. Bulk Solution
In the bulk (L < x < d) the mass conservation equation of solute species in a steady state conditions for the current density of hydrogen ions 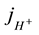 converts to form (4):
converts to form (4):
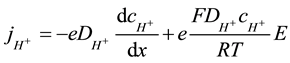 (4)
(4)
Here e signed electron ionic charge, E is an electrical field, F―Faraday constant, R―universal gas constant, T―temperature.
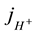 is a current density of ions present in the solution during the fuel cell operations. The total current density j is made up of contribution from all species.
is a current density of ions present in the solution during the fuel cell operations. The total current density j is made up of contribution from all species.
Outside the enzyme layer in the bulk (L < x < d) the hydrogen ions behaviour if the only diffusion takes place can be expressed by the Equation (5).
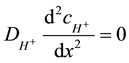 (5)
(5)
The solution these Equations (2) (3) (5) gives hydrogen concentration along axis x which finally uses to calculate a voltage and a power of a fuel cell.
2.3. Boundary Conditions
The boundary conditions between two regions mean the equal species fluxes through the same surface and conditions of a continuity for concentrations. The diffusion coefficients of hydrogen ions are different in these two regions. Equations (6) (7) describe the following boundary conditions between the anode and the bulk where x = L for hydrogen ions:
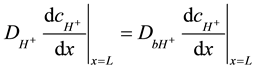 (6)
(6)
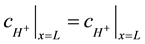 (7)
(7)
where 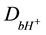 are diffusion coefficients of hydrogen ions in the bulk solution.
are diffusion coefficients of hydrogen ions in the bulk solution.
The concentration of the hydrogen ions at the anode surface where x = 0 was taken
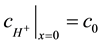 (8)
(8)
where c0 is the hydrogen ions concentration between the glucose reservoir and an anode. The concentration of glucose at an anode surface (x = 0) was taken as:
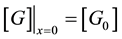 (9)
(9)
where  is the glucose concentration in the glucose reservoir. The current density is proportional to rate of an electrochemical reaction of a unit surface electrode. An amount of charge is proportional to the amount of material passed through the interface. This yields for another boundary condition
is the glucose concentration in the glucose reservoir. The current density is proportional to rate of an electrochemical reaction of a unit surface electrode. An amount of charge is proportional to the amount of material passed through the interface. This yields for another boundary condition
 (10)
(10)
Here z expressed the number of elementary ionic charges. Boundary conditions for cathode at a point x = d defined as:
![]() (11)
(11)
or
![]() (12)
(12)
where cd is the hydrogen ions concentration between the electrolyte reservoir and cathode, g2S is a rate of surface hydrogen ions consumption on a cathode surface.
2.4. Hydrogen Ions Concentration
The solution Equation (3) when ![]() with boundary conditions (9, 10) gives glucose concentration along axis x in a region 0 < x < L. (Note, than kM = 0.019 M, [G] = 1 M [8] ) Substituting this solution into the differential Equation (2) for hydrogen ions in a region (0 < x < L) yields follow Equation (13)
with boundary conditions (9, 10) gives glucose concentration along axis x in a region 0 < x < L. (Note, than kM = 0.019 M, [G] = 1 M [8] ) Substituting this solution into the differential Equation (2) for hydrogen ions in a region (0 < x < L) yields follow Equation (13)
![]() (13)
(13)
From Equations (5) (13) with boundary conditions (6, 7, 8, 11) the hydrogen ions concentration in region (0 < x < L) can be obtain as:
![]() (14)
(14)
And hydrogen ions concentration in a bulk (L < x < d) yields (Equation (15)):
![]() (15)
(15)
2.5. Current
The current is the flux at the electrode surface, that is a current density of a fuel cell yields
![]() (16)
(16)
Since a flux at the electrode surface where x = 0 caused by the rate g1S of hydrogen ions generation from an anode surface per unit of time the appropriate equation for gradient can be written as:
![]() (17)
(17)
Substituting Equations (1) (17) into Equation (16) yields
![]() (18)
(18)
The Equation (18) reveals that a current density is proportional to a rate of electrochemical reactions kcat in a fuel cell, enzyme concentrations and a thickness of enzyme layer. In case of direct electron transfer increases number of electrons involved in reactions linearly increases a current density. It means that electrical characteristics of fuel cells can be significantly improved by using some types of enzyme catalyst that diverted more than two electrons to the electrode.
Actually, the current can be computed as well from the hydrogen ions concentration (Equation (14)):
![]() (19)
(19)
When a value of glucose concentration [G] is much greater than kM both Equations (18) (19) reduce (with
![]() ) to the simple form
) to the simple form
![]() (20)
(20)
This yields the same value of a calculated current in both cases. These equations suggest clear ways to achieve increasing a current density and as a consequence an electrical power density: increase kcat, thickness of an enzymatic layer L and a total enzyme concentration [ET].
2.6. Electrical Power
In general a power P, for an electrical circuit with an external load resistance RL and with electrical source![]() , which has an internal electrolyte resistance rO resistance between electrodes, can be expressed as
, which has an internal electrolyte resistance rO resistance between electrodes, can be expressed as
![]() (21)
(21)
where I is the current that equals to
![]() (22)
(22)
Difference potentials of electrical source ![]() for high hydrogen ions concentration estimated by Equations (4) (15) lead to
for high hydrogen ions concentration estimated by Equations (4) (15) lead to
![]() (23)
(23)
The result is similar to [8] . Here cL is the hydrogen ions concentration at the point x = L between the anode and electrolyte reservoir. Many factors are affecting losses in a fuel cell: mass transfer, electron transfer, chemical reactions, surface reactions etc. [26] . If take into consideration these factors and Equations (21)-(23) an power density ![]() of a fuel cell can be expressed in a follow form:
of a fuel cell can be expressed in a follow form:
![]() (24)
(24)
where A is an anode area, ri [Ohm] represents resistances of losses in a fuel cell like electrode reaction resistances, mass transfer, charge transfer etc. This expression shows, as expected, that minimizing the electrolyte resistance and the others resistance of losses in a fuel cell is essential way to increase a power. The maximal power density ![]() can be estimated by using Equations (19) and (23), that is:
can be estimated by using Equations (19) and (23), that is:
![]() (25)
(25)
3. Results and Discussion
3.1. Model Parameters
The system of equations that described above was solved using the program Mathematica 8. The parameters are using to validate this model (except the Section 3.3) were measured by [8] : the temperature 23˚C, the distance between electrodes d was 0.003 - 0.004 m. The thickness of an enzyme layer L was estimated 0.001 - 0.0005 m, the glucose concentration [G] = 1 M, [ET] = 10−6 - 10−5 M, kM = 0.019 M, kcat = 103 sec−1, the hydrogen ion diffusion coefficient in water was taken as ![]() [20] . The ratio
[20] . The ratio ![]() between diffusion coefficients
between diffusion coefficients ![]() in an area 0 < x < L and
in an area 0 < x < L and ![]() in a bulk L < x < d varies. There is
in a bulk L < x < d varies. There is ![]() for different calculations.
for different calculations.
3.2. Hydrogen Ions Concentration
Generated hydrogen ions are moving towards cathode and consuming there. During this process a gradient of hydrogen ions exists between the electrodes in a region L < x < d. A voltage, a current density and an electrical power of fuel cells depend on concentrations and a gradient of hydrogen ions. Therefore it is important to evaluate concentrations and a gradient of hydrogen ions in a fuel cell. The hydrogen ions concentration in the region 0 < x < L was calculated by Equation (14). The concentrations as a function of the distance x, when 0 < x < L (Figure 1) are plotted for different diffusion coefficients of hydrogen ions and different values of total enzyme concentrations.
Figure 1: The concentration of hydrogen ions (M) in a region (0 < x < L) (Equation (14)) is plotted against x for different total enzyme concentrations [ET].![]() ,
,![]() . Lines from top to the bottom
. Lines from top to the bottom ![]() respectively.
respectively.
Figure 1 demonstrates that the hydrogen ions concentration depends of a ratio ![]() hydrogen ions diffusion coefficients. The hydrogen ions concentration increases with this ratio and a total enzyme concentration. A thickness of enzyme layer and an enzyme concentration influences on the boundary concentration cL and as a consequences on a voltage and a power.The hydrogen ions concentration in a bulk L < x < d was calculated by Equation (15). The hydrogen ions concentrations in a bulk as a function of the distance x, when L < x < d (Figure 2), are plotted for different ratio of diffusion coefficients and different values of a total enzyme concentration.
hydrogen ions diffusion coefficients. The hydrogen ions concentration increases with this ratio and a total enzyme concentration. A thickness of enzyme layer and an enzyme concentration influences on the boundary concentration cL and as a consequences on a voltage and a power.The hydrogen ions concentration in a bulk L < x < d was calculated by Equation (15). The hydrogen ions concentrations in a bulk as a function of the distance x, when L < x < d (Figure 2), are plotted for different ratio of diffusion coefficients and different values of a total enzyme concentration.
Figure 2: The concentration of hydrogen ions (M) in a bulk (region L < x < d) (Equation (15)) is plotted against x for different total enzyme concentrations [ET].![]() ,
,![]() . Lines from top to the bottom
. Lines from top to the bottom ![]() respectively,
respectively,![]() .
.
Figure 2 demonstrates that the hydrogen ions concentrations in the bulk also depend of a ratio hydrogen ions diffusion coefficients ![]() and growing with it. The hydrogen ions concentration in the bulk increases with a total enzyme concentration. The gradient of hydrogen ions changes with a boundary concentration cd. Actually, the main factors that determine a hydrogen ions gradient in fuel cells are type electrodes in used, the
and growing with it. The hydrogen ions concentration in the bulk increases with a total enzyme concentration. The gradient of hydrogen ions changes with a boundary concentration cd. Actually, the main factors that determine a hydrogen ions gradient in fuel cells are type electrodes in used, the
![]()
Figure 1. The concentration of hydrogen ions (M) in a region (0 < x < L) (Equation (14)) is plotted against x for different total enzyme concentrations [ET].![]() ,
, ![]() = 0.8. Lines from top to the bottom [ET] = 0.7 × 10−5 M, 0.5 × 10−5 M 0.3 × 10−5 M 0.1 × 10−5 M respectively.
= 0.8. Lines from top to the bottom [ET] = 0.7 × 10−5 M, 0.5 × 10−5 M 0.3 × 10−5 M 0.1 × 10−5 M respectively.
![]()
Figure 2. The concentration of hydrogen ions (M) in a bulk (region L < x < d) (Equation (15)) is plotted against x for different total enzyme concentrations [ET].![]() , d = 4 × 10−3 m,
, d = 4 × 10−3 m, ![]() = 0.8. Lines from top to the bottom [ET] = 0.7 × 10−5 M, 0.5 × 10−5 M, 0.3 × 10−5 M, 0.1 × 10−5 M respectively.
= 0.8. Lines from top to the bottom [ET] = 0.7 × 10−5 M, 0.5 × 10−5 M, 0.3 × 10−5 M, 0.1 × 10−5 M respectively.
total enzyme concentration, a thickness of enzyme layer and basic kinetic parameters. As a result, they determine an electrical power of a fuel cell.
3.3. Current Density and Electrical Power
Glucose fuel cell with glucose oxidase enzymatic filter paper was described in [6] ([G] = 10 mM, buffer phosphate, obtained typical current density range (5 - 20) mA/cm2 and open circuit voltage around 0.18 V). Carbon nanotubes serve to promote conduction and help immobilize the enzymes. Design was simplified by removing membrane. We think the represented here model can explain these experimental results. The dependence current density on enzyme concentration and an enzyme layer thickness was obtained from expression (19) (Figure 3). The effect of enzyme concentration and an enzyme layer thickness is linear with a current density, hence increasing either enzyme concentration and enzyme layer thickness has an important effect on the fuel cell.
Lines from top to the bottom glucose concentration [G] = 0.1 M, 0.01 M, 0.001 M respectively, total enzyme concentration ET = 10−5 M, 0.5 ´ 10−5 M, 10−6 M respectively.Calculations reveal that current density increases with a glucose concentration. For very low glucose concentration below 0.01M changing of a current density is almost linear with glucose concentration.
Eventually, according to Equation (19), a saturated value of a current density is independent of further increasing in glucose concentration. The maximal power density ![]() was calculated by Equation (25) when j = (5 - 20) mA/cm2 and voltage around 0.18 V. This gives range about 0.9 - 4 mW/cm2. Calculated values of a current density and a power density have a good agreement with measurements [6] . Power density
was calculated by Equation (25) when j = (5 - 20) mA/cm2 and voltage around 0.18 V. This gives range about 0.9 - 4 mW/cm2. Calculated values of a current density and a power density have a good agreement with measurements [6] . Power density ![]() decreases, after achieved a max value, with rising an external resistance and as consequence of a current reduction (Figure 4).
decreases, after achieved a max value, with rising an external resistance and as consequence of a current reduction (Figure 4).
Lines from top to the bottom a relation is![]() , 50 respectively.Because a fuel cell [6] has a very small current,
, 50 respectively.Because a fuel cell [6] has a very small current, ![]() is orders of magnitude higher than the most of the other losses.If an external resistance increases hence a current declines, current is reciprocal to resistance. Figure 4 demonstrates the plots corresponding to the examined power density.
is orders of magnitude higher than the most of the other losses.If an external resistance increases hence a current declines, current is reciprocal to resistance. Figure 4 demonstrates the plots corresponding to the examined power density.
4. Conclusion
In this paper an analytical model for enzymatic membraneless fuel cell with direct electron transfer was devel- oped. The adequacy of the model was estimated by comparison with fuel cells parameters. The calculated voltage, current and power density of this model were compared with the experimental parameters. The results reveal the dependence electrical power on hydrogen ions boundary concentrations and as consequences on the rate of hydrogens ions generation and consumption, thickness of enzyme layer, enzyme concentrations, and kinetics
![]()
Figure 3. Hydrogen’s ions current density (axis y) (Equation (19)) is plotted against total enzyme concentration (axis x). L = 5 × 10−4 m. Lines from top to the bottom glucose concentration [G] = 0.1 M, 0.01 M, 0.001 M respectively. Lines from top to the bottom total enzyme concentration ET = 10−5 M, 0.5 × 10−5 M, 10−6 M respectively.
![]()
Figure 4. Power density (axis y) (Equation (24)) is plotted against external resistance RL (axis x) when 0.01 Ohm < RL. < 1 Ohm, r0 = 0.16 Ohm, anode area A = 4 cm2. Lines from top to the bottom relation is cL/cd = 5 × 103, 50 respectively.
reaction rate coefficients. Hence, power can be increased with rising electrode surface. It can be achieved by increasing a porosity of electrode. Utilizing carbon nanotubes, metallic nanoparticles electrodes can significantly improve porosity. Efficient electrical communication by increasing the catalytic power of enzyme increases the rate of hydrogen ions generation and consumption, and leads to higher values of electrical parameters of fuel cell. The developed model can be used as framework for an analytic examination and an investigation of the effects of various parameters of the fuel cell to optimize a membraneless fuel cell with direct electron transfer.