Conservation of Forestry Biomass with the Use of Alternative Resource ()
1. Introduction
Forest is an integral part of our biosphere. It used for fuel, furniture etc. and thus provides strong foundation for the development of any country. Forest assists in the global cycling of water, oxygen, carbon and nitrogen. In many developing countries, people burn wood to get energy for heating and cooking. Forest also provides food and shelter to many wild life species. Due to overpopulation, industrialization and associated pollution forests are depleted alarmingly. A typical example is the Doon Valley in the northern part of India where the forestry resources are being depleted by limestone quarries, wood and paper based industries, growth of human and livestock populations, expansion of forest land for agriculture and settlement etc., threatening the ecological stability of the entire region [1] . It is therefore required a suitable harvesting plan to keep ecological balance. For controlling depletion of forestry biomass, alternative resources like synthetic, liquid wood, plastic, wood composite lumber etc. can play an important part. The following examples also motivate us to consider biomass- industry system with alternative resource.
1) To overcome the worldwide problem of conservation of forestry resources, synthetic is a good alternative of wood based product as it is cheap, and needs not much maintenance, and the one most important thing is that it looks fresher than wood based products.
2) Plastic and wood composite lumber are quickly becoming a common replacement for redwood, cedar, and treated lumber in such applications as decking, door and window frames, and exterior moldings. Redwood and cedar decking use virgin trees, maintaining our dependence on scarce wood resources. Plastic and wood composite lumber are worked similarly to real wood and do not require treatment, yet they hold up well to water, sun, insects, and salt air, typical enemies of wood [2] .
[3] proposed and analyzed a mathematical model for the survival of a resource-dependent biological population (such as human beings) where both the population and its resource were affected by a toxicant emitted into the environment from external sources as well as formed by its precursors. [4] investigated a nonlinear mathematical model to study the depletion of forestry resources caused by population and population pressure augmented industrialization. It is shown that the equilibrium density of resource biomass decreases as the equilibrium densities of population and industrialization increase. It is found that even if the growth of population (whether intrinsic or by migration) is only partially dependent on resource, still the resource biomass is doomed to extinction due to large population pressure augmented industrialization. It is noted that for sustained industrialization, control measures on its growth are required to maintain the ecological stability. In [5] , they proposed a nonlinear mathematical model and analyzed to study the survival of resource-dependent competing species. It is assumed that competing species and its resource are affected simultaneously by a toxicant emitted into the environment from external sources as well as formed by precursors of competing species. It is concluded from the analysis that as the cumulative rates of emission and formation of toxicants into the environment increase, the densities of both competing species and its resource decrease. [6] studied the effect of alternative resource (synthetic) on the conservation of forestry biomass which grew logistically decays due to presence of wood based industries.
In same year, [7] studied the effect of time delay on conservation of forestry biomass by proposing a non- linear mathematical model. They assumed that the density of forestry biomass depleted due to the presence of human population and it was being conserved by applying some technological efforts. Further, [8] and [9] investigated and concluded a nonlinear mathematical model to study the depletion of forest resources caused by population and the corresponding population pressure.
As a consequence, we propose a model for the interaction of forestry biomass with industrialization pressure, toxicant pressure and applied technological effort. Further, the effect of alternative resource on the growth of forestry biomass is seen. The time delay is the inherent property of the dynamical systems and plays an important role in almost all branches of science and particularly in the biological sciences. In the further study of the model, we see the effect of time delay on the growth rate of forestry biomass. The rest of this paper is organized as follows: In Section 2, we analyze our model with regard to equilibria and their positive conditions. In Section 3, we investigate the stability of positive equilibrium and stability and direction of Hopf bifurcation. In Section 4, some numerical supports are carried out to justify the analytic results obtained in the manuscript. Section 5 deals with the conclusions of the paper.
2. Mathematical Model
We consider the following system of differential equations:
 (1)
(1)
where ,
, .
.
In model system (1),  and
and 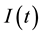 are the concentration of forestry biomass and industries, respectively.
are the concentration of forestry biomass and industries, respectively.  and
and 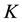 are intrinsic growth rate and carrying capacity of biomass and
are intrinsic growth rate and carrying capacity of biomass and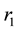 ,
,  are intrinsic growth and carrying capacity of industries, respectively.
are intrinsic growth and carrying capacity of industries, respectively.  and
and  represents the depletion rate of forest biomass and growth rate of industries in presence of forestry biomass. In the above system (1), growths of industries are based on forestry biomass. For controlling depletion of forestry biomass, alternative resources can play an important role. Using alternative resource
represents the depletion rate of forest biomass and growth rate of industries in presence of forestry biomass. In the above system (1), growths of industries are based on forestry biomass. For controlling depletion of forestry biomass, alternative resources can play an important role. Using alternative resource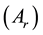 , the model (1) can be formulated as
, the model (1) can be formulated as
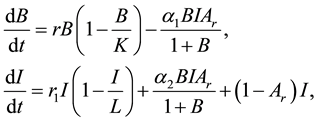 (2)
(2)
where ,
, .
.
Here  is a time independent constant and its origin is the alternative resource. If
is a time independent constant and its origin is the alternative resource. If![]() , the industries depend only on the forestry biomass and thus it is clear that the system (1) is special case of system (2). If
, the industries depend only on the forestry biomass and thus it is clear that the system (1) is special case of system (2). If ![]() then both the forestry biomass and industries grow without any interaction. In such case, the industries pressure on forestry biomass is completely removed and industries evolve in presence of alternative food only. But such decoupled system is out of our interest. For neglecting above both cases,
then both the forestry biomass and industries grow without any interaction. In such case, the industries pressure on forestry biomass is completely removed and industries evolve in presence of alternative food only. But such decoupled system is out of our interest. For neglecting above both cases, ![]() always lies between 0 and 1 in our system. Due to advancement in technology and industrialization at rapid pace, large amount of toxicants enter into both aquatic ant terrestrial environment and affect biomass. Let us assume that
always lies between 0 and 1 in our system. Due to advancement in technology and industrialization at rapid pace, large amount of toxicants enter into both aquatic ant terrestrial environment and affect biomass. Let us assume that ![]() is the concentration of toxicant in the environment at time
is the concentration of toxicant in the environment at time![]() . Emission of toxicant into the environment from various external sources and industries is
. Emission of toxicant into the environment from various external sources and industries is ![]() and
and![]() . The constant
. The constant ![]() is the natural washout rate coefficient of toxicant present in the environment,
is the natural washout rate coefficient of toxicant present in the environment, ![]() and
and ![]() are the depletion rate coefficients of toxicant concentration in the environment due to its uptake by the forestry biomass. After adding this in system (2), our extend model is as follows:
are the depletion rate coefficients of toxicant concentration in the environment due to its uptake by the forestry biomass. After adding this in system (2), our extend model is as follows:
![]() (3)
(3)
Here![]() .
.
Where![]() ,
, ![]() ,
,![]() .
.
The system (3) is further modified when the technological effort ![]() is applied to conserve the biomass. Thus system (3) become as:
is applied to conserve the biomass. Thus system (3) become as:
![]() (4)
(4)
where ![]() for
for![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Here ![]() is the measure of effort due to technology applied for conservation of forestry and
is the measure of effort due to technology applied for conservation of forestry and ![]() is the growth rate coefficient of forestry biomass due to technological effort. The constant
is the growth rate coefficient of forestry biomass due to technological effort. The constant ![]() is the growth-rate coefficient of technological efforts and
is the growth-rate coefficient of technological efforts and ![]() is the natural depletion-rate coefficient of technological effort.
is the natural depletion-rate coefficient of technological effort.
Lemma: The region of attraction for the model system (4) is given by the set:
![]()
where![]() ,
, ![]() ,
, ![]() and
and ![]() and it attracts all solutions initiating in the interior of the positive octant.
and it attracts all solutions initiating in the interior of the positive octant.
Equilibrium analysis: It can be checked that system (4) has four nonnegative equilibria namely,
![]() ,
, ![]() ,
, ![]() and
and![]() . The existence of the equilibrium point
. The existence of the equilibrium point ![]() is obvious hence omitted. We show the existence of the other equilibria as follows:
is obvious hence omitted. We show the existence of the other equilibria as follows:
Existence of ![]()
Here ![]() and
and ![]() are the positive solutions of the following algebraic equations:
are the positive solutions of the following algebraic equations:
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() . (7)
. (7)
From Equation (7), we get
![]() .
.
Thus, ![]() exists if:
exists if: ![]() which is obvious.
which is obvious.
From Equation (6), we get
![]() .
.
Putting the value of ![]() and
and ![]() in Equation (5), we get
in Equation (5), we get
![]()
Thus, ![]() exists if condition
exists if condition ![]() holds.
holds.
Existence of ![]()
Here ![]() and
and ![]() are the positive solutions of the following algebraic equations:
are the positive solutions of the following algebraic equations:
![]() , (8)
, (8)
![]() , (9)
, (9)
![]() . (10)
. (10)
From Equation (10), we get
![]()
From Equation (8), we get
![]() .
.
Putting the value of ![]() in Equation (9), we get
in Equation (9), we get
![]()
Existence of ![]()
Here ![]() and
and ![]() are the positive solutions of the following algebraic equations:
are the positive solutions of the following algebraic equations:
![]() , (11)
, (11)
![]() , (12)
, (12)
![]() , (13)
, (13)
![]() (14)
(14)
From Equation (14), we get
![]()
After simple manipulation, we get from Equation (12) is
![]()
Putting the value of ![]() in Equation (13), we get
in Equation (13), we get
![]()
Putting the value of![]() ,
, ![]() and
and ![]() in Equation (11), we get
in Equation (11), we get
![]() (15)
(15)
where
![]() (16)
(16)
We note that ![]() and
and![]() , showing the existence of
, showing the existence of ![]() in the interval
in the interval![]() . Now, the sufficient condition for
. Now, the sufficient condition for ![]() to be unique positive real is
to be unique positive real is ![]() at
at![]() , where
, where
![]() .
.
Remark 1. From Equation (15), it is easy to note that ![]() and
and![]() , which implies that the equili-
, which implies that the equili-
brium density of forestry biomass increases as the growth rate coefficient of technological efforts and value of alternative resources increases.
2.1. Local Stability Analysis without Delay, (i.e.![]() )
)
To discuss the local stability of system (4), we compute the variational matrix of system (4). The entries of general variational matrix are given by differentiating the right side of system (4) with respect to![]() and
and ![]() i.e.
i.e.
![]()
where
![]()
The variational matrix ![]() at equilibrium point
at equilibrium point ![]() is given by
is given by
![]()
The eigenvalues of matrix ![]() in the direction of
in the direction of ![]() and
and ![]() are negative. So
are negative. So ![]() has stable manifold in
has stable manifold in ![]() plane and unstable manifold in
plane and unstable manifold in ![]() -direction. The equilibrium point
-direction. The equilibrium point ![]() is stable manifold in
is stable manifold in ![]() plane if
plane if ![]() otherwise it becomes unstable in
otherwise it becomes unstable in ![]() plane.
plane.
The variational matrix ![]() at equilibrium point
at equilibrium point ![]() is given by
is given by
![]()
where
![]()
The characteristic equation corresponding to the variational matrix ![]() is given by
is given by
![]() , (17)
, (17)
where
![]()
According to Routh-Hurwitz criterion, equilibrium point ![]() is locally asymptotically stable provided the following conditions are satisfied
is locally asymptotically stable provided the following conditions are satisfied
![]()
The variational matrix ![]() at equilibrium point
at equilibrium point ![]() is given by
is given by
![]()
where
![]()
The variational matrix ![]() has four eigenvalues. The sign of three eigenvalues b22, b23 and b44 are negative so the stability of equilibrium point E2 depends on sign of b11. The equilibrium point E2 is stable manifold in
has four eigenvalues. The sign of three eigenvalues b22, b23 and b44 are negative so the stability of equilibrium point E2 depends on sign of b11. The equilibrium point E2 is stable manifold in
![]() plane if
plane if ![]() otherwise it is unstable in
otherwise it is unstable in ![]() plane.
plane.
The variational matrix ![]() at equilibrium point
at equilibrium point ![]() is given by
is given by
![]()
where
![]()
The characteristic equation corresponding to the variational matrix ![]() is given by
is given by
![]() , (18)
, (18)
where
![]()
According to Routh-Hurwitz criterion, equilibrium point ![]() is locally asymptotically stable provided the following conditions are satisfied
is locally asymptotically stable provided the following conditions are satisfied
![]() .
.
2.2. Local Stability Analysis with Delay, (i.e.![]() )
)
To discuss the stability behavior of equilibrium ![]() of system (4) with time delay, (i.e.
of system (4) with time delay, (i.e.![]() ), we linearize system (4) by using the following transformations:
), we linearize system (4) by using the following transformations:
![]()
where ![]() and
and ![]() are small perturbations around the equilibrium
are small perturbations around the equilibrium![]() .
.
The linearized system of system (4) about ![]() is given by:
is given by:
![]() (19)
(19)
where![]() ,
,
![]()
and
![]()
The characteristic equation for linearized system (19) is obtained as:
![]() (20)
(20)
where
![]() ,
,
![]()
![]()
![]()
![]()
Let ![]() be one such root. Substituting this in Equation (20) and equating real and imaginary parts, we get
be one such root. Substituting this in Equation (20) and equating real and imaginary parts, we get
![]() , (21)
, (21)
![]() . (22)
. (22)
Squaring and adding Equations (21) and (22), we get
![]() , (23)
, (23)
where
![]() .
.
Substituting ![]() Equation (23) becomes
Equation (23) becomes
![]() , (24)
, (24)
![]() .
.
We assume that:
(H1): ![]()
We notice that ![]() is continuous everywhere with
is continuous everywhere with ![]() when condition (H1) holds and
when condition (H1) holds and![]() . Therefore, the Equation (24) always has at least one positive root. Consequently, the stability criteria of the system for
. Therefore, the Equation (24) always has at least one positive root. Consequently, the stability criteria of the system for ![]() will not necessarily ensure the stability of the system for
will not necessarily ensure the stability of the system for![]() . We assume the Equation (24) has four positive roots denoted by
. We assume the Equation (24) has four positive roots denoted by ![]() denoted as:
denoted as:
![]() .
.
Again solving (21) and (22), we get a critical value of delay given as follows
![]() .
.
2.2.1. Hopf Bifurcation
To investigate the behavior of the system (4) in the neighborhood of![]() . We represent the following theorem.
. We represent the following theorem.
Theorem:
We observe that the conditions for Hopf bifurcation are satisfied yielding the required periodic solution, that is,
![]() .
.
This signifies that there exists at least one eigenvalue with positive real part for![]() .
.
Proof:
Differentiating Equation (20) with respect to![]() , we obtain
, we obtain
![]() . (25)
. (25)
Therefore
![]() (26)
(26)
We can obtain here
![]() . (27)
. (27)
Verifying numerically it has been obtained that the transversality condition holds and hence Hopf bifurcation occurs at![]() .
.
2.2.2. Stability and Direction of Periodic Solutions
In this section, we will derive explicit formulae for determining the direction, stability and period of the bifurcating periodic solutions arises through Hopf bifurcation. The method we will follow is based on the normal form theory and center manifold theorem as given in [10] . Without loss of generality we denote any of the critical values of ![]() by
by ![]() at which Equation (20) has a pair of purely imaginary roots
at which Equation (20) has a pair of purely imaginary roots ![]() and system undergoes Hopf bifurcation. Hence for any root of Equation (20) of the form
and system undergoes Hopf bifurcation. Hence for any root of Equation (20) of the form![]() ,
, ![]() ,
,
![]() and
and![]() . Let
. Let![]() ,
, ![]() , so that
, so that ![]() is Hopf bifurcation value for the system. Define the space of continuous real valued functions as
is Hopf bifurcation value for the system. Define the space of continuous real valued functions as![]() . Using the transformation
. Using the transformation
![]() ,
, ![]() ,
, ![]() and
and ![]() and
and ![]() for
for ![]() ; the delay model system (4), then transform to FDE in
; the delay model system (4), then transform to FDE in ![]() as,
as,
![]() (28)
(28)
where![]() ,
, ![]() ,
, ![]() and
and ![]() and
and ![]() are given by
are given by
![]() (29)
(29)
and
![]() (30)
(30)
where
![]()
![]() ,
,
![]() ,
,
![]() .
.
For![]() .
.
By the Reisz representation theorem there exists a function ![]() whose components are of bounded variation for
whose components are of bounded variation for ![]() such that
such that
![]() . (31)
. (31)
In view of Equation (29) we can choose
![]() , (32)
, (32)
where![]() , define
, define
![]() (33)
(33)
and
![]() (34)
(34)
The system (28) is the equivalent to
![]() , (35)
, (35)
where ![]() for
for![]() .
.
For![]() , define
, define
![]() (36)
(36)
and a bilinear inner product
![]() (37)
(37)
where![]() . Then
. Then ![]() (from here onwards we shall refer
(from here onwards we shall refer ![]() by
by![]() ) and
) and ![]() are adjoint operators. We know that
are adjoint operators. We know that ![]() are the eigenvalues of
are the eigenvalues of![]() . Thus, they are also eigenvalues of
. Thus, they are also eigenvalues of![]() . We need to compute eigenvectors of
. We need to compute eigenvectors of ![]() and
and ![]() corresponding to
corresponding to ![]() and
and ![]() respectively.
respectively.
Suppose ![]() be the eigenvector of
be the eigenvector of ![]() corresponding to eigenvalues
corresponding to eigenvalues ![]() then
then
![]() , (38)
, (38)
which for![]() , gives
, gives
![]() (39)
(39)
Solving the system of Equation (39), we get
![]()
and![]() .
.
Similarly calculating ![]() such that
such that
![]() , (40)
, (40)
where
![]() ,
,
![]() .
.
Now the normalization condition gives
![]() ,
,
![]()
![]() .
.
Thus, ![]() is so chosen such that
is so chosen such that
![]() (41)
(41)
Proceeding same as [10] and using same notation, we compute the coordinates to describe the center manifold ![]() at
at![]() . Let
. Let ![]() be solution of Equation (35) when
be solution of Equation (35) when![]() . Define
. Define
![]() (42)
(42)
On the center manifold![]() , we have
, we have
![]() (43)
(43)
![]() (44)
(44)
![]() and
and ![]() are local coordinates for center manifold
are local coordinates for center manifold ![]() in the direction of
in the direction of ![]() and
and![]() . Note that
. Note that ![]() is real if
is real if ![]() is real. We only consider real solutions. For solution
is real. We only consider real solutions. For solution ![]() of Equation (35). Since
of Equation (35). Since![]() , we have
, we have
![]() (45)
(45)
We rewrite this equation as
![]() , (46)
, (46)
where
![]() (47)
(47)
It follows from (42) and (44) that
![]() , (48)
, (48)
![]() (49)
(49)
Also we have
![]()
where
![]()
![]()
![]() .
.
So that
![]()
![]()
![]()
![]()
Thus
![]()
![]()
![]()
![]()
Now
![]()
Comparing the coefficients in (37) with those in (50), we get
![]()
![]()
![]()
![]()
In order to compute![]() , we need to
, we need to ![]() and
and![]() . From Equations (42) and (45) we have
. From Equations (42) and (45) we have
![]()
![]() (51)
(51)
![]() (52)
(52)
with
![]() (53)
(53)
Also, on![]() , using chain rule, we get
, using chain rule, we get
![]() (54)
(54)
It follows from (46), (52) and (54)
![]() , (55)
, (55)
![]() (56)
(56)
etc. Now for ![]()
![]() (57)
(57)
which on comparing the coefficients with (53) gives
![]() , (58)
, (58)
![]() (59)
(59)
From (56), (58) and the definition of![]() , we have
, we have
![]() . (60)
. (60)
Note that![]() , hence
, hence
![]() (61)
(61)
Similarly from (56), (59) and the definition of![]() , we have
, we have
![]() (62)
(62)
![]() (63)
(63)
where ![]() and
and ![]() are constant vectors, to be determined.
are constant vectors, to be determined.
It follows from the definition of ![]() and (45) that
and (45) that
![]() (64)
(64)
![]() (65)
(65)
From Equations (61) and (63) we get
![]() , (66)
, (66)
and
![]() (67)
(67)
Using (61) and (66) in (64) and noting that ![]() is eigenvector of
is eigenvector of![]() , we have
, we have
![]() (68)
(68)
i.e.
![]() (69)
(69)
Similarly using (63) and (67) in (65), we get
![]() (70)
(70)
We solve system (69) for ![]() and (70) for
and (70) for ![]() and using these values are determine
and using these values are determine ![]() and
and ![]() and hence
and hence![]() . Now to determine the direction, stability and period of bifurcating periodic solutions from critical point at the critical value
. Now to determine the direction, stability and period of bifurcating periodic solutions from critical point at the critical value ![]() we can compute the following necessary quantities as given by [10] .
we can compute the following necessary quantities as given by [10] .
![]() (71)
(71)
![]() (72)
(72)
![]() (73)
(73)
![]() (74)
(74)
Hence, using the results of [10] . We have the following theorem.
Theorem (3.2.1): If![]() , then the Hopf bifurcation is supercritical (subcritical) and the bifurcat-
, then the Hopf bifurcation is supercritical (subcritical) and the bifurcat-
ing periodic solutions exist for![]() . The bifurcating periodic solution is stable (unstable) if
. The bifurcating periodic solution is stable (unstable) if
![]() and the period increase (decrease) if
and the period increase (decrease) if![]() .
.
3. Numerical Support
In this section, we present numerical simulation to illustrate the results obtained in the previous sections. The system (4) is solved using the MATLAB software package under the following set of parameters.
(a)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , , , ,.
, , , ,.
The interior equilibrium point of system (4) with data (a) is
![]()
Then, we can easily obtain that (H1) to be satisfied. By computation, we have ![]()
![]()
![]() . The transversality condition (27) is satisfied as
. The transversality condition (27) is satisfied as![]() .
.
The stability behavior of the system (4) for ![]() can be depicted by Figure 1. To check the dynamic behavior of the system (4) for
can be depicted by Figure 1. To check the dynamic behavior of the system (4) for ![]() can be seen by Figure 2 and Figure 3. A Hopf bifurcation occurs at
can be seen by Figure 2 and Figure 3. A Hopf bifurcation occurs at ![]() when
when ![]() and small amplitude periodic solution around
and small amplitude periodic solution around ![]() and this can be visualized from Figure 2 and Figure 3. From Figure 2 and Figure 3 we can see that when
and this can be visualized from Figure 2 and Figure 3. From Figure 2 and Figure 3 we can see that when ![]() the system is stable and for
the system is stable and for ![]() the system becomes unstable. An alter- native resource has a strong impact on the depletion of forestry biomass which can be seen from Figure 4. From this we can see increasing the value of alternative resource the concentration of forestry biomass increases and also controlling the instability of the system (4) when
the system becomes unstable. An alter- native resource has a strong impact on the depletion of forestry biomass which can be seen from Figure 4. From this we can see increasing the value of alternative resource the concentration of forestry biomass increases and also controlling the instability of the system (4) when ![]() see Figure 4(b). Now see impact of other factors on forestry biomass. Increasing the value of
see Figure 4(b). Now see impact of other factors on forestry biomass. Increasing the value of ![]() the concentration of forest biomass increases
the concentration of forest biomass increases
![]() (a)
(a)![]() (b)
(b)
Figure 2. Trajectory portrait and phase portrait of system (4) for ![]() and other parameters are same as (a).
and other parameters are same as (a).
refer Figure 5. From Figure 6 we see that the concentration of forestry biomass decreases when the value of ![]() increases. Increasing the values of
increases. Increasing the values of ![]() and
and ![]() the concentration of forestry biomass increases refer Figure 7 and Figure 8.
the concentration of forestry biomass increases refer Figure 7 and Figure 8.
Now to verify the result of Theorem (3.2.1), we have shown the variation of variables ![]() and
and ![]() for
for ![]() and
and ![]() in Figure 2 and Figure 3 respectively. Also for the above set of parameter values, we get
in Figure 2 and Figure 3 respectively. Also for the above set of parameter values, we get
![]() ,
, ![]() ,
, ![]() and
and![]() . Since
. Since![]() , the Hopf bifurcation is supercritical and the direction of the bifurcation
, the Hopf bifurcation is supercritical and the direction of the bifurcation![]() . Also
. Also ![]() and
and![]() , this implies
, this implies
that the bifurcating periodic solutions arising from ![]() at
at ![]() are stable and the periods of limit cycle increases.
are stable and the periods of limit cycle increases.
![]() (a)
(a)![]() (b)
(b)
Figure 3. Trajectory portrait and phase portrait of system (4) for ![]() and other parameters are same as (a).
and other parameters are same as (a).
4. Conclusion
In this paper, a nonlinear mathematical model is proposed and analyzed to see the effect of alternative resource and time delay on conservation of forestry biomass. We have obtained the explicit formulae that determine the stability and direction of the bifurcating periodic solutions by using the normal form theory and the center manifold theorem. For the given set of parameter values in (a), we found that, the Hopf bifurcation was supercritical with stable periodic solutions and the direction of bifurcation was![]() . Forests serve as a source of life for the forest based small and large scale industries. However, due to shrinking forests area, the industries are facing wood crisis. To overcome wood crisis, alternative resources like synthetic, liquid wood, plastic, wood composite lumber etc are good alternative for wood based products. For preserving our forestry biomass we can control the
. Forests serve as a source of life for the forest based small and large scale industries. However, due to shrinking forests area, the industries are facing wood crisis. To overcome wood crisis, alternative resources like synthetic, liquid wood, plastic, wood composite lumber etc are good alternative for wood based products. For preserving our forestry biomass we can control the
![]()
Figure 5. Variation of the forestry biomass with time for different values of ![]() and other parameter values are same as (a).
and other parameter values are same as (a).
![]()
Figure 6. Variation of the forestry biomass with time for different values of γ1 and other parameter values are same as (a).
![]()
Figure 7. Variation of the forestry biomass with time for different values of ϕ and other parameter values are same as (a).
![]()
Figure 8. Variation of the forestry biomass with time for different values of ϕ1 and other parameter values are same as (a).
wood based industries by human awareness or some government action. Hence, we conclude from our analysis that the forestry biomass may be conserved by applying technological effort and alternative resources.
Acknowledgements
Second author thankfully acknowledges the NBHM (2/40(29)/2014/R&D-11/14138) for the financial assistance in the form of PDF.