A Heuristic Algorithm for Vehicle Routing Problems with Simultaneous Pick-Up and Delivery and Hard Time Windows ()
1. Introduction
The problems concerning the distribution of goods between depots and final users are known as Vehicle Routing Problems (VRPs). Vehicle routing problems are widespread in distribution and logistics [1]. The general VRP comprised an assignment problem, travelling salesman problem and vehicle-path problem [2]. Dantzig and Ramser introduced VRP in 1959, and described a real world application, and proposed the first mathematical programming formulation and algorithmic approach for the solution of the problem [3].
The basic VRP involves a central depot, a set of customers requiring delivery of goods from the depot, and a fleet of identical vehicles located at the depot. The objective of VRP is to minimize the total traveled distance, traveling cost or the number of vehicles used to serve all customers. In the field of combinatorial optimization, the VRP is regarded as NP-hard. Several classes of VRPs, which are extensions of basic VRP, have been studied in the literature. Details and literature of VRP and its variants are given by [4] and [5].
The sub-class of VRP in which customers ask for delivery in a specified time window [a, b] is referred to as vehicle routing problem with time windows constraints (VRPTW) [6]. Time windows characterize the earliest (ai) and the latest (bi) allowable times that the service should begin within. A vehicle is permitted to arrive earlier than ai to a customer i, in which case it will wait until service begins at time ai. Late arrivals, i.e. arrivals after bi, are not permitted. The problems considering this type of time windows are called as vehicle routing problems with hard time windows (VRPHTW). On the other hand, both lower and upper bounds of time windows need not be met, but can be violated. These problems are known as vehicle routing problems with soft time windows (VRPSTW) [7]. Additionally, the total duration of any route (traveling time + service time) cannot exceed the pre-determined route duration. Salversberg proved that the VRPTW is an NP problem [8]. Typical applications of the VRPTW include bank deliveries, school bus routing, postal deliveries [9]-[11]. The early work on VRPTW are generally case study oriented [12]-[14]. Later, researchers focused their attention on the development of effective optimal approaches and the design of heuristics for solving realistic-size problems. Detailed studies about VRP and VRPTW are [10] [11] [15] [16].
An extension of basic VRP is vehicle routing problems with pickup and delivery (VRPPD). In VRPPD, every customer has 2 two types of demand such as pick up demand (pi) and delivery demand (di). Delivery demand refers to the amount of goods transported from depot to customer; pickup demand refers to the amount of goods transported from customer to depot. VRPPD is classified into 3 groups considering the dealing with delivery and pick up demand aspects as follows:
Delivery first- pickup second VRPPD: Customers are visited more than once. First, goods are transported from depot to the customers; then, from customers to depot. There is precedence between delivery and pick up customers.
Mixed pickups and deliveries VRPPD: There is not precedence between delivery and pick up. Delivery demand and pick up demand is serviced in a mixed sequence. Customers are visited more than once.
Simultaneous pickups and deliveries VRPPD: Delivery and pick up demand are serviced simultaneously. This type of problem is specifically denoted as VRPSPD. Customers are visited only once.
VRPSPD is encountered in real life. For example, in the soft drink industry full bottles are transported from depot to markets, empty bottles are returned back to the depots and in the grocery industry goods flow from depot to market while outdated products flow to depots. VRPSPD is an NP-hard combinatorial optimization problem because it is a version of VRP [17]. Min introduced VRPSPD and proposed an algorithm for transportation of books between libraries where there is one depot, and there are 2 vehicles and 22 customers [18]. That algorithm is based on cluster first-route second approach. Dethloff proposed a mathematical formulation for the problem and also developed an insertion-based heuristic to solve the problem [19]. In literature, mathematical model for VRPSPD İS proposed 29 by [18]-[23]. Ropke and Pisinger developed a unified model capable of handling most variants of the problem from the literature [24]. Bianchess and Righini presented and compared the performance of constructive algorithms, local search and tabu search algorithms [25]. Tang Montane proposed a mathematical formulation and a tabu search algorithm, which is intensified and diversified by the use of frequency penalization scheme for VRPSPD [26]. Zachariadis et al. proposed a hybrid meta-heuristic approach based on tabu search and guided local search [17]. Gajpal and Abad presented an ant colony system algorithm for VRPSPD [27]. Ai and Kachitvchyanukul proposed a mathematical formulation and a particle swarm optimization algorithm for VRPSPD [23]. The formulation is generalization of mathematical formulations proposed by Min [18], Dethloff [19], and Tang Montane et al. [26]. Chen et al. proposed a hybrid meta-heuristic method based on record to record travel tabu list and route improvement routines [28]. Zachariadis et al. presented an adaptive memory programming methodology algorithm for the VRPSPD [17]. Angellini and Mansini developed a branch and price algorithm for VRPSPDTW [29]. Mingyong and Erbao (2010) proposed an improved differential evolution algorithm (IDE) for solving VRPSPDTW [30]. Unlike the work of Angellini and Mingyong, in this study, the objective in determined problems is to minimize the simultaneous pick up and hard time windows and arp objective function waits. Mathematical model was specified and heuristic algorithm for the solution was developed.
2. Problem Description and Notation
We propose a mathematical formulation and develop a heuristic algorithm for the VRPSPDHTW. Proposed problem is NP-hard as it is the extension of VRPSPD and VRPTW. The proposed mathematical model is based on Dethloff’s mathematical model where time windows are inserted and objective function is considered as the minimization of total waiting time.
VRPSPDHTW can be formally defined as follows. Let G = (V, A) is a graph where 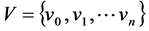 is a vertex set, and
is a vertex set, and 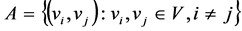 is an arc set. Vertex v0 represents the depot and vertex vi repre- sents the customers where i = 1,…,n. Every customer has a nonnegative pick up quantity pi, delivery quantity di, and service time si. Each vehicle has a capacity of Q. The goal of VRPSPDHTW is to determine a set of routes that satisfy the following requirements [32]:
is an arc set. Vertex v0 represents the depot and vertex vi repre- sents the customers where i = 1,…,n. Every customer has a nonnegative pick up quantity pi, delivery quantity di, and service time si. Each vehicle has a capacity of Q. The goal of VRPSPDHTW is to determine a set of routes that satisfy the following requirements [32]:
1) Each route starts and ends at the depot,
2) Each customer is serviced exactly once by exactly one vehicle,
3) All customer delivery and pick up demand are totally satisfied in the related time interval (a vehicle is permitted to arrive earlier than ai to a customer but not permitted to arrive later than bi)
4) Total vehicle load through any route does not exceed the vehicle capacity Q,
5) Homogeneous fleet of vehicles exists in the depot.
6) Total waiting time is minimized.
Notations and parameters used in the model are given as:
J: Set of all customer locations
J0: Set of all nodes, i.e. customer locations and depot
V: Set of all vehicles
C: Vehicle capacity
tij: Travel time between nodes
si: Service time
Zij: Addition of service time and travel time between nodes (Zij = si + tij)
Wiv: Starting time of service at node i by vehicle v
Viv: Arrival time at node i by vehicle v
Dj: Delivery amount of customer j
N: Number of nodes,
Pj: Pick up amount of customer,
M: A large number
ai: The earliest starting time of service at node i
bi: The latest starting time of service at node i
Decision Variables:
lv’: Load of vehicle v when leaving the depot,
lj: Load of vehicle v after having serviced customer j,
πj: Variable used to prohibit sub tours,
Xijv = binary variable indicating where vehicle v travels directly from node i to node j (xijv = 1)
or not (xijv = 0)
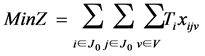 (1)
(1)
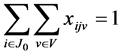 j = 1, 2, ..., J (2)
j = 1, 2, ..., J (2)
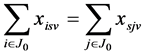 v = 1, 2, ..., V (3)
v = 1, 2, ..., V (3)
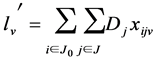 v = 1, 2, ..., V (4)
v = 1, 2, ..., V (4)
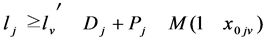 v = 1, 2, ..., V ; j = 1, 2, ..., J (5)
v = 1, 2, ..., V ; j = 1, 2, ..., J (5)
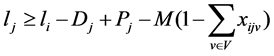 i, j = 0, 1, 2, ..., J (6)
i, j = 0, 1, 2, ..., J (6)
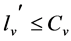 v = 1, 2, ..., V (7) and
v = 1, 2, ..., V (7) and 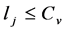 v = 1, 2, ..., V; j = 1, 2, ..., J (8)
v = 1, 2, ..., V; j = 1, 2, ..., J (8)
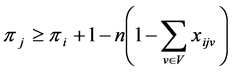 j = 1, 2, ..., J; i = 1, 2, ..., J (9)
j = 1, 2, ..., J; i = 1, 2, ..., J (9)
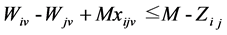 i, j = 0, 1, 2, ..., J; v = 1, 2, ..., V (10)
i, j = 0, 1, 2, ..., J; v = 1, 2, ..., V (10)
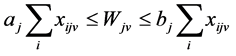 i, j = 0, 1, 2, ..., J; v = 1, 2, ..., V (11)
i, j = 0, 1, 2, ..., J; v = 1, 2, ..., V (11)
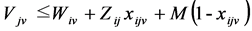 i, j = 0, 1, 2, ..., J; v = 1, 2, ..., V (12)
i, j = 0, 1, 2, ..., J; v = 1, 2, ..., V (12)

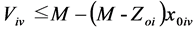 j = 0, 1, 2, ..., J; v = 1, 2, ..., V (13)
j = 0, 1, 2, ..., J; v = 1, 2, ..., V (13)
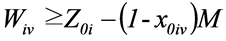 j = 0, 1, 2, ..., J; v = 1, 2, ..., V (14)
j = 0, 1, 2, ..., J; v = 1, 2, ..., V (14)
![]() i = 0, 1, 2, ..., J; v = 1, 2, ..., V (15)
i = 0, 1, 2, ..., J; v = 1, 2, ..., V (15)
![]() j = 0, 1, 2, ..., J; v = 1, 2, ..., V (16)
j = 0, 1, 2, ..., J; v = 1, 2, ..., V (16)
![]() j = 1,2,…,J (17)
j = 1,2,…,J (17)
and ![]() j = 1, 2 ,..., J; i = 1, 2, ..., J; v = 1, 2, ...,V (18)
j = 1, 2 ,..., J; i = 1, 2, ..., J; v = 1, 2, ...,V (18)
In the model; the objective function (1) minimizes the waiting times between the nodes, constraint (2) states that every customer node must be serviced exactly once, constraint (3) states that each customer must be serviced with the same vehicle. Constraint (4) gives the initial vehicle load, constraint (5) is the vehicle load after first customer, and constraint (6) is the vehicle load ‘en route’. Constraint (7) and (8) compare vehicle load and vehicle capacity after first customer and ‘en route’. Constraint (9) is a sub tour breaking constraint. Constraint (10) determines the starting time of service at all nodes through the route and constraint (11) assures that the starting time of service is between the time intervals. Constraint (12) and (13) determine the arrival time to any node through the route, and arrival time to the first node after the depot, respectively. Constraint (14) determines the starting time of service at the first node after the depot. Constraint (15) assures that the service will start after the vehicle arrives to the node, constraint (16) determines the waiting time. Constraint (17) and (18) describe the domain of decision variables: πj are non- negative variables, and xijv are binary variables.
3. A Heuristic for VRPSPDHTW
Due to the results of test problems solved using the mathematical model proposed above, it is clearly determined that this approach is not capable of yielding good results in a reasonable time for bigger sized test problems. In order to solve bigger sized problems, a heuristic approach is proposed in this paper. The step by step flow of the heuristic is given below:
1) Open a list of nodes L and sort them by increasing values of the earliest starting time of service ai. If several nodes have the same ai, sort them by increasing values of the latest starting time of service bi.
2) Pick up the top node i on the list L and place it at the bottom of list K, then delete node i from the list L and calculate I0 and Iq:
![]()
![]() (19)
(19)
3) Calculate RD and RP values for nodes at list K where RD (q) stands for the residual delivery capacity, and RP (q) stands for the residual pick up capacity at the depot
![]()
![]() (20)
(20)
![]()
![]()
4) Verify that the following formulation for nodes in list L is satisfied,
![]() and
and ![]() (21)
(21)
If it is satisfied, this means that node u can be placed after node i. If not, node u cannot be placed after node i, which means that it is infeasible.
5) Place the nodes that satisfy step 4 at list L’, if L’ = Ǿ close list K and return to step 2.
6) Calculate Wik and Vjk values for nodes at List L’ (Vjk, the arrival time at node j by vehicle k; Fik, the departure time from node i by vehicle k)
i = 0 F0k = 0 ![]() and Vjk = Fik + ti (22)
and Vjk = Fik + ti (22)
If Vik > bi for all nodes at list L’ then close list K, return to step 2.
7) Calculate the waiting times as
![]() (23)
(23)
8) If Fnk + tn0 > b0 (this means; the time to return to the depot is bigger than the latest starting time of service for depot), it is infeasible. If all nodes on list K’ satisfy this condition, return to step 2
9) Choose the node that has smallest Wi and place on list K, delete the node from list L,return to step 2.
10) If List L is empty, stop the algorithm.
In order to investigate the performance of the mathematical model [31] and heuristic algorithm [32] proposed here, test problems with 5, 7, 10, 15 and 20 customers are solved. The main idea of choosing these problems is that for test problems with more customers the mathematical model cannot produce an optimal solution in a reasonable time period which is considered to be 7200 seconds in this study. The original test problems of Solomon includes 100 customers in each of the cases, satisfying the constraints in our case and the total capacity of the vehicles are determined to be half of its original value.
4. Numerical Examples
Since VRR_SPD_HTW has never been solved before, there is no data to test VRRSPDHTW in the literature. For this reason, Solomon’s data is modified in order to be used in our algorithm. A full description of Solomon’s problems can be found in Solomon [10]. Solomon’s problems are grouped into 3 categories: C, R, and RC. Every category has 8 to 12 examples. Each example has a depot and 100 customers. Every category is classified into 2 groups as Type 1 and Type 2. The differences between Type1 problems and Type 2 problems are vehicle capacity and time windows. Type 1 problems have narrow time windows and small vehicle capacity while Type 2 problems have wide time windows and large vehicle capacity. The locations of customers are uniformly distributed in R1 and R2, and clustered in C1 and C2. For groups RC1 and RC2, the clustered and random distributions are mixed.
We use Salhi and Nagy’s [20] formulations to modify Solomon’s data. In order to investigate the effectiveness of both the mathematical model and the heuristic, test problems with 5, 7, 10, 15 and 20 customers are generated. The original test problems of Solomon includes 100 customers in each of the cases and in order to satisfy the constraints, the total capacity of the vehicles are determined to be half of its original value. The mathematical model is solved using a personal computer with a microprocessor with 2.6 Ghz and under 1 Gb Ram using GAMS package with a time limit of 7200 seconds. The solutions with the heuristic were calculated at the same computer using MATLAB coding language. The objective in determined problem is the minimization of the waiting times. The objective is, therefore, to expect the function take a value between 0 and + infinite. If in any problem the optimum solution value is z = 0, then it means that service is provided to the customers without making them wait. In comparing the results of mathematical model and heuristic algorithm, CPU average and Deviation average were used depending on the problem type. CPU average and Deviation average were calculated by dividing the sum of CPU and Deviation values into the number of the problems for every problem. Deviation values stand for the distance of z value of related problem in terms of percentage to the best z value. These values were calculated according to the given formula below:
Deviation MM = ((MMresult − min(MMresult,SAresult)/MMresult)*100 (24)
DeviationSA = ((SAresult − min((MMresult,SAresult)/SAresult)*100
In this formula, MMresult represents MMathematical model results and SA result represents the results of heuristic algorithm. The obtained CPU and Deviation averages depending on the problem type can be seen in Cetin’s desirtation [32] The Deviation Average = 0 in tables means that the related method gives the best result in all the problem types. Being different from zero gives how far it is from the best solution on average as percentage. In large-sized sample problem, heuristic algorithm gives better results when compared to mathematical model. This can be seen in Cetin’s desirtation also [32].
5. Conclusion
In this study, VRPSPDHTW is determined. For the determined problem, mathematical model and heuristic algorithm aiming to minimize the waiting times are developed. For sample groups with 5, 7, 10, 15 and 20 customers are examined. The demand of Solomon’s Data are modified to get pickup and delivery demand. 112 problems were solved for each sample customer group. The results of mathematical model and heuristic algorithm were compared for sample groups by calculating deviation values depending on the problem type. When the results are analyzed, it was seen that heuristic algorithm obtains values very close to mathematical model in small-sized problems. In large-sized problems, however, it was observed that heuristic algorithm gives better results when compared to mathematical model. Moreover, it was observed that in problems where mathematical model cannot reach a solution, heuristic model reaches solution.
NOTES
*Corresponding author.