Impact Factor Dynamic Forecasting Model for Management Science Journals Based on Grey System Theory ()
1. Introduction
Journal Citation Reports (JCR) issued by American Information Research Institute (ISI) is an authoritative system for evaluating journals. This paper is based on JCR database and grey system theory, building a trend analysis method for the average impact factor (IF) of the top 20 management science journals. The results can provide reference for related researchers.
2. Theory and Methods
Grey system theory [1] was based on the macro forecast and decision about society and economy when it was earliest proposed. And GM (1, 1) model was one of the most widely used grey models. Setting time series as t = {t1, t2,∙∙∙, tn}, the corresponding original data sequence is
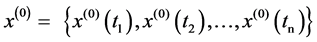 (1)
(1)
Setting ?tk = tk − tk-1, when ?tk = const, sequence (1) is equal-space sequence. When ?tk ≠ const, sequence (1) is non-equal-space sequence. One-accumulated generate sequence of original data sequence (1) is x (1) = {x (1) (t1), x (1) (t2), ∙∙∙, x (1) (tn)}, wherein
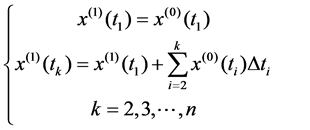 (2)
(2)
Calculation formulas for reverting one-accumulated generate sequence to original sequence (1) is
 (3)
(3)
When one-accumulated generate sequence was close to nonhomogeneous exponential law change, the response function was the solution of differential Equation (4).
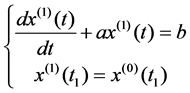 (4)
(4)
The solution was
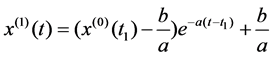 ,
,
in which unknown constants a and b were uncertain parameters. Discrete response function of (4) was
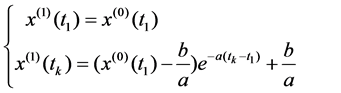 (5)
(5)
In Equation (5), k = 2, 3, ∙∙∙, n. To determine uncertain parameters a and b, we could use difference Equation (4).
 (6)
(6)
wherein
 ,
,
with z (1) (tk) = λx(1) (tk)+ (1 − λ) (1) (tk − 1) smoothing x(1) (tk) of difference Equation (6), we could get difference equation
 (7)
(7)
In above formula, z(1) (tk) was called as background value and l ∈ [0, 1] was called as background parameters. At present, there is still no optimum getter for background parameters l, in order to be used simply and easily, we generally take background parameters for 1/2 in reference [1]. Substituting one-accumulated generate sequence of original sequence (1) into above formula, with matrix equation a and b could be [a b]T = (BTB)−1BTY determined, inside Y = [x(0) (t2), x(0) (t3), ∙∙∙, x(0) (tn)]T, and
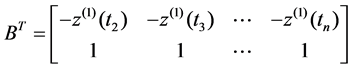 .
.
Substituting obtained parameters a and b into Equation (5), we could get GM (1.1) model of sequence x(0):
 (8)
(8)
The traditional modeling method of GM (1.1) model had the advantages of simple computation, but its fitting and forecast precision sometimes was poor. Integrating solving parameters and determining boundary value together to discuss in [2] and [3], we put forward a method based on information mining. GM (1.1) model with this modeling method both can greatly improve the fitting and prediction precision of GM (1.1) model, and keep the advantage of simple computation in the traditional modeling method of GM (1.1) model. For the convenience of the reader, the following is a brief introduction of this method. Firstly, by using the modeling method of traditional grey system GM (1.1) model, we got grey system GM (1.1) model (8) of original sequence x(0), then we could call model (8) as rough model. Finish machining of rough model (8) namely rewrote third formulas of rough model (8) as follow, where in, a and b were new uncertain parameters.
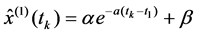 k = 2, 3, ∙∙∙, n (9)
k = 2, 3, ∙∙∙, n (9)
By using the modeling method of traditional grey system GM (1.1) model, parameters a could be gotten, then using the accumulated generate sequence and corresponding time series of original sequence again. Substituting the accumulated generate sequence x (1) = {x(1) (t1), x(1) (t2), ∙∙∙, x(1) (tn)} and corresponding time series of original sequence t = {t1, t2, ∙∙∙, tn} into above formula, we could determine uncertain parameters a and b with matrix equation [4] [a b]T = (B TB)−1B TY, inside Y = [ x(1) (t1), x(1) (t2), ∙∙∙, x(1) ( tn)]T and
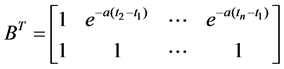 .
.
Substituting parameters a and b into Equation (9), we got new GM (1.1) model of original sequence x(0):
 k = 1, 2, ∙∙∙, n (10)
k = 1, 2, ∙∙∙, n (10)
One-inverse accumulated generating above formula, we could get the reducing value of original sequence x(0)
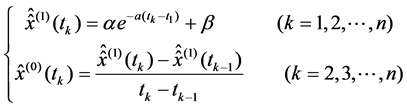 (11)
(11)
3. Impact Factor Dynamic Forecasting Model GM (1.1)
With original data, firstly, modeling GM (1.1) model by using grey system theory; then, on the basis of construction grey system GM (1.1) model, we constructed GM (1.1) model based on information mining.
Table 1 shows the statistical number of the average impact factor (IF) of the top 20 management science journals from 2004 to 2013. Data came from web of science.
The grey system GM (1, 1) model based on information mining method as follow, wherein k = 1, 2, ∙∙∙, and n.
 (12)
(12)
Figure 1 is a diagram of the curve of original data and its simulation data from 2004 to 2013.
From 2004 to 2013 the number of the average impact factor (IF) over time trend graph can be seen that the number of the average impact factor (IF) is gradually slowly increase trend.
Based on GM (1, 1) model (12), we forecasted the number of the average impact factor (IF) form 2014 to 2019. Results showed a slowly increase trend. Specific data are shown in Table 2.
![]()
Figure 1. The tendency curve of the average impact factor with time.
4. Conclusion
This paper gives a modeling way based on information mining and grey system theory. On the one hand, this way greatly improved GM (1, 1) model’s fitting precision and prediction accuracy; on the other hand, it maintains the advantage of the traditional modeling method which is simple. The grey system GM (1, 1) model of impact factor (IF) trend was constructed. The model evaluates and predicts the average impact factor (IF) trend of the top 20 management science journals. Case analysis verified the validity and usefulness of the information mining method. The results can provide reference for related researchers.
NOTES
*Corresponding author.