Hydrodynamic Interactions Introduce Differences in the Behaviour of a Ratchet Dimer Brownian Motor ()
1. Introduction
Brownian motors are small physical micro- or even nano-machines that operate far from thermal equilibrium by extracting the energy from both thermal and non-equilibrium fluctuations in order to generate work against external loads. They present the physical analogue of bio-molecular motors that also work out of equilibrium to direct intracellular transport and to control motion in cells. In such bio-molecular motors, proteins such as kinesins, myosins and dyneins, move unidirectionally on one-dimensional “tracks” while hydrolysing adenosine triphosphate (ATP). These molecular motors are powered by a ratchet mechanism [1] ; they convert the nonequilibrium fluctuation into directed flow of Brownian particles in an asymmetrical periodic potential (ratchet) without any net external force or bias. Several authors have studied theoretically the transport of two coupled particles modeling the two heads of a motor protein [2] - [13] . Nonequilibrium fluctuations, whether generated or by a chemical reaction far from equilibrium, can bias the Brownian motion of a particle in an anisotropic medium without thermal gradients, a net force such as gravity, or a macroscopic electric field. Fluctuation-driven transport is one mechanism by which chemical energy can directly drive the motion of particles and macromolecules and may find application in a wide variety of fields, including particle separation and the design of molecular motors and pumps. Zimmermann and Seifert [14] studied the efficiencies of a molecular motor for a generic hybrid model applied to the F1-ATPase, and they obtained good quantitative agreement with the experimental data. Pinkoviezky and Gov [15] were motivated by the observed pulses of backward-moving myosin-X in the filopodia structure, and they modelled interacting molecular motors with an internal degree of freedom, introducing a novel modification to the approximation scheme.
In the present work, we use the Brownian dynamics with hydrodynamic interactions simulation in order to describe the movement of an elastically coupled dimer Brownian motor in a ratchet potential. In Section 2, we describe the forces acting on an oscillating dimer in a ratchet potential with a load force and an external unbiased fluctuation, which acts simultaneously on two particles. In Section 3, we describe the formalism given by Ermak and McCammon (1978) [16] , which couples the forces described in Section 2 and thermal noise with the diffusion tensor. A striking feature of fluid mechanics in the viscously dominated regime, or equivalently, at low Reynolds number, is the long range of hydrodynamic interactions. For example, the Stokeslet, or flow field induced by a point force, falls off inversely with distance. Hydrodynamic interactions have been considered by several authors to explain different phenomena. Kemps and Bhattacharjee, [17] , used a particle tracking model for colloid transport near planar surfaces covered with spherical asperities. This model provides a preliminary step in investigating how geometrically tractable asperities alter the undisturbed flow field and hydrodynamic interactions between the particle and the substrate. Hydrodynamic interactions allow in average for directed motion of a three-sphere system, and the spheres are connected by two identical active linker arms. Each linker arm contains molecular motors and elastic elements and can oscillate spontaneously; see [18] . Microorganisms are often subjected to swimming in close proximity to each other as well as other boundaries. The resulting hydrodynamic interactions may have puzzling effects on their swimming speed, trajectory, and power dissipation. These effects were investigated by Ramia et al. [19] ; each microorganism consisted of a sphere propelled by a rotating helix. It was found that only a small increase (less than 10%) resulted in the mean swimming speed of an organism swimming near and parallel to another identical organism. In a later paper, [20] focused on hydrodynamic interactions by considering two rotating rigid helices. They supposed that the helices were driven by stationary motors, and obtained complementary results to those of Ramia et al., since the hydrodynamic interactions between their helices were stronger. Recently Fornés, [21] , showed that hydrodynamic interactions induced movement against an external load in a ratchet dimer Brownian motor. In the present paper, we show that hydrodynamic interactions introduce differences in the behaviour of a ratchet dimer Brownian motor as compared without them. We report differences in the Peclet number, effective diffusion coefficient, mean 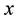 component of the mass center position and velocity and particles positions cross correlations in
component of the mass center position and velocity and particles positions cross correlations in 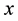 direction.
direction.
2. The Model
We consider an elastically coupled dimer in 3 dimensions in an asymmetrical potential (ratchet) in the 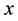 direction, see Figure 1. We considered a linear superposition of three spatial harmonics, following Ref. [22] ,
direction, see Figure 1. We considered a linear superposition of three spatial harmonics, following Ref. [22] ,
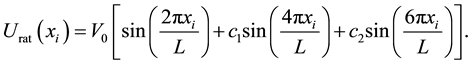 (1)
(1)
The corresponding force on the particles produced by the ratchet potential is given by:
 (2)
(2)
In the former equations 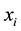 is the
is the 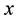 coordinate of particle
coordinate of particle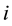 ,
, 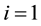 and 2, to distinguish the dimer particles. The parameters
and 2, to distinguish the dimer particles. The parameters 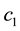 and
and 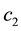 determine the ratchet profile. We use the parameters from Ref. [22] :
determine the ratchet profile. We use the parameters from Ref. [22] :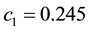 ,
, 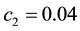 and
and .
.
![]()
Figure 1. Dimer in an assymetrical ratchet potential under a constant load force, thermal noise and unbiased thermal sinusoidal fluctuation.
We define 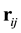 the vector from the center of particle
the vector from the center of particle ![]() to the center of particle
to the center of particle![]() , for particles
, for particles![]() ,
, ![]() , we have
, we have
![]() (3)
(3)
i, j, k are unit vectors in the direction of the cartesian axis, with
![]() (4)
(4)
Then the modulus of the harmonic force is,
![]() (5)
(5)
where ![]() is the strength of the harmonic potential and
is the strength of the harmonic potential and ![]() is the equilibrium position.
is the equilibrium position.
Then the components of the harmonic force are,
![]() (6)
(6)
The corresponding components of the harmonic force on each dimer particle are,
![]() (7)
(7)
Then the forces acting on the dimer particles are:
![]() (8)
(8)
The load force, ![]() , acts to oppose the motors forward progress,
, acts to oppose the motors forward progress, ![]() is an external unbiased fluctuation, which acts simultaneously on two particles.
is an external unbiased fluctuation, which acts simultaneously on two particles.
3. Brownian Dynamics with Hydrodynamic Interactions
Consider a system of N spherical interacting Brownian particles suspended in a hydrodynamic medium, the displacement of particle ![]() during
during ![]() is given by Ermak and McCammon (1978) [16] , namely
is given by Ermak and McCammon (1978) [16] , namely
![]() (9)
(9)
where the superscript “0” indicates that the variable is to be evaluated at the beginning of the time step. ![]() is the force acting on particle
is the force acting on particle![]() .
. ![]() is a random displacement with a Gaussian distribution function whose average value is zero and the correlation is
is a random displacement with a Gaussian distribution function whose average value is zero and the correlation is![]() .
.
![]() (10)
(10)
![]() is the diffusion coefficient of a single subunit sphere of
is the diffusion coefficient of a single subunit sphere of ![]() radius,
radius, ![]() is the dyadic product, for particles
is the dyadic product, for particles![]() ,
, ![]() , we have
, we have
![]() (11)
(11)
In our case of a dimer in three dimensions the tensor ![]() is a
is a ![]() matrix. For details on hydrodynamic interactions see our recent article [21] [23] [24] , also Refs. [25] [26] .
matrix. For details on hydrodynamic interactions see our recent article [21] [23] [24] , also Refs. [25] [26] .
A first basic quantity of interest, in our case, is the average center of mass velocity in the ![]() direction,
direction, ![]() , in the long-time limit, i.e., after transients due to initial conditions have died out, is given by
, in the long-time limit, i.e., after transients due to initial conditions have died out, is given by
![]() (12)
(12)
where![]() .
.
Another quantity of central interest will be the effective diffusion coefficient,
![]() (13)
(13)
where![]() . The means are over the realizations of the stochastic process.
. The means are over the realizations of the stochastic process.
The competition between the drift ![]() and diffusivity
and diffusivity ![]() in advection-diffusion problems is often expressed by a dimensionless number, the Péclet number,
in advection-diffusion problems is often expressed by a dimensionless number, the Péclet number, ![]() , [27] ,
, [27] ,
![]() (14)
(14)
here ![]() is a typical length scale, in our case the length of a single ratchet element,
is a typical length scale, in our case the length of a single ratchet element, ![]() is the average stationary velocity of the particle, in our case we used
is the average stationary velocity of the particle, in our case we used![]() . The larger the Péclet number, the more net drift predominates over diffusion.
. The larger the Péclet number, the more net drift predominates over diffusion.
4. Results
We performed the simulation in dimensionless units. Distance is in units of the separation distance ![]() and time is in units of
and time is in units of![]() , We used in the simulations the following parameters:
, We used in the simulations the following parameters:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , the simulation time was
, the simulation time was![]() , which corresponds to
, which corresponds to ![]() steps. The corresponding dimension units are:
steps. The corresponding dimension units are:![]() ,
, ![]() ,
, ![]() ,
, ![]() Å,
Å, ![]() ,
, ![]() ,
, ![]() ,
,![]() . In Brownian dynamics simulations with hydrodynamic interactions the size of the physically meaningful time step is restricted to values which are sufficiently long
. In Brownian dynamics simulations with hydrodynamic interactions the size of the physically meaningful time step is restricted to values which are sufficiently long![]() . In our case
. In our case ![]() fs where we have used
fs where we have used ![]() Kg for the protein dimer unit of 2.5 Å of radius.
Kg for the protein dimer unit of 2.5 Å of radius.
The average velocity of a molecular motor is a function of the load force resisting the motor’s advancement. One of the characteristic of a molecular motor is the load force-velocity curve. In Figure 2 we show ![]() as a function of the load force
as a function of the load force![]() . Each point of the curve of Figure 2 is the result of 500 stochastic realizations. At the stationary state, the ratio
. Each point of the curve of Figure 2 is the result of 500 stochastic realizations. At the stationary state, the ratio![]() , where
, where ![]() is the standard error of the mean velocity
is the standard error of the mean velocity![]() .
.
In the range ![]() we observe, the motor continue with a positive velocity in spite of the negative load force (motor effect). We also observe a substantially increase of the motor velocity in the case with hydrodynamic interaction as compared without it.
we observe, the motor continue with a positive velocity in spite of the negative load force (motor effect). We also observe a substantially increase of the motor velocity in the case with hydrodynamic interaction as compared without it.
In Figure 3, we observe the behaviour of the mass center position variance, ![]() ,
,
as a function of time in the long time limit, i.e., after transients due to initial conditions have died out. The effective diffusion coefficient is giving by the slope of the linear fitting, ![]() in accordance to Equation (13), we observe greater slope for the case with hydrodynamic interactions.
in accordance to Equation (13), we observe greater slope for the case with hydrodynamic interactions.
In Figure 4 is shown the effective diffusion coefficient as a function of the load force, ![]() vs
vs![]() , we observe that hydrodynamic interactions increase the effective diffusion.
, we observe that hydrodynamic interactions increase the effective diffusion.
![]()
Figure 4. The effective diffusion coefficient as a function of the load force, ![]() vs
vs![]() .
.
In Figure 5 is shown the Péclet number as a function of the load force, ![]() vs
vs![]() , we observe lower Péclet numbers for the case with hydrodynamic interactions, meaning that the net drift diminish over diffusion as compared with the case without hydrodynamic interactions.
, we observe lower Péclet numbers for the case with hydrodynamic interactions, meaning that the net drift diminish over diffusion as compared with the case without hydrodynamic interactions.
![]()
Figure 5. Péclet number as a function of the load force, ![]() versus
versus![]() .
.
In Figure 6 is shown the mean x component of the mass center position as a function of time, ![]() versus
versus
time, in the long-time limit, for a given load force,![]() . We observe a linear relation, with
. We observe a linear relation, with ![]() in the
in the
case with hydrodynamic interactions greater than the case without them.
In Figure 7 we observe the behaviour of the average center of mass velocity in the ![]() direction,
direction, ![]() versus time, in the long-time limit for a given load force,
versus time, in the long-time limit for a given load force,![]() . The velocity is substantially greater for the case with hydrodynamic interactions.
. The velocity is substantially greater for the case with hydrodynamic interactions.
In Figure 8 is shown the spatial cross correlations in x direction as a function of Lag time, ![]() versus Lag time. We observe that the correlation is higher in the case with hydrodynamic interactions.
versus Lag time. We observe that the correlation is higher in the case with hydrodynamic interactions.
A similar result was found by Houtman et al. [28] who developed a simple 2D-lattice model in order to test the influence of hydrodynamic interactions on the collective transport of molecular motors, which is important for the understanding of cell growth and development. Houtman et al. showed that long range collective hydrodynamic interactions lead to a substantial increase in the effective velocity of motors attached to a filament. Their results were also supported by experiments.
5. Conclusion
In conclusion, hydrodynamic interactions influence substantially the dynamics of a ratchet dimer Brownian motor; consequently they have to be considered in any theory where the molecular motors are in a liquid medium.
NOTES
*On leave from Instituto de Física, Universidade Federal de Goiás, Goiânia, Brazil.