Received 8 February 2015; accepted 22 February 2015; published 26 February 2015


1. Introduction
We denote by capital letter A, B et al. the bounded linear operators on a complex Hilbert space H. An operator T on H is said to be positive, denoted by 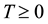 if
if  for all
for all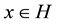 .
.
M. Ito and T. Yamazaki [1] obtained relations between two inequalities
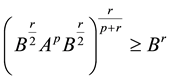 and
and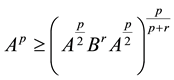 , (1.1)
, (1.1)
and Yamazaki and Yanagida [2] obtained relation between two inequalities
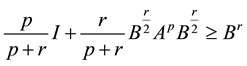 and
and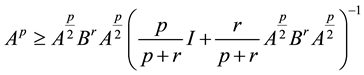 , (1.2)
, (1.2)
for (not necessarily invertible) positive operators A and B and for fixed 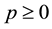 and
and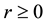 . These results led M. Ito [3] to obtain relation between two operator inequalities
. These results led M. Ito [3] to obtain relation between two operator inequalities
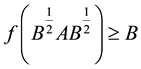 and
and![]() , (1.3)
, (1.3)
for (not necessarily invertible) positive operators A and B, where f and g are non-negative continuous functions on ![]() satisfying
satisfying![]() .
.
Remarks (1.1): The two inequalities in (1.1) are closely related to Furuta inequalities [4] .
The inequalities in (1.1) and (1.2) are equivalent, respectively, if A and B are invertibles; but they are not always equivalent. Their equivalence for invertible case was shown in [5] .
Motivated by the result (1.3) of M. Ito [3] , we obtain the results taking representing functions f and g as non-negative continuous invertible functions on ![]() satisfying
satisfying![]() .
.
2. Main Results
We denote by ![]() the kernel of an operator T.
the kernel of an operator T.
Theorem 1: Let A and B be positive invertible operators, and let f and g be non-negative invertible continuous functions on ![]() satisfying
satisfying![]() . Then the following hold:
. Then the following hold:
1) ![]() ensures
ensures ![]()
2) ![]() ensures
ensures![]() .
.
Here ![]() and
and ![]() denote orthoprojections to
denote orthoprojections to ![]() and
and ![]() respectively.
respectively.
The following Lemma is helpful in proving our results:
Lemma 2: If ![]() is a continuous function on
is a continuous function on ![]() and T is an invertible operator with
and T is an invertible operator with![]() , then
, then
![]() .
.
Proof of Lemma: Since ![]() is a continuous function on
is a continuous function on![]() , it can be uniformly approximated by a
, it can be uniformly approximated by a
sequence of polynomials on![]() . We may assume that
. We may assume that ![]() itself is a polynomial
itself is a polynomial![]() . Then
. Then
![]()
Hence the result.
Proof of Theorem 1: For![]() , let
, let ![]() and
and![]() ;
; ![]()
1) We suppose that![]() . Then
. Then
![]()
Let ![]() and
and ![]() then
then
![]()
We have![]() .
.
Further since ![]() increases as
increases as ![]() decreases and
decreases and
![]()
we have
![]() .
.
Then
![]()
i.e.
![]()
2) We suppose that![]() ; i.e.
; i.e.![]() , then
, then
![]() .
.
With ![]() and
and![]() , we have by Lemma 2
, we have by Lemma 2
![]()
Now as ![]() and since
and since
![]()
we have
![]() .
.
Then
![]()
thus completing the proof of 2.
Corollary 3. Let A and B be positive invertible operators, and let f and g be non-negative continuous invertible functions on ![]() satisfying
satisfying![]() .
.
1) If ![]() or
or![]() , then
, then ![]() ensures
ensures![]() .
.
2) If![]() , then
, then ![]() ensures
ensures![]() .
.
Proof 1) This result follows from 1) of Theorem 1 because each of the conditions ![]() and
and
![]() implies
implies![]() , so that
, so that
![]()
2) This result follows from 2) of Theorem (1) because![]() , so that
, so that
![]()
Hence the proof is complete.
Remark (3.1) 1) If![]() , then automatically
, then automatically ![]() since
since![]() , so 1) of corollary 3 holds without any conditions.
, so 1) of corollary 3 holds without any conditions.
2) The invertibility of positive operators A and B is necessary condition.
3) We have considered ![]() instead of
instead of ![]() because the requirement of the limit.
because the requirement of the limit.
![]() when
when ![]() is not fulfilled, rather it is fulfilled when
is not fulfilled, rather it is fulfilled when ![]() because
because![]() .
.
We have the following results as a consequence of corollary 3.
Theorem 4: Let A and B be positive invertible operators. Then for each ![]() and
and![]() , the following hold
, the following hold
1) If ![]() then
then![]() .
.
2) If ![]() and
and ![]() then
then![]() .
.
In Theorem 4 we consider that ![]() for
for ![]() or
or ![]() when
when ![]() and we define
and we define ![]() for a positive invertible operator T.
for a positive invertible operator T.
Theorem 5: Let A and B be positive invertible operators. Then for each ![]() and
and![]() , the following hold:
, the following hold:
1) If![]() , then
, then![]() .
.
2) If ![]() and
and![]() , then
, then ![]() .
.
Proof of Theorem 4: 1) First we consider the case when ![]() and
and![]() .Replacing A with Ap and B with
.Replacing A with Ap and B with
![]() and putting
and putting ![]() and
and ![]() in 1) of Corollary 3 so that
in 1) of Corollary 3 so that![]() , we have
, we have
if ![]() then
then![]() . (5.1)
. (5.1)
If ![]() and
and ![]() (5.1) means that
(5.1) means that
if ![]() then
then ![]()
i.e., if ![]() then
then ![]()
i.e., if ![]() then
then ![]()
i.e., if ![]() then
then ![]()
or in other words, ![]() ensures
ensures![]() .
.
But, since ![]() implies
implies![]() , it follows an equivalent assertion
, it follows an equivalent assertion ![]() ensures
ensures![]() , i.e.,
, i.e., ![]() which is further equivalent to the trivial assertion
which is further equivalent to the trivial assertion ![]() ensures
ensures![]() .
.
2) Again first we consider the case ![]() and
and![]() . Replacing A with
. Replacing A with ![]() and B with Ap and putting
and B with Ap and putting
![]() and
and ![]() in 2) of Corollary 3.
in 2) of Corollary 3.
Since![]() , we have
, we have
![]() ensures
ensures![]() . (5.2)
. (5.2)
If p = 0 and r > 0, (5.2) means that ![]() ensures
ensures ![]() i.e.,
i.e., ![]()
ensures![]() , (5.3)
, (5.3)
which implies that![]() .
.
Hence (5.3) means that ![]() ensures
ensures![]() , i.e.
, i.e. ![]() ensures
ensures![]() .
.
Hence the result.
Proof of Theorem 5: We can prove by the similar way to Theorem 4 for ![]() and
and![]() , replacing A with Ap and B with
, replacing A with Ap and B with ![]() and putting
and putting ![]() and
and ![]() for 1) in 1) of Corollary 3 and replacing A with
for 1) in 1) of Corollary 3 and replacing A with ![]() and B with Ap and putting
and B with Ap and putting ![]() and
and ![]() for 2) in 2) of Corollary 3.
for 2) in 2) of Corollary 3.
Corollary 4: Let A and B be positive invertible operators, and let f and g be non-negative continuous invertible functions on ![]() satisfying
satisfying![]() . If
. If![]() , then
, then
![]() .
.
Proof: The proof ![]() follows directly by applying the condition
follows directly by applying the condition![]() , in 1) of Corollary 3 and for the proof
, in 1) of Corollary 3 and for the proof ![]() we have only to interchange the roles of A and B and those of f and g in 2) of Corollary 3, Since
we have only to interchange the roles of A and B and those of f and g in 2) of Corollary 3, Since ![]() if
if![]() .
.