Generalized Spectrum of Steklov-Robin Type Problem for Elliptic Systems ()
1. Introduction
We study the generalized Steklov-Robin eigenproblem. This spectrum includes the Steklov, Neumann and Robin spectra. We therefore generalize the results in [1] -[4] .
Consider the elliptic system
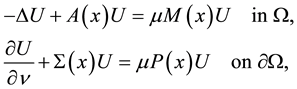 (1)
(1)
where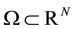 ,
,  is a bounded domain with boundary
is a bounded domain with boundary 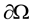 of class
of class ,
,
 Throughout this paper all matrices are symmetric. The matrix
Throughout this paper all matrices are symmetric. The matrix

verifies the following conditions:
(A1) The functions 
(A2)  is positive semidefinite a.e. on Ω with
is positive semidefinite a.e. on Ω with  for
for  when
when , and
, and  when
when 
The matrix

satisfies the following conditions:
(M1)  is positive semidefinite a.e. on Ω The functions
is positive semidefinite a.e. on Ω The functions ![]() for
for ![]() when
when![]() , and
, and ![]() when
when ![]()
![]() is the outward (unit) normal derivative on
is the outward (unit) normal derivative on ![]() The matrix
The matrix
![]()
verifies the following conditions:
(S1) The functions ![]()
(S2) ![]() is positive semidefinite a.e. on
is positive semidefinite a.e. on ![]() with
with ![]() for
for ![]() when
when![]() , and
, and ![]() when
when ![]()
and the matrix
![]()
(P1) ![]() is positive semidefinite a.e. on
is positive semidefinite a.e. on ![]() for
for ![]() when
when![]() , and
, and ![]() when
when ![]()
We assume that ![]() verify the following assumptions:
verify the following assumptions:
Assumption 1. 1) ![]() is positive definite on a set of positive measure of Ω,
is positive definite on a set of positive measure of Ω,
2) ![]() is positive definite on a set of positive measure of
is positive definite on a set of positive measure of ![]()
3) ![]() is positive definite on a set of positive measure of Ω with
is positive definite on a set of positive measure of Ω with ![]()
4) ![]() is positive definite on a set of positive measure of
is positive definite on a set of positive measure of ![]()
Remark 2. Assumption 1 is equivalent to
![]()
Remark 3. Since ![]() satisfy (A2), (S2), (M1), (P1) respectively, then we can write them in the following form (i.e.; eigen-decomposition of a positive semi-definite matrix or diagonalization)
satisfy (A2), (S2), (M1), (P1) respectively, then we can write them in the following form (i.e.; eigen-decomposition of a positive semi-definite matrix or diagonalization)
![]()
where ![]() (
(![]() i.e.; are orthogonal matrices) are the normalized eigenvectors, I is the identity matrix,
i.e.; are orthogonal matrices) are the normalized eigenvectors, I is the identity matrix, ![]() is diagonal matrix and in the diagonal of
is diagonal matrix and in the diagonal of ![]() are the eigenvalues of J (i.e.;
are the eigenvalues of J (i.e.;![]() ) and
) and ![]()
Remark 4. The weight matrices ![]() and
and ![]() may vanish on subsets of positive measure.
may vanish on subsets of positive measure.
Definition 1. The generalized Steklov-Robin eigensystem is to find a pair ![]() with
with ![]() such that
such that
![]() (2)
(2)
Remark 5. Let ![]() in (2) if there is such an eigenpair, then
in (2) if there is such an eigenpair, then ![]() and
and
![]()
Indeed, if ![]() or
or ![]() then
then
![]()
We have that ![]() which implies that
which implies that ![]() and
and ![]() this implies that
this implies that
![]() a.e. (with
a.e. (with![]() ) in Ω. This implies that
) in Ω. This implies that ![]() is not positive definite on a subset of Ω of
is not positive definite on a subset of Ω of
positive measure, and ![]() then
then ![]() a.e. with
a.e. with ![]() on
on ![]() This implies
This implies
that ![]() is not positive definite on subset of
is not positive definite on subset of ![]() of positive measure. So we have that,
of positive measure. So we have that, ![]() would be a constant vector function; which would contradict the assumptions (Assumption 1) imposed on
would be a constant vector function; which would contradict the assumptions (Assumption 1) imposed on ![]() and
and ![]()
Remark 6. If ![]() and
and ![]() then
then ![]() is an eigenvalue of the system (1) with eigenfunction
is an eigenvalue of the system (1) with eigenfunction ![]() vector function on
vector function on![]() .
.
It is therefore appropriate to consider the closed linear subspace (to be shown below) of ![]() under Assumption 1 defined by
under Assumption 1 defined by
![]()
Now all the eigenfunctions associated with (2) must belong to the ![]() -orthogonal complement
-orthogonal complement
![]() of this subspace in
of this subspace in ![]() We will show that indeed
We will show that indeed ![]() is subspace of
is subspace of
![]() Let
Let ![]() and
and ![]() we wish to show that
we wish to show that ![]() and
and ![]()
![]()
Therefore ![]() Now we show that
Now we show that ![]()
![]()
Since ![]() it follows that
it follows that
![]()
By setting ![]() we get
we get
![]()
Since ![]() for a.e.
for a.e. ![]() it readily follows that
it readily follows that
![]()
that is, the vector ![]() satisfies
satisfies
![]()
or equivalently
![]()
Hence,
![]()
since ![]() A similar arguments shows that
A similar arguments shows that
![]()
Therefore ![]() so we have that
so we have that ![]() is a subspace of
is a subspace of ![]() Thus, one can split the Hilbert space
Thus, one can split the Hilbert space ![]() as a direct
as a direct ![]() -orthogonal sum in the following way
-orthogonal sum in the following way
![]()
Remark 7. 1) If ![]() in Ω, then the subspace
in Ω, then the subspace ![]() provided
provided ![]() on
on![]() .
.
2) If ![]() in
in ![]() and
and![]() , then the subspace
, then the subspace ![]() provided
provided ![]() on Ω.
on Ω.
・ We shall make use in what follows the real Lebesgue space ![]() for
for![]() , and of the continuity and compactness of the trace operator
, and of the continuity and compactness of the trace operator
![]()
is well-defined, it is a Lebesgue integrable function with respect to Hausdorff ![]() dimensional measure. Sometimes we will just use U in place of
dimensional measure. Sometimes we will just use U in place of ![]() when considering the trace of a function on
when considering the trace of a function on![]() . Throughout, this work we denote the
. Throughout, this work we denote the ![]() -inner product by
-inner product by
![]()
and the associated norm by
![]()
(see [5] , [6] and the references therein for more details).
・ The trace mapping ![]() is compact (see [7] ).
is compact (see [7] ).
![]() (3)
(3)
defines an inner product for![]() , with associated norm
, with associated norm
![]() (4)
(4)
Now, we state some auxiliary result, which will be need in the sequel for the proof of our main result. Using the Hölder inequality, the continuity of the trace operator, the Sobolev embedding theorem and lower semicontinuity of![]() , we deduce that
, we deduce that ![]() is equivalent to the standard
is equivalent to the standard ![]() -norm. This observation enables us to prove the existence of an unbounded and discrete spectrum for the Steklov-Robin eigenproblem (1) and discuss some of its properties.
-norm. This observation enables us to prove the existence of an unbounded and discrete spectrum for the Steklov-Robin eigenproblem (1) and discuss some of its properties.
Definition 2. Define the functional
![]()
![]()
and
![]()
![]()
Lemma 1. Suppose (A2), (S2), (M1), (P1) are met. Then the functionals ![]() and
and ![]() are C1-functional (i.e.; continuously differentiable).
are C1-functional (i.e.; continuously differentiable).
See [8] for the proof of Lemma 1.
Theorem 8. ![]() is G-differentiable and convex. Then
is G-differentiable and convex. Then ![]() is weakly lower-semi-continuous.
is weakly lower-semi-continuous.
See [8] for the proof of Theorem 8.
2. Main Result
Theorem 9. Assume Assumption 1 as above, then we have the following.
1) The eigensystem (1) has a sequence of real eigenvalues
![]()
and each eigenvalue has a finite-dimensional eigenspace.
2) The eigenfunctions ![]() corresponding to the eigenvalues
corresponding to the eigenvalues ![]() from an
from an ![]() -orthogonal and
-orthogonal and ![]() - orthonormal family in
- orthonormal family in ![]() (a closed subspace of
(a closed subspace of![]() ).
).
3) The normalized eigenfunctions provide a complete ![]() -orthonormal basis of
-orthonormal basis of ![]() Moreover, each function
Moreover, each function ![]() has a unique representation of the from
has a unique representation of the from
![]() (5)
(5)
In addition,
![]()
Proof of Theorem 9. We will prove the existence of a sequence of real eigenvalues ![]() and the eigenfunc-
and the eigenfunc-
tions ![]() corresponding to the eigenvalues that from an orthogonal family in
corresponding to the eigenvalues that from an orthogonal family in![]() .
.
We show that ![]() attains its minimum on the constraint set
attains its minimum on the constraint set
![]()
Let ![]() by using the continuity of the trace operator, the Sobolev embedding theorem and
by using the continuity of the trace operator, the Sobolev embedding theorem and
the lower-semi-continuity of ![]()
Let ![]() be a minimizing sequence in W0 for
be a minimizing sequence in W0 for ![]() since
since ![]() we have that
we have that ![]() by the definition of
by the definition of ![]() we have that for all
we have that for all ![]() and for all sufficiently large l, then
and for all sufficiently large l, then ![]() by using the equivalent norm we have that, there is exist
by using the equivalent norm we have that, there is exist ![]() such that
such that
![]()
so we have that
![]()
Therefore, this sequence is bounded in![]() . Thus it has a weakly convergent subsequence
. Thus it has a weakly convergent subsequence ![]()
which convergent weakly to ![]() in
in![]() . From Rellich-Kondrachov theorem this subsequence converges strongly to
. From Rellich-Kondrachov theorem this subsequence converges strongly to ![]() in
in ![]() so
so ![]() in W0. Thus
in W0. Thus ![]() as the functional is weakly l.s.c. (see Theorem 8).
as the functional is weakly l.s.c. (see Theorem 8).
There exists ![]() such that
such that![]() . Hence,
. Hence, ![]() attains its minimum at
attains its minimum at ![]() and
and ![]() satisfies the following
satisfies the following
![]() (6)
(6)
for all ![]() We see that
We see that ![]() satisfies Equation (2) in a weak sense and
satisfies Equation (2) in a weak sense and ![]() this im-
this im-
plies that ![]() by the definition of W0. Now take
by the definition of W0. Now take ![]() in Equation (6), we obtain that the eigenvalue
in Equation (6), we obtain that the eigenvalue ![]() is the infimum
is the infimum![]() . This means that we could define
. This means that we could define ![]() by the Rayleigh quotient
by the Rayleigh quotient
![]()
Clearly,![]() . Indeed assume that
. Indeed assume that ![]() then
then ![]() on
on ![]() hence
hence ![]() must be a constant and
must be a constant and ![]() with
with ![]() that contradicts the assumptions imposed on
that contradicts the assumptions imposed on![]() . Thus
. Thus![]() .
.
Now we show the existence of higher eigenvalues.
Define
![]()
We know that the kernel of ![]()
![]()
Since W1 is the null-space of the continuous functional ![]() on
on ![]() W1 is a closed sub-
W1 is a closed sub-
space of![]() , and it is therefore a Hilbert space itself under the same inner product
, and it is therefore a Hilbert space itself under the same inner product![]() . Now
. Now
we define
![]()
Since ![]() then we have that
then we have that![]() . Now we define
. Now we define
![]()
we know that the kernel of ![]()
![]()
Since W2 is the null-space of the continuous functional ![]() on
on![]() , W2 is a closed subspace of
, W2 is a closed subspace of![]() , and it is therefore a Hilbert space itself under the same inner product
, and it is therefore a Hilbert space itself under the same inner product![]() . Now
. Now
we define
![]()
Since ![]() then we have that
then we have that ![]() Moreover, we can repeat the above arguments to show that
Moreover, we can repeat the above arguments to show that ![]()
is achieved at some ![]()
We let
![]()
and
![]()
Since ![]() then we have that
then we have that![]() . Moreover, we can repeat the above arguments to show that
. Moreover, we can repeat the above arguments to show that ![]()
is achieved at some ![]()
Proceeding inductively, in general we can define
![]()
we know that the kernel of ![]()
![]()
Since Wj is the null-space of the continuous functional ![]() on
on![]() , Wj is a closed subspace
, Wj is a closed subspace
of![]() , and it is therefore a Hilbert space itself under the same inner product
, and it is therefore a Hilbert space itself under the same inner product ![]() Now we define
Now we define
![]()
In this way, we generate a sequence of eigenvalues
![]()
whose associated ![]() are c-orthogonal and
are c-orthogonal and ![]() -orthonormal in
-orthonormal in ![]()
Claim 1 ![]() as
as ![]()
Proof of claim 1. By way of contradiction, assume that the sequence is bounded above by a constant. Therefore, the corresponding sequence of eigenfunctions ![]() is bounded in
is bounded in ![]() By Rellich-Kondrachov theorem and the compactness of the trace operator, there is a Cauchy subsequence (which we again denote by
By Rellich-Kondrachov theorem and the compactness of the trace operator, there is a Cauchy subsequence (which we again denote by![]() ), such that
), such that
![]() (7)
(7)
Since the ![]() are
are ![]() -orthonormal, we have that
-orthonormal, we have that![]() , if
, if ![]()
which contradicts Equation (7). Thus, ![]() We have that each
We have that each ![]() occurs only finitely many times.
occurs only finitely many times.
Claim 2
Each eigenvalue ![]() has a finite-dimensional eigenspace.
has a finite-dimensional eigenspace.
See [8] for the proof of claim 2.
We will now show that the normalized eigenfunctions provide a complete orthonormal basis of![]() . Let
. Let
![]()
so that ![]()
Claim 3
The sequence ![]() is a maximal
is a maximal ![]() -orthonormal family of
-orthonormal family of![]() . (We know that the set is
. (We know that the set is
maximal ![]() -orthonormal if and only if it is a complete orthonormal basis).
-orthonormal if and only if it is a complete orthonormal basis).
Proof of Claim 3. By way of contradiction, assume that the sequence ![]() is not maximal, then there exists a
is not maximal, then there exists a ![]() and
and ![]() such that
such that ![]() and
and![]() , i.e.;
, i.e.;
![]()
since![]() . Therefore
. Therefore![]() . We have that
. We have that![]() . It follows from the definition of
. It follows from the definition of ![]() that
that
![]()
Since we know from Claim 1 that ![]() as
as ![]() we have that
we have that ![]() Therefore
Therefore ![]() a.e in Ω, which contradicts the definition of ξ. Thus the sequence
a.e in Ω, which contradicts the definition of ξ. Thus the sequence ![]() is a maximal
is a maximal ![]() -orthonormal family of
-orthonormal family of ![]() so the sequence
so the sequence ![]() provides a complete orthonormal basis of
provides a complete orthonormal basis of ![]() that is, for any
that is, for any![]() ,
, ![]() with
with ![]() and
and
![]()
![]()
Now let
![]()
Therefore,
![]()
and
![]()
Claim 4
We shall show that
![]()
Proof of Claim 4.
![]()
Thus
![]()