An Efficient and Robust Fall Detection System Using Wireless Gait Analysis Sensor with Artificial Neural Network (ANN) and Support Vector Machine (SVM) Algorithms ()
1. Introduction
It is estimated that one third of the senior citizens in the United States (i.e., around 12 million people) fall each year, which often results in serious injuries [1] . Falls in elderly persons living alone can be especially dangerous. Therefore, it is important to introduce a highly accurate and easy-to-wear fall detection device that can wirelessly detect and record real-time falls for the aging population. We have performed investigation using our custom sensor without the wireless feature and achieved 100% accuracy in identifying all 60 falls vs. the Activities of Daily Living (ADL) with no false positives on young volunteers using threshold based algorithms [2] . For this current work, the sensor is wireless and allows for real-time untethered testing for not only fall detections, but also for gait analysis [2] [3] . This paper reports our new Wireless Gait Analysis Sensor (WGAS) used specifically for real-time automatic fall detection with an efficient Back Propagation Artificial Neural Network (BP ANN) algorithm with different training schemes and Support Vector Machine (SVM) with different kernel functions. This WGAS is placed and tested at two different positions on the body: at the T4 position and at the Belt position using a belt clip as shown in Figure 1.
For the learning of BP ANN and SVM, the following 6 features (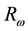 : Range of angular velocity;
: Range of angular velocity;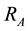 : Range of acceleration) as shown in Equations (1) and (2) were extracted from the raw data taken from WGAS. They are used to perform real-time fall detection as supplied as inputs to these classifiers.
: Range of acceleration) as shown in Equations (1) and (2) were extracted from the raw data taken from WGAS. They are used to perform real-time fall detection as supplied as inputs to these classifiers.
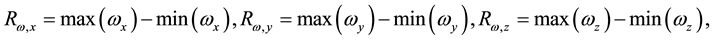 (1)
(1)
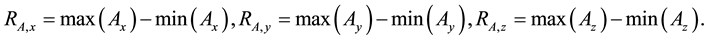 (2)
(2)
2. Wireless Gait Analysis Sensor
The custom-designed WGAS consists of a 3-axis linear accelerometer, a single axis gyroscope, and a dual axis gyroscope to measure 3-D human body translations and rotations during a gait pattern with the help of the Micro- Electrical and Mechanical System (MEMS) sensors integrated on a PCB. This WGAS system is supported by a Texas Instruments (TI) MSP430 microcontroller, and a wireless 2.4 GHz USB transceiver using the SimpliciTI™ protocol with a range of ~12 meters (40 ft). An overall simplified system block diagram for the WGAS fall detection system is shown in Figure 2. The 2 AAA batteries used in our earlier wired sensor [2] were replaced by
![]()
![]()
![]()
Figure 1. Sensor orientation and location at the belt position on a belt clip (left) and at T4 (right).
![]()
Figure 2. A simplified block diagram of the WGAS fall detection system.
a single rechargeable Li-ion coin battery, providing a battery lifetime of ~40 hours continuous operation time with each recharge. The PCB, coin battery and the microcontroller are placed in a specially designed 3D printed box 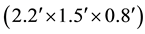 with a total weight of 42 grams. The design of the box was done with a 3D modeling software Rhinoceros (Rhino) and printed using a 3D printer with Acrylonitrile Butadiene Styrene (ABS) plastic. The box has a sliding lid and shown in Figure 3.
with a total weight of 42 grams. The design of the box was done with a 3D modeling software Rhinoceros (Rhino) and printed using a 3D printer with Acrylonitrile Butadiene Styrene (ABS) plastic. The box has a sliding lid and shown in Figure 3.
The accelerometer data is sampled at 160 Hz and digitized to 8 bits, with its output scaled to ±6 g at 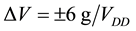
 for each axis. The gyroscope data is also sampled at 160 Hz and digitized to 8 bits, with its output scaled to 300˚ per sec. (dps) at
for each axis. The gyroscope data is also sampled at 160 Hz and digitized to 8 bits, with its output scaled to 300˚ per sec. (dps) at 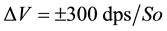 (Note the typical
(Note the typical 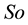 (sensitivity) value is 3.752 mV/dps for the accelerometer and 3.33 mV/dps for the gyroscopes). The sensor orientation and positions on the body are shown in Figure 1. The sensor is carefully secured to the subjects during testing to avoid artifacts. The microcontroller and the transceiver unit enables the real-time transmission of the 6-dimen- sional gait data wirelessly to the nearby PC, where a LABVIEW™ program is used for designing the Graphical User Interface (GUI) (Figure 4).
(sensitivity) value is 3.752 mV/dps for the accelerometer and 3.33 mV/dps for the gyroscopes). The sensor orientation and positions on the body are shown in Figure 1. The sensor is carefully secured to the subjects during testing to avoid artifacts. The microcontroller and the transceiver unit enables the real-time transmission of the 6-dimen- sional gait data wirelessly to the nearby PC, where a LABVIEW™ program is used for designing the Graphical User Interface (GUI) (Figure 4).
Testing Protocol
First falls [4] were performed on a cushion mattress bed by two young volunteers wearing the WGAS at T4 and on the belt (see Table 1 with 10 types of falls). The total number of falls was 101 (51 at T4 and 50 at belt). For the ADL tests [4] , same volunteers performed every ADL recorded in Table 2 (note this includes picking up an object test #7), and the aggregate number of ADLs was 69 (34 at T4 and 35 at belt). For the DGI tests [5] , the same volunteers performed every DGI test in Table 3, with 152 tests taken in total (82 at T4 and 70 at belt).
3. BP ANN Algorithm
For training the feed-forward ANN classifier, back propagation was applied according to Duda et al. [6] and a 3- layer system was picked as the standard BP ANN [7] . The input layer of the network has six neurons which correspond to the six input feature values. There is one hidden layer holding 10 hidden neurons, which number was optimized by adjusting the size of hidden neurons (from one to 15) as shown in Figure 5, where two output neurons corresponding to the two target classes the network needs to differentiate (i.e., the features of all falls are considered as Class 1, and all DGI and ADL are as Class 2). The essential idea of the back propagation learning algorithm [8] is the repeated application of the chain rule to calculate the impact of each weight in the network by taking an arbitrary error function E in to account as shown in Equation (3):
 (3)
(3)
where wij is the weight from neuron j to neuron i, si is the output, and neti is the weighted sum of the inputs of the neuron i. After calculating the derivative of each weight, the error function is minimized by following a simple gradient decent rule in Equation (4):
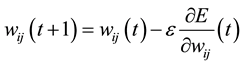 (4)
(4)
![]()
Figure 3. Physical structure of our custom-designed WGAS.
![]()
Figure 4. GUI designed in LABVIEWTM for our real-time fall detection system using the WGAS, indicating a fall occurred after 8.765 sec.
![]()
Figure 5. The 3-layer BP ANN topology used in this work.
![]()
Table 1. Intentional falls performed in this work.
![]()
Table 2. Activities of Daily Living (ADL) movements performed.
![]()
Table 3. Dynamic Gait Index (DGI) tests performed.
Clearly, the decision of the learning rate e, which scales the derivative, has a critical impact on the time required until convergence is arrived. If the learning rate is set too small, numerous steps are expected to achieve an acceptable solution. On the contrary, a large learning rate will possibly lead to oscillation, preventing the error to fall below a certain value. The training of the BP ANN is done by using three different learning algorithms dis- cussed below.
3.1. BP ANN with Scaled Conjugate Gradient (SCG) Learning
The basic back propagation algorithm alters the weights of the network following the steepest descent direction (negative direction of the slope). In this direction the performance function decreases most rapidly along the negative direction of slope. However, convergence may not be achieved even though the decrease is more rapid. Therefore, conjugate gradient methods are used which can generally produce faster convergence than gradient descent techniques by performing a search in all the gradient directions to determine the step size obtained by the learning factor. The training of the ANN classifier used in this work is done by the scaled conjugate gradient (SCG) back propagation method developed by Moller [9] . This SCG algorithm performs the search and chooses the step size by using the information from the second order error function from the neural network. The SCG training is optimized by the parameter sigma σ (which determines the change in weight for the second derivative approximation) and lamda λ (which regulates the indefiniteness of the Hessian). The values of σ and λ were taken as ![]() and
and![]() , respectively.
, respectively.
3.2. BP ANN with Levenberg-Marquardt (LM) Learning
The second training method for BP ANN is done by the Levenberg-Marquardt algorithm [10] , which is used to speed up the training of second order approximations without having to calculate the Hessian matrix. If the performance function has the sum of squares (typical in training feed-forward networks) then the Hessian matrix can be approximated as:
![]() (5)
(5)
And the gradient can be calculated as
![]() (6)
(6)
where J is the Jacobian matrix, which has the first derivatives of the network errors with respect to the weights and biases, and e is a vector that contains the network errors.
To make sure the H is always invertible, the LM algorithm introduces another approximation to the Hessian matrix using.
![]() (7)
(7)
where µ is called combination coefficient and is always positive and I is the identity matrix. The LM algorithm does the training according the scalar parameter µ. If the value of µ is zero, this algorithm reduces to the Hessian matrix approximation; and if the value of µ is large, this becomes a gradient descent algorithm with small step size. The LM training is optimized by the parameter µ (i.e., the combination coefficient). As µ can either be small or large, its value is initialized to 0.001 and the maximum value is set to![]() , with a decrease factor of 0.1 and an increase factor of 10.
, with a decrease factor of 0.1 and an increase factor of 10.
3.3. BP ANN with Resilient Propagation (RPROP)
In training the feed-forward ANN we generally use sigmoid transfer functions in the hidden layer that are characterized by the principle that its slope must reach zero as the input gets large. This can cause problems because if the gradient gets too small, there is a chance that we can only apply small changes in the weights and biases of the network, even though they are far from their global optimal values. Therefore, the reason for using the resilient back propagation (RPROP) is to eliminate these undesired effects [11] . Only the sign of the derivative can determine the weighting update; the magnitude of the derivative has no effect on updating the weights. The RPROP training is optimized by choosing ![]() (Initial weight change) to 0.07, the weight change increment to 1.2, and the weight change decrement equals to 0.5.
(Initial weight change) to 0.07, the weight change increment to 1.2, and the weight change decrement equals to 0.5.
4. Support Vector Machine (SVM)
Support Vector Machine (SVM) is a method for patterns recognition/classification on two categories with supervised learning. SVM-light, one of the implementation of SVM proposed by Thorsten Joachims [12] [13] , is applied to classification of experimental data into falls, DGI and ADL.
4.1. Linear SVM Classification
The optimization algorithm for linear classification was proposed by Vapnik [14] . This algorithm finds the maxi- mum-margin hyper-plane from given training data set D as described in Equation (8):
![]() (8)
(8)
where ![]() is either 1 or 1 and n is the number of training data. Each
is either 1 or 1 and n is the number of training data. Each ![]() is a p-dimensional vector having the fea- ture quantity
is a p-dimensional vector having the fea- ture quantity![]() . Any hyper-plane can be written as:
. Any hyper-plane can be written as:
![]() (9)
(9)
where ![]() is the vector to the hyper-plane. If the training data are linearly separable, the hyper-plane can be described as:
is the vector to the hyper-plane. If the training data are linearly separable, the hyper-plane can be described as:
![]() (10)
(10)
The distance between these two hyper-plane is![]() , so the purpose is to minimize
, so the purpose is to minimize![]() . Therefore, the algorithm can be rewritten as:
. Therefore, the algorithm can be rewritten as:
![]() (11)
(11)
We can also reformulate the equation without changing the solution as following:
![]() (12)
(12)
In Linear SVM, a hyper-plane or a set of hyper-planes can be used as the separate lines in classification. The higher the margin of separation for the classes that can be created, the better the classification result that can generally be achieved for the Linear SVM [15] .
4.2. Nonlinear SVM Classification
B. E. Boser et al. proposed the nonlinear SVM classifiers by using the kernel trick [16] . The kernel functions used in this study are as followed:
![]() (13)
(13)
![]() (14)
(14)
The accuracy of SVM depends on the kernel, cost factor parameter C [17] and the parameter ![]() for the RBF kernel. We checked each combination of parameter choices in this work, and looked up for the best accuracy.
for the RBF kernel. We checked each combination of parameter choices in this work, and looked up for the best accuracy.
4.3. Overall Data Analysis Flow-Chart
After getting the raw data from the WGAS, feature extraction is performed by extracting 6 features as shown in Equations (1)-(2) and the training algorithms are implemented to obtain the fall detection. Figure 6 shows the complete data analysis flow chart of the WGAS system.
5. Classification Results
5.1. Classification Results Using the BP ANN Algorithm
Fall detection using BP ANN is done on WGAS data taken at both T4 and at belt positions with three training schemes. The data was obtained using a 1.7 GHz PC with 4 GB of RAM, Windows 8 OS, and the MATLAB R2013b for the BP ANN classifier model. For the trained BP ANN classifier model, the number of training, validation and testing data sets were divided into 70-15-15 and 50-25-25 in percentages, respectively for all the three training schemes. The classification results of SCG, LM and RPROP training schemes are shown in the Table 4 and Table 5. From Table 4 for the data at T4, LM and RPROP obtained the best overall Correct Detection Rate (CDR) of 98.2% for the training-validation-testing (50% - 25% - 25%) data sets. And at the belt position from Table 5, LM yielded an overall CDR of 98.70% for the training-validation-testing (70% - 15% - 15%) data sets, and SCG yielded an overall CDR of 98.70% for the training-validation-testing (50% - 25% - 25%) data sets.
![]()
Figure 6. The data analysis flow-chart of the WGAS fall detection system.
![]()
Table 4. BP ANN classification results from the T4 data.
*SCG: scaled conjugate gradient; LM: levenberg-marquardt; RP: resilient propagation.
![]()
Table 5. BP ANN classification results from the belt position data.
*SCG: scaled conjugate gradient; LM: levenberg-marquardt; RP: resilient propagation.
The performance indicators such as specificity and sensitivity were also calculated by using Equations (14)- (15) and shown in Table 4 and Table 5.
![]() (15)
(15)
![]() (16)
(16)
where TN (true negatives) are the ADLs and DGIs correctly classified, FP (false positives) are the ADLs and DGIs that were not correctly classified by the BP ANN/SVM; TP (true positives) are the falls correctly classified and FN (false negatives) are the falls that were not detected by the BP ANN/SVM.
5.2. Classification Results Using the SVM Algorithm
Fall detection using SVM is done on WGAS data taken at both T4 and at the belt position with three kernels. The data was obtained using a 1.7 GHz PC with 2 GB of RAM, Ubuntu 9.04 OS for running the SVM-light v6.01. For the trained SVM classifier, the number of training, validation and testing data sets were divided into 70-15-15, 50-25-25 in percentage, respectively for all the three kernels. The SVM classification results and the final parameters are shown in Table 6 and Table 7. Correct Detection Rate (CDR) of 98.8% have been achieved by taking data at the T4 for training-validation-testing (70% - 15% - 15%) data sets using the RBF kernel from
![]()
Table 6. SVM classification results from the T4 data.
*RBF: radial basis function.
![]()
Table 7. SVM classification results from the belt position data.
*RBF: radial basis function.
Table 6. From Table 7, we achieved 98.71% CDR at the belt position for training-validation-testing (70% - 15% - 15%) data sets by the RBF kernel.
6. Conclusions
Our custom Wireless Gait Analysis Sensor (WGAS) was applied for real-time automatic fall detection with a simple but very fast BP ANN using 6 input features trained by the Back Propagation Artificial Neural Network (BP ANN), and also with a Support Vector Machine (SVM) classifier. From Tables 4-7, LM and RPROP train- ed BP ANN has the highest specificity of 97.4%, and the highest sensitivity of 100% at the T4 position. SCG trained BP ANN achieves the highest specificity of 100%, and LM trained BP ANN has the highest sensitivity of 100% at the Belt position. Similarly, the RBF kernel SVM reaches the highest specificity of 100%, and the highest sensitivity of 94.1% at the T4 position. The Linear kernel SVM has the highest specificity of 100%, and the Polynomial kernel SVM has the highest sensitivity of 100%. Overall, the SVM shows a slightly lower sensitivity than the BP ANN. This is likely because the SVM uses an RBF kernel as the activation function, whereas the BP ANN uses a tan sigmoid (Tanh) function that has better recognition accuracy.
The preliminary data that was collected on the group of young volunteers reported here suggests that our real- time fall detection system performs competitively regardless if the WGAS is placed at the T4 or waist-level Belt position. The application of the WGAS is not only useful for the fall detection, but also for the gait analysis. However, to make our fall detection work to be clinically relevant, a bit more data should be collected during clinical trials at TTUHSC in order to carefully evaluate the performance of the classifiers and their classification accuracies using the WGAS on patients. Our WGAS has passed the TTUHSC IRB (Internal Review Board), and is going through clinical trials on patients with balance disorders. The initial results look rather promising for gaits differentiation.