Explanation of Capacitive Performance of the Plasma in Damavand Tokamak ()
1. Introduction
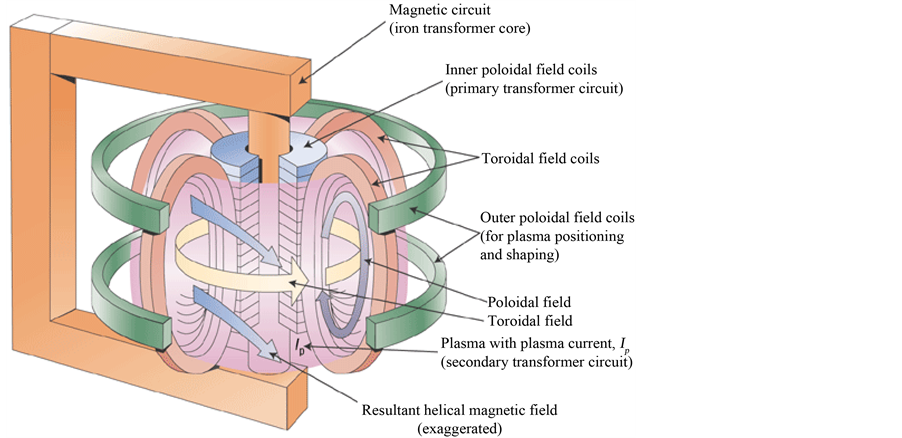
Tokamak is a torodial shape magnetic confinement fusion device that is the best candidate for nuclear fusion reactors [1] [2] . Working principle of this device is like a transformer, passing the electric current through the primary coils inducing a current in the tokamak plasma that plays the role of secondary coils of transformer (Figure 1) [1] -[3] . This current causes heating of the plasma and creates a polar magnetic field Bθ which increases the quality of the confinement of tokamak plasmas. The resistive and inductive properties of the plasma in tokamak have been widely studied. Though the plasma has capacitance property in all area between its centre and the chamber wall, its capacitive performance was not widely studied before 1990’s [4] [5] . In this article, the capacitive property of the plasma in the tokamak and its importance in circuit equations and transport codes of tokamak is explained. Then, the numerical results of such model for Damavand tokamak compare with experimental results and a good agreement between them is observed.
2. The Capacitive Model
Estimation the value of capacitance of the equal circuit of tokamak can be done by a torodial coaxial capacitor (Figure 2), the tokamak plasma plays the role of inner electrode and the discharge chamber wall is external electrode and the low-density plasma between them considered as the dielectric of capacitor. In this article, the capacity of tokamak plasma obtained through solving the Laplace equation for a torus, and the working regimes in which this property is important have been identified.
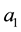 ,
, 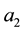 and
and 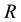 are the distance between centre of plasma and its edge, tokamak minor radius and major radius of the tokamak, respectively. Here the main problem is the solving of the Laplace equation for
are the distance between centre of plasma and its edge, tokamak minor radius and major radius of the tokamak, respectively. Here the main problem is the solving of the Laplace equation for 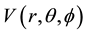 with the boundary conditions of (
with the boundary conditions of ( in
in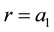 ) and (
) and (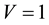 in
in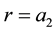 ).
).
The Laplace equation [6] :
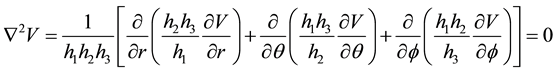 (1)
(1)
 ,
,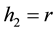 and
and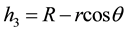
With substituting the above values in Equation (1) and with respect to that in this system 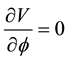 the Equa-
the Equa-
tion (1) becomes as follows.
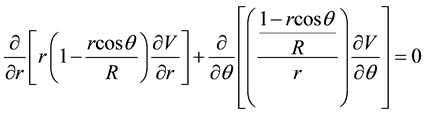 (2)
(2)
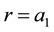 :
: 
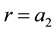 :
: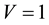
Because of the uniqueness of the solutions of Laplace equation, there will be only one answer that will satisfy the above conditions.
It is obvious that in a constant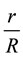 , the solution of Equation (2)
, the solution of Equation (2) ![]() will be a periodic function of
will be a periodic function of ![]() that its
that its
period is![]() . It is also evident that because of symmetry
. It is also evident that because of symmetry ![]() is a paired function of
is a paired function of![]() . Thus,
. Thus, ![]() can be de-
can be de-
scribed as a cosine Fourier series of ![]() as the following form in which coefficients
as the following form in which coefficients ![]() are functions of
are functions of![]() :
:
![]() (3)
(3)
Now, it is necessary to obtain expressions for ![]() that can satisfy the boundary conditions, for finding
that can satisfy the boundary conditions, for finding
the simplest solution, we first put the ![]() from Equation (3) instead of
from Equation (3) instead of ![]() in Equation (2) and equals
in Equation (2) and equals
the coefficients of ![]() in the resulting equation to zero for any natural number of
in the resulting equation to zero for any natural number of ![]() more than 1. Finally, the following expressions obtain for
more than 1. Finally, the following expressions obtain for ![]() and
and![]() :
:
![]() (4)
(4)
![]()
On the other hand, the solution to Laplace equation for such coordinate system would be in the form of
![]()
This solution provides the boundary conditions ![]() and
and ![]() and is completely independent from
and is completely independent from![]() . We can calculate the capacity of capacitor in Figure 2 if the charge on each torus can be measured.
. We can calculate the capacity of capacitor in Figure 2 if the charge on each torus can be measured.
With respect to that the boundaries are considered as co-potential surface, on them![]() . Therefore, the
. Therefore, the
electrical charge on each surface of torus is equal to ![]() in which the integral is done over the entire of surface.
in which the integral is done over the entire of surface.
In this relation ![]() and
and ![]() is the coefficient of permittivity of dielectric material and
is the coefficient of permittivity of dielectric material and
![]() .
.
![]() (5)
(5)
By putting the calculated values for ![]() and
and ![]() (Equation (4)) in Equation (5)) and notice that all of the coefficients
(Equation (4)) in Equation (5)) and notice that all of the coefficients ![]() for
for ![]() are equal to zero and integrating it the value of
are equal to zero and integrating it the value of ![]() is obtained by Equation (6):
is obtained by Equation (6):
![]() (6)
(6)
Since ![]() and
and![]() , the value of capacitance can be calculated by following equation:
, the value of capacitance can be calculated by following equation:
![]() (7)
(7)
In limit of ![]() and taking into account
and taking into account ![]() Equation (7) is changed to
Equation (7) is changed to ![]() which is
which is
the same formula for capacitance in concentric cylinders. It should be noted that ![]() is the permittivity of the space between the boundary of plasma and the vacuum chamber that is a low-density plasma and can be written
is the permittivity of the space between the boundary of plasma and the vacuum chamber that is a low-density plasma and can be written
as ![]() that
that![]() ,
, ![]() is the Alfven velocity and
is the Alfven velocity and![]() ,
, ![]() and
and ![]() are the strength of
are the strength of
magnetic field, mass density and velocity of light, respectively. Because the values of ![]() in different regions are not equal, also the values of
in different regions are not equal, also the values of ![]() are different in these regions [7] . The value of
are different in these regions [7] . The value of ![]() is maximum in the centre of plasma and minimum in the space between the edge of plasma and the chamber wall, and these spaces can be considered as series capacitors.
is maximum in the centre of plasma and minimum in the space between the edge of plasma and the chamber wall, and these spaces can be considered as series capacitors.
The electrical equivalent circuit for tokamak after taking into account the capacitor property is shown in Figure 3 in which ![]() is the loop voltage,
is the loop voltage, ![]() and
and ![]() are the resistance and inductance of the plasma which are
are the resistance and inductance of the plasma which are
calculated by ![]() and
and ![]() relations, respectively. In these two
relations, respectively. In these two
equations, ![]() ,
, ![]() and
and ![]() are the effective charge of tokamak plasma, the electron temperature and the vacuum permeability coefficient, respectively [8] [9] . The equivalent circuit that has involved these capacitors consists of several meshes and its analytical solution is extremely difficult, but the results of a circuit with
are the effective charge of tokamak plasma, the electron temperature and the vacuum permeability coefficient, respectively [8] [9] . The equivalent circuit that has involved these capacitors consists of several meshes and its analytical solution is extremely difficult, but the results of a circuit with ![]() (Figure 3) are good enough for simulation the tokamak plasma. The circuit equation for Figure 3 is a second order differential equation in following form:
(Figure 3) are good enough for simulation the tokamak plasma. The circuit equation for Figure 3 is a second order differential equation in following form:
![]() (8)
(8)
In Equation (8), ![]() is obtained using Norton equivalent circuit of Figure 3 in the following way:
is obtained using Norton equivalent circuit of Figure 3 in the following way:
![]() (9)
(9)
The general solution of Equation (9) for the plasma current can be written as:
![]() (10)
(10)
![]()
Figure 3. RLC equivalent circuit of tokamak plasmas.
In Equation (10) ![]() and
and ![]() are the natural frequency (resonance) and the
are the natural frequency (resonance) and the
damping constant, respectively.![]() ,
, ![]() are the initial values of the plasma loop voltage and the plasma cur-
are the initial values of the plasma loop voltage and the plasma cur-
rent, respectively. ![]() is calculated through
is calculated through![]() . Natural frequency
. Natural frequency ![]() is an
is an
important factor that can play an important role in various regimes of the tokamak plasma. The values of natural frequencies for different tokamaks are in order of![]() .
.
In fact, according to the properties of electrical elements, in dc regimes (following the end of transient regimes), ![]() would act such as an open circuit and
would act such as an open circuit and ![]() such as a short cuircuit. Therefore, the circuit in Figure 3 is changed to a simple resistive circuit in which
such as a short cuircuit. Therefore, the circuit in Figure 3 is changed to a simple resistive circuit in which![]() . When
. When ![]() varies with time, not only the resistance circuit but also the RL model cannot correctly simulate the behaviour of the plasma. Hence, RLC model should be used.
varies with time, not only the resistance circuit but also the RL model cannot correctly simulate the behaviour of the plasma. Hence, RLC model should be used.
The first effects of capacitance are weak damping oscillations with natural frequency in plasma current, radial electric fields and so on, detection of them is usually difficult. Its second effects are to cause some types of fluctuations in density and other plasma parameters at the edge of plasma. Such fluctuations have been observed in Damavand tokamak [4] . Probably, some fluctuations in kHz range in H mode of tokamak and in plasma edge can be related to the natural frequency discussed above. When the value of ![]() is constant no fluctuation would be seen and capacitive and inductive properties do not play an important role and the circuit in Figure 3 is changed to a simple resistive circuit.
is constant no fluctuation would be seen and capacitive and inductive properties do not play an important role and the circuit in Figure 3 is changed to a simple resistive circuit.
3. Results and Discussion
The experimental data of the Damavand tokamak are [10] :
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
, ![]() ,
, ![]() and the discharge time
and the discharge time![]() .
.
On the basis of dimension and condition of Damavand tokamak we would have:
![]() ,
,![]() ,
,![]() and
and![]() .
.
After some calculating it would be:![]() .
.
And, therefore, it would be: ![]() or
or![]() .
.
As previously noted, the first effect of the capacitance is weak damping oscillations with the frequency ![]() that is the common result of an RLC circuit. However, when the loop voltage is dc, oscillation would not observe. Usually during the disruption instability a negative spike would observe in loop voltage. Such spikes in loop voltage and the condition of
that is the common result of an RLC circuit. However, when the loop voltage is dc, oscillation would not observe. Usually during the disruption instability a negative spike would observe in loop voltage. Such spikes in loop voltage and the condition of ![]() in a tokamak leads to a solution for Equation (9) in the form of a weak damped oscillation
in a tokamak leads to a solution for Equation (9) in the form of a weak damped oscillation![]() .
.
In the experiments with Damavand tokamak that a sample of their results is demonstrated in Figure 4, when
the negative spike of loop voltage is observed, the disruption instability happened and ![]() showed weak
showed weak
damping oscillations. From the calculations using the presented model, it is seen that the frequency of these oscillations is approximately 100 kHz with damping in form of![]() . In Figure 4, the calculated signal by Equation (11) for an ideal shock input voltage is compared with experimental results and a good agreement between
. In Figure 4, the calculated signal by Equation (11) for an ideal shock input voltage is compared with experimental results and a good agreement between
them is observed [10] . ![]() is measured by a Rogowski coil.
is measured by a Rogowski coil.
When a power source (such as induced current, radio frequency wave, neutral beam) is injected into the plasma, there will be two working regimes:
1) The first one is a transient regime in which L and C along with R play role in equation of circuit and to simulate the behaviour of the plasma, using RLC circuit (Figure 3) with Equation (9) is necessary.
2) In the second regime that is a steady state regime, a simple resistive circuit with circuit equation of ![]() is sufficient.
is sufficient.
Therefore, the capacitance of the plasma like its inductance, plays important role in some working regimes of tokamak. The importance of capacitance properties is not limited to regimes with time-varying loop voltages. In
![]()
each transient regime and regimes with time varying power source (such as radio frequency waves and neutral beam heating) the effect of capacitive property can be seen. In Figure 3, in addition to an electrical power supply, radio frequency waves and neutral beams can be considered as the power supply.
4. Conclusions
The radial electric field in study of the H mode of tokamak plasmas is a very important parameter and several models have been proposed to explain the origin of them. In this paper, the effects of capacitive property on radial electric field in tokamak are briefly explained. It is proposed that a radial electric field is produced by a ra-
dial current in the form of ![]() [5] in which
[5] in which ![]() is the total current in the radial direction.
is the total current in the radial direction.
Then, a new model for equivalent circuit of tokamak plasmas on the base of capacitive property is explained. The plasma has the capacitive property of ![]() in all regions between its centre and the vacuum chamber wall. With respect to that value of
in all regions between its centre and the vacuum chamber wall. With respect to that value of ![]() inside the plasma is maximum, the capacitance between centre of plasma and its edge is very high .Therefore, the capacitance in Equation (7) should be estimated as the capacitance of the space between plasma edge and the vaccum chamber that generates a radial electric field on the plasma edge
inside the plasma is maximum, the capacitance between centre of plasma and its edge is very high .Therefore, the capacitance in Equation (7) should be estimated as the capacitance of the space between plasma edge and the vaccum chamber that generates a radial electric field on the plasma edge
in the form of![]() . We can investigate the generation of radial electric field in H mode using this
. We can investigate the generation of radial electric field in H mode using this
value for capacitance in Equation (8) and Figure 3 which gives more accurate results.
In this article, the analysis on the base of this model is first accomplished for Damavand tokamak and a good agreement between results of this model and the experimental results is observed. This model may be extended in future for analysis of the performance of big tokamaks such as ITER.