Estimated Bounds for Zeros of Polynomials from Traces of Graeffe Matrices ()
1. Introduction
Deriving zero bounds for polynomials is a classical problem that has been proven essential in various disciplines such as controling engineering problems, eigenvalue problems in mathematical physics, and digital audio signal processing problems―to name just a few [1] . Specially, a large number of research papers have given bounds of their moduli, e.g., well-known and classical bounds named after Cauchy, Montel and Kojima [2] [3] ; more advanced results can be found in [4] - [8] and references therein. Furthermore, bounds for the zeros of poly- nomials were needed in achieving some numerical computation methods, as providing information on the location of the zeros can be used to find initial guesses for iterative computation algorithms.
An estimated value of the largest moduli of the roots of a polynomial can be obtained as a limit of a sum of power of these roots using resultants [9] . However, it is well-known that computation of polynomials resultants is tedious and expensive; for this, we proceed by determining the trace of the Graffe matrix of order m of the polynomial P, which is exactly the sum of the m-th powers of the eigenvalues of the companion matrix of P. So we get our main result relying on Dandelin-Graeffe method to estimate the largest moduli bounds of the roots of P. This seems to be a significant progress compared to the use of resultants; moreover, it reveals a substantial convergence gain, teaming up with an approach used in [7] . This finding is rather significant in the large available methods used to improve the location of the zeros of polynomials.
The rest of the paper is organized as follows. In Section 2, we introduce the Graeffe matrix of a complex polynomial P and derive its trace from the classical Jordan normal form. In Section 3, we extend the Dandelin- Graeffe’s method to find the maximum moduli of the zeros of P, relying on the limit of Graeffe matrix’s trace of P. Through some examples, Section 3 illustrates that a few iterations of Graeffe’s matrix trace can give very tight bounds for the absolute value of the zeros of polynomials, with comparatively fast convergence.
2. Graeffe Polynomials and Graeffe Matrix’s Trace
For an n-dimensional matrix A, we call the spectrum of A the set of all its eigenvalues, denoted by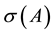 . Its spectral radius
. Its spectral radius 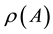 is defined by
is defined by 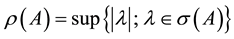 as the largest magnitude attained by any eigenvalue of A. Setting up the elements of
as the largest magnitude attained by any eigenvalue of A. Setting up the elements of 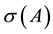 with their geometric and algebraic multiplicities, determines the eigenstructure of A. It’s well-known that all matrices similar to A have the same eigenstructure, specially we have the useful classical lemma [10] :
with their geometric and algebraic multiplicities, determines the eigenstructure of A. It’s well-known that all matrices similar to A have the same eigenstructure, specially we have the useful classical lemma [10] :
Lemma 1. A square complex matrix A of order n is similar to a block diagonal matrix

for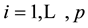 , each block
, each block 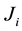 is a square matrix of order
is a square matrix of order 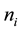 of the form
of the form

For ,
, 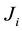 is called a “Jordan block” of
is called a “Jordan block” of 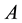 and
and 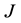 the Jordan normal form of
the Jordan normal form of .
.
Remark: The spectrum of a matrix 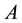 is identical with the spectrum of its Jordan normal form.
is identical with the spectrum of its Jordan normal form.
Lemma 2. If 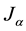 is a Jordan block of order
is a Jordan block of order ![]() of A with eigenvalue
of A with eigenvalue ![]() and m a positive integer, we have
and m a positive integer, we have
![]()
Proof. For arbitrary indices i and j, it is direct to verify the claim by using a proof by induction.
From the previous result, we deduce the two following corollaries:
Corollary 1. The m-th power of an n-dimensional matrix A is similar to the m-th power of its Jordan normal form as a direct sum of upper triangular matrices. Besides, each triangular block will consist of m-th power of its associate eigenvalue on the main diagonal.
Corollary 2. The trace of the m-th power of A is the sum of the m-th powers of the eigenvalues of A.
Definition 1. For ![]() a polynomial of degree d with complex coefficients, we will use the Frobenius companion matrix of
a polynomial of degree d with complex coefficients, we will use the Frobenius companion matrix of ![]() defined as
defined as
![]()
Let ![]() be a positive integer and
be a positive integer and![]() , then the Graeffe matrix of P of order m is defined as the m-th power of
, then the Graeffe matrix of P of order m is defined as the m-th power of![]() , and denoted by
, and denoted by![]() .
.
Definition 2. The characteristic polynomial of ![]() is called the Graeffe polynomial of P of order m, denoted by
is called the Graeffe polynomial of P of order m, denoted by![]() .
.
Remarks:
1) It can be computed also using resultants, as quoted in the following lemma ( [9] , Thàreme 3.1): assuming that P be a polynomial of degree d and![]() , then
, then![]() .
.
2) Relying on Proposition 1, it follows that for all![]() , there exists
, there exists ![]() products of square- matrices of order d; moreover, for k + d consecutive index, this number is
products of square- matrices of order d; moreover, for k + d consecutive index, this number is![]() . With comparatively using resultants, such computing time gain is shown through the following example (Table 1) done via the computer algebra system Maple (see Maple code in Appendix).
. With comparatively using resultants, such computing time gain is shown through the following example (Table 1) done via the computer algebra system Maple (see Maple code in Appendix).
Proposition 1. Let P be a polynomial of degree d with complex coefficients, then the trace of ![]() is exactly the sum of the m-th power of the zeros of P.
is exactly the sum of the m-th power of the zeros of P.
Proof. It is well-known that the eigenvalues are the zeros of the polynomial P; therefore, the result follows immediately from Corollary 2.
3. Estimation Method of Dandelin-Graeffe
Proposition 2. Let P be a polynomial of degree d with complex coefficients and ![]() as its zeros, such that
as its zeros, such that
![]()
There exists a sequence of polynomials ![]() such that
such that
![]()
the zeros of ![]() are the square of the zeros of
are the square of the zeros of ![]() and the
and the ![]() -power of those of P.
-power of those of P.
Proof. The basic technique to write down the proclaimed sequence of polynomials is done through an iteration refered to as the Dandelin-Graeffe method (see [6] ).
Starting with ![]() and
and![]() , we have
, we have
![]()
a polynomial of degree![]() , which zeros are the squares of the zeros of
, which zeros are the squares of the zeros of![]() .
.
For the induction process, one performs the following iteration
![]()
which transforms ![]() as
as ![]() which zeros are the squares
which zeros are the squares
of the zeros of![]() . As consequence, the zeros of
. As consequence, the zeros of ![]() are the
are the ![]() -power of those of
-power of those of![]() .
.
Lemma 3.
Let ![]() where
where ![]() are complex numbers such that
are complex numbers such that
![]() , then
, then
Proof. One can refer to [9] (Thèorème 1.4).
As a special case of Lemma 3, we can consider sequences of traces of![]() , the Graeffe matrix of P of order
, the Graeffe matrix of P of order![]() . By this way, we get a slight improvement of the bound for the absolute value of the unique largest zero of a polynomial; moreover, we can noticed a fast convergence of such sequence towards the expected value.
. By this way, we get a slight improvement of the bound for the absolute value of the unique largest zero of a polynomial; moreover, we can noticed a fast convergence of such sequence towards the expected value.
Proposition 3. Let ![]() be a polynomial of degree
be a polynomial of degree ![]() with complex coefficients such that
with complex coefficients such that
![]()
where ![]() are the zeros of
are the zeros of ![]() such that
such that![]() , then
, then
![]()
Remark: It is important to note that the existence of an unique dominant zero is essential to the validity of the previous result, as shown in ( [9] , p. 8). However, there is a more general result which doesn’t rely on neither the existence of a single dominant absolute value of the polynomial’s zero, nor the obligation to browse only terms whose indices are powers of 2. Such generalization, due to Mignotte and Ştefǎnescu [7] includes Lemma 3 as a special case; it can be stated as the following lemma:
Lemma 4. Let ![]() where
where ![]() such that
such that![]() , then
, then
![]()
Remark: Bearing in mind that there is no need to check the unicity of the largest modulus of the zero of a given ploynomial, a few iterations of d consecutive values of the traces ![]() of the Graffe matrices
of the Graffe matrices![]() , for an initial value of the exponant m sufficiently large, yields a good approximation of the maximum of moduli of the zeros of
, for an initial value of the exponant m sufficiently large, yields a good approximation of the maximum of moduli of the zeros of![]() .
.
Proposition 4.
Let ![]() be a polynomial of degree
be a polynomial of degree ![]() with complex coefficients such that
with complex coefficients such that
![]()
where ![]() are the zeros of
are the zeros of ![]() such that
such that![]() , then
, then
![]()
4. Numerical Results
1) We consider the polynomial
![]()
with an unique absolute value of dominant zero, namely 5. The application of the Graeffe’s zero-squaring method (Proposition 3) to the Graeffe’s polynomial of order ![]() yields the exact bound with comparatively little effort as the bound is attained from
yields the exact bound with comparatively little effort as the bound is attained from ![]() (Table 2).
(Table 2).
![]()
Table 2. Unique dominant bound via Graeffe’s zero-squaring method.
The previous result turns out as a considerably better bound, comparing with some classical explicit bounds gathered from Dehmer ( [4] , p. 1, 2), as shown in Table 3.
![]()
Table 3. Classical explicit bounds for ![]() (see [4] ).
(see [4] ).
2) Let ![]() be a polynomial with 7 as the largest zero.
be a polynomial with 7 as the largest zero.
By Proposition 4, few iterations of sequences of the maximum of ![]()
![]() ,
,
yield some sharp estimations of the real modulus of this double zero, for small values of m (Table 4).
![]()
Table 4. Computation of the largest (double) bound of![]() .
.
Moreover, the method leads to better results when locating explicit bounds for zeros of polynomials as shown in Table 5.
![]()
Table 5. Classical explicit bounds for ![]() (see [4] ).
(see [4] ).
3) Let’s now consider the polynomial ![]() with 6 as a triple dominant zero. As done in the previous example, dealing with Graeffe’s polynomial of
with 6 as a triple dominant zero. As done in the previous example, dealing with Graeffe’s polynomial of ![]() yields a quick com- putation of the value of dominant eigenvalue of Graeffe’s matrix of
yields a quick com- putation of the value of dominant eigenvalue of Graeffe’s matrix of ![]() (Table 6).
(Table 6).
![]()
Table 6. Estimation of the largest (triple) bound of![]() .
.
It’s important to notice that the convergence seems to become a bit slower than that in the previous case of the existence of a double dominant zero.
Moreover, the method leads to better results when locating explicit bounds for the zeros of polynomials (see Table 7).
![]()
Table 7. Classical explicit bounds for ![]() (see [4] ).
(see [4] ).
Acknowledgements
We would like to thank Professor Maurice Mignotte for his valuable suggestions and comments. We thank also the Editor and the anonymous referees for their comments.
Appendix: Maple Codes
Graeffegen := proc (![]() ,
,![]() ::integer)
::integer)
local![]() ;
;
if ![]() then print(''Error'')
then print(''Error'')
else G := sort(resultant![]() )
)
end if
end proc:
GraeffeMatrix := proc (![]() ,
,![]() ::integer)
::integer)
local![]() ;
;
![]() := CompanionMatrix
:= CompanionMatrix![]() ;
;
![]() := MatrixPower
:= MatrixPower![]() ;
;
sort(CharacteristicPolynomial![]()
end proc:
・ In Graeffegen, P is a polynomial in![]() . The output is the Graeffe polynomial of order k of P.
. The output is the Graeffe polynomial of order k of P.
・ In GraeffeMatrix, B = CompanionMatrix(P, X) stands for the CompanionMatrix of the polynomial ![]() and CharacteristicPolynomial
and CharacteristicPolynomial ![]() gives the characteristic polynomial of Bk.
gives the characteristic polynomial of Bk.