1. Introduction
A ring 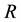 is symmetric if for any triple
is symmetric if for any triple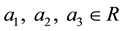 ,
,  then for any permutation
then for any permutation 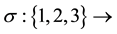

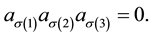 J. Lambek in [1] introduced symmetric rings, and got a characterization that a ring
J. Lambek in [1] introduced symmetric rings, and got a characterization that a ring 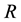 with one is symmetric if and only if
with one is symmetric if and only if 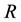 contains a subring which is isomorphic to the rings of sections of a sheaf of prime torsion free symmetric rings. Lambek also noticed that the symmetric property is a weaker notion than that of primeness (see [1: p. 362]). The class of symmetric rings lie between the classes of reduced and reversible rings and they have been extensively studied and generalized in various directions, for instance, some references are [2] - [4] , and [5] . Most of the studies on symmetric rings were carried over rings with identity. In this note we assume that rings, in general, are not equipped with the multiplicative identity. Let us say that a ring
contains a subring which is isomorphic to the rings of sections of a sheaf of prime torsion free symmetric rings. Lambek also noticed that the symmetric property is a weaker notion than that of primeness (see [1: p. 362]). The class of symmetric rings lie between the classes of reduced and reversible rings and they have been extensively studied and generalized in various directions, for instance, some references are [2] - [4] , and [5] . Most of the studies on symmetric rings were carried over rings with identity. In this note we assume that rings, in general, are not equipped with the multiplicative identity. Let us say that a ring 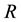 is right symmetric if for any triple
is right symmetric if for any triple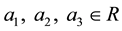 ,
,  , then
, then . Left symmetric rings are defined analogously. Some concrete examples are given here to show that right (as well as left) symmetric rings are different than symmetric rings. It is observed that, the Lambek criterion about symmetric rings with one, as given in [1] , can be extended to right (or left) symmetric rings with idempotents (Proposition 2.7).
. Left symmetric rings are defined analogously. Some concrete examples are given here to show that right (as well as left) symmetric rings are different than symmetric rings. It is observed that, the Lambek criterion about symmetric rings with one, as given in [1] , can be extended to right (or left) symmetric rings with idempotents (Proposition 2.7).
A weaker notion of symmetric is reversible which P.M. Cohn defined in [6] as: a ring  is reversible if for any
is reversible if for any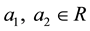 ,
, 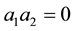 implies
implies ![]() In [7] , Anderson and Camillo defined that a ring
In [7] , Anderson and Camillo defined that a ring ![]() (may not be
(may not be
with 1) satisfies![]() , if for any
, if for any![]() , where
, where![]() , the product
, the product ![]() implies that the product
implies that the product![]() , where
, where![]() , is a permutation. Thus, in their terminology, if a ring satisfies
, is a permutation. Thus, in their terminology, if a ring satisfies
![]() , it is reversible, and if it satisfies
, it is reversible, and if it satisfies![]() , it is symmetric. They proved that
, it is symmetric. They proved that ![]() implies
implies![]() ,
, ![]() but the converse need not be true in general ([7] ; Example I-4).
but the converse need not be true in general ([7] ; Example I-4).
For a ring ![]() with
with![]() , clearly, every symmetric ring is reversible, but the converse may not be true, for instance, see ([7] ; Example 1-5). In ([8] : Example 7], Mark proved that the group ring
, clearly, every symmetric ring is reversible, but the converse may not be true, for instance, see ([7] ; Example 1-5). In ([8] : Example 7], Mark proved that the group ring ![]() where
where ![]() is the group of quaternions, is reversible but not symmetric. For a ring without one, a symmetric ring may not be reversible. For instance, for any ring A consider the ring of strictly upper triangular matrices
is the group of quaternions, is reversible but not symmetric. For a ring without one, a symmetric ring may not be reversible. For instance, for any ring A consider the ring of strictly upper triangular matrices ![]() Then
Then![]() ,
, ![]() , so
, so ![]() is symmetric.
is symmetric.
On the other hand one sees that if![]() , then
, then![]() , but
, but![]() . Hence
. Hence ![]() is not reversible. Thus by above fairly simple examples we firmly state that, for rings, in general,
is not reversible. Thus by above fairly simple examples we firmly state that, for rings, in general,
![]()
In Section 2, after definition, we gave some examples of right symmetric rings which are not symmetric, and developed some interactions with other classes of rings such as von Neuman regular, semicommutative, and Armendariz. In Section 3 we did some extensions of Klein 4-rings and a McCoy ring is constructed in the last section.
2. Right and Left Symmetric Rings
One notices that, in a ring without 1, and with ![]() implies that
implies that![]() , the commutation only appears on the last two elements. There is no guaranty that
, the commutation only appears on the last two elements. There is no guaranty that![]() , for the support of this claim we provide below some examples. So, let us define that:
, for the support of this claim we provide below some examples. So, let us define that:
Definitions 2.1. A ring ![]() is right (respt. left) symmetric if for any triple,
is right (respt. left) symmetric if for any triple, ![]() ,
, ![]() implies that
implies that ![]() (respt.
(respt.![]() ).
). ![]() is symmetric if
is symmetric if ![]() is both, left and right symmetric.
is both, left and right symmetric.
Examples 2.2. (1) Klein 4-rings. ([8] : Example 1] Consider the so called Klein-4 ring:![]() , which has two generators a and b, and is a Klein 4-group with respect to addition. Its characteristic is 2 and the relations among its elements are:
, which has two generators a and b, and is a Klein 4-group with respect to addition. Its characteristic is 2 and the relations among its elements are:
![]()
Let us consider all possible products of the three non-zero elements of V. There are total ![]() products, among them 15 are zero and 12 are non zero. Consider a typical product
products, among them 15 are zero and 12 are non zero. Consider a typical product ![]() of three nonzero elements
of three nonzero elements![]() . Then
. Then![]() , if either
, if either ![]() or
or![]() . This means that
. This means that![]() . So
. So ![]() is right symmetric. If
is right symmetric. If ![]() and
and![]() , then clearly
, then clearly![]() . For instance
. For instance ![]() but
but![]() . This implies that
. This implies that ![]() is not symmetric. (Erroneously it is mentioned in ([8] , Example 1]) that
is not symmetric. (Erroneously it is mentioned in ([8] , Example 1]) that ![]() is symmetric). Obviously, there is no question of reversibility as well, as
is symmetric). Obviously, there is no question of reversibility as well, as ![]() but
but![]() .
.
Similarly, the opposite ring, ![]() is left symmetric and is neither symmetric nor reversible. Both rings are not reduced also, because
is left symmetric and is neither symmetric nor reversible. Both rings are not reduced also, because ![]() is a non-zero nilpotent element.
is a non-zero nilpotent element.
(2) For any ring ![]() define the
define the ![]() -
- ![]() -column (respt. row) matrix ring, denoted by
-column (respt. row) matrix ring, denoted by ![]() (respt.
(respt.![]() , to be a subring, without identity, of the full matrix ring
, to be a subring, without identity, of the full matrix ring ![]() such that it has non-zero elements only in the
such that it has non-zero elements only in the ![]() -column (respt.
-column (respt. ![]() -row). In fact
-row). In fact ![]() (respt.
(respt.![]() ) is a left (respt. right) ideal of
) is a left (respt. right) ideal of![]() . Note that,
. Note that, ![]() is right symmetric if and only if
is right symmetric if and only if ![]() is right symmetric. Indeed, if we let
is right symmetric. Indeed, if we let ![]() to be right symmetric and
to be right symmetric and![]() , then
, then
![]()
The converse is obvious. Analogously, ![]() is left symmetric. Note that, if
is left symmetric. Note that, if ![]() is symmetric or even a commutative domain or a field,
is symmetric or even a commutative domain or a field, ![]() may not be symmetric. For instance, in
may not be symmetric. For instance, in ![]() if
if
we let![]() ,
, ![]() ,
, ![]() , then one can easily observe that
, then one can easily observe that ![]()
but![]() .
.
Similarly, ![]() is left symmetric and is not symmetric.
is left symmetric and is not symmetric.
(3) Let ![]() be any domain. Then the direct sum
be any domain. Then the direct sum ![]() and
and ![]() are right and left symmetric rings, respectively, under component wise addition and multiplication. Similarly,
are right and left symmetric rings, respectively, under component wise addition and multiplication. Similarly, ![]() and
and ![]() are right and left symmetric rings, respectively.
are right and left symmetric rings, respectively.
(4) In [5] Kwak defined left and right ![]() -symmetric rings as follows: Let
-symmetric rings as follows: Let ![]() be an endomorphism on a ring
be an endomorphism on a ring![]() . Then
. Then ![]() is right (respt. left)
is right (respt. left) ![]() -symmetric, if for any triple,
-symmetric, if for any triple, ![]() ,
, ![]() (respt.
(respt.![]() ). Thus right and left symmetric rings are special cases of right and left
). Thus right and left symmetric rings are special cases of right and left ![]() -symmetric rings, with
-symmetric rings, with![]() . It follows immediately from ([5] , Proposition 2.3(2)) that if a reversible ring is left (or right) symmetric, then it is symmetric. Note that in [5] rings are with identity.
. It follows immediately from ([5] , Proposition 2.3(2)) that if a reversible ring is left (or right) symmetric, then it is symmetric. Note that in [5] rings are with identity.
There is a symmetry between right and left symmetric rings, because a ring ![]() is right symmetric if and only if its opposite ring is left symmetric. So in the following we will only deal with right symmetric rings, left symmetric rings will appear when needed.
is right symmetric if and only if its opposite ring is left symmetric. So in the following we will only deal with right symmetric rings, left symmetric rings will appear when needed.
A ring R is said to be semicommutative as defined by Bell in [9] , if for any pair![]() ,
, ![]() then for all
then for all![]() ,
,![]() . There are several names of a semicommutative ring in literature. For historical remarks and other details we refer the reader to [10] . All reduced rings are symmetric and symmetric rings are semicommutative. The ring
. There are several names of a semicommutative ring in literature. For historical remarks and other details we refer the reader to [10] . All reduced rings are symmetric and symmetric rings are semicommutative. The ring ![]() in Example 2.2. is semicommutative (can be checked easily). A ring R is abelian if every idempotent
in Example 2.2. is semicommutative (can be checked easily). A ring R is abelian if every idempotent ![]() is central, duo if every right and left ideals are ideals, and reflexive if for any pair
is central, duo if every right and left ideals are ideals, and reflexive if for any pair![]() ,
, ![]() , then
, then![]() . A ring R is von Neumann regular if
. A ring R is von Neumann regular if![]() , there exists an
, there exists an![]() , such that
, such that![]() .
.
A right symmetric ring in general is non abelian, non duo, non reflexive, and not a von Neumann regular ring. We pose quick counter examples for these claims. The Klein 4-ring ![]() is right symmetric in which
is right symmetric in which ![]() is an idempotent. Because
is an idempotent. Because ![]() and
and![]() , so
, so ![]() is not central, so V is non abelian. In V,
is not central, so V is non abelian. In V, ![]() is a right ideal but
is a right ideal but ![]() means that
means that ![]() is not an ideal, so V is not right duo. Because
is not an ideal, so V is not right duo. Because ![]() but
but ![]() , hence V is not reflexive. Finally,
, hence V is not reflexive. Finally, ![]() , so V is not von Neumann regular.
, so V is not von Neumann regular.
It is defined in [11] that a ring ![]() with an involution
with an involution ![]() is
is ![]() -reversible, in case for every pair of elements
-reversible, in case for every pair of elements![]() , such that
, such that![]() , then
, then![]() .
.
There are several right symmetric rings without one which are symmetric. For instance, the ring of strictly upper triangular matrices over any ring is without one and is symmetric. Few more cases are given in the following:
Proposition 2.3. (1) Every symmetric ring is right symmetric and every right symmetric ring with one is sym- metric.
(2) Every reduced ring is right symmetric ( [1] : (G); [7] : Theorem I-3). Conversely, a right symmetric ring which is not symmetric cannot be reduced.
(3) Every right symmetric ring is semicommutative.
(4) Every von Neumann regular ring which is right symmetric is symmetric.
(5) Every reversible ring which is right symmetric is symmetric.
(6) Every ring with involution which is right symmetric is symmetric.
(7) Every ring with a reversible involution is right symmetric and hence symmetric.
(8) (1) - (7) all hold if we replace right by left.
Proof: (1) and (5) are obvious.
(2) Let a ring ![]() be reduced. Assume that for some
be reduced. Assume that for some![]() ,
, ![]() then
then ![]()
![]() this means that
this means that![]() . Hence
. Hence ![]() is right symmetric.
is right symmetric.
Conversely, let ![]() be right symmetric but not symmetric. Assume that
be right symmetric but not symmetric. Assume that ![]() such that
such that ![]() and
and ![]() but at least one of cab, cba, bac and bca is not equal to zero. Thus if
but at least one of cab, cba, bac and bca is not equal to zero. Thus if ![]() then
then![]() . Hence
. Hence ![]() is not reduced. If
is not reduced. If ![]() then
then![]() , so
, so ![]() But then
But then![]() .
.
(3) Let ![]() be a right symmetric ring. Assume that for any pair
be a right symmetric ring. Assume that for any pair![]() ,
,![]() . Then for all
. Then for all![]() , abr = 0. Hence
, abr = 0. Hence![]() , and so
, and so ![]() is semicommutative.
is semicommutative.
(4) Assume that ![]() is von Neumann regular and is right symmetric. Let
is von Neumann regular and is right symmetric. Let ![]() be such that
be such that![]() . Then for some
. Then for some![]() ,
,![]() . Then
. Then ![]() or
or![]() . Thus
. Thus ![]()
![]() we conclude that
we conclude that ![]() is reduced. Then by (2)
is reduced. Then by (2) ![]() is left symmetric, hence symmetric.
is left symmetric, hence symmetric.
(6) Let ![]() be a ring with an involution
be a ring with an involution![]() . This means that
. This means that ![]() is an anti-automorphism on
is an anti-automorphism on ![]() of order two. In addition, let
of order two. In addition, let ![]() be right symmetric. If
be right symmetric. If ![]() for some
for some ![]() then, because
then, because ![]() is right symmetric,
is right symmetric,![]() . Then
. Then ![]() or that because
or that because ![]() is right symmetric,
is right symmetric,![]() . By doubling the involution we get
. By doubling the involution we get ![]() which implies that
which implies that![]() . Again,
. Again, ![]() gives
gives![]() , and by the doubling of involution we get
, and by the doubling of involution we get ![]() and so the right symmetry gives
and so the right symmetry gives![]() .
.
(7) Let R be a ring with an involution ![]() and let
and let ![]() be
be ![]() -reversible. Now assume that
-reversible. Now assume that ![]() for some
for some ![]() Then
Then ![]() which gives
which gives ![]() or that
or that![]() . By similar techniques we get the remaining permutations equal to zero. So
. By similar techniques we get the remaining permutations equal to zero. So ![]() -reversible rings are right and left symmetric, hence symmetric.
-reversible rings are right and left symmetric, hence symmetric.
(8) holds by left and right symmetry. □
A quick consequence of Proposition 2.3 (6) is the following.
Corollary 2.4. Every right symmetric ring which is not symmetric cannot adhere to an involution.
Examples 2.5. Hence, ![]() and
and![]() , and their generalizations as discussed in Sections 3 & 4 cannot adhere to any involution.
, and their generalizations as discussed in Sections 3 & 4 cannot adhere to any involution.
2.6. Some minimalities: (1) ![]() and
and ![]() are smallest noncommutative rings (up to isomorphism). These are right and left symmetric, respectively. So the minimal noncommutative right (or left) symmetric rings are V and
are smallest noncommutative rings (up to isomorphism). These are right and left symmetric, respectively. So the minimal noncommutative right (or left) symmetric rings are V and![]() .
.
(2) Next higher order noncommutative rings are of order eight. So two minimal noncommutative symmetric rings are strictly upper and lower triangular matrix rings ![]() and
and![]() , respectively. Both are without identity and are not reversible (can be checked easily).
, respectively. Both are without identity and are not reversible (can be checked easily).
(3) ( [3] ; Example 2.6) A minimal non-commutative symmetric ring with identity is the ring![]() , in which addition and multiplication are defined by the rules:
, in which addition and multiplication are defined by the rules:
![]()
(see details in [3] ; Example 2.6). This ring has sixteen elements and is also reversible.
Reappearance of the Lambek Criterion: Lambek proved in [1] that a ring with one is symmetric if and only if it is isomorphic to the rings of sections of a sheaf of prime - torsion free symmetric rings. Following is an extension of it.
Proposition 2.7. A ring ![]() with an idempotent is right symmetric if and only if
with an idempotent is right symmetric if and only if ![]() contains a subring which is isomorphic to the rings of sections of a sheaf of prime - torsion free symmetric rings.
contains a subring which is isomorphic to the rings of sections of a sheaf of prime - torsion free symmetric rings.
Proof: “Only if”, is obvious, because a symmetric ring with 1 is a right symmetric ring with an idempotent. For “if”, consider that ![]() is right symmetric. Let
is right symmetric. Let ![]() be an idempotent. Then the corner ring
be an idempotent. Then the corner ring ![]() being a subring of
being a subring of ![]() is right symmetric and because
is right symmetric and because ![]() is the multiplicative identity, so
is the multiplicative identity, so ![]() becomes a symmetric ring. Rest follows from ( [1] : Corollary 1]. □
becomes a symmetric ring. Rest follows from ( [1] : Corollary 1]. □
A ring R is called Armendariz as introduced by Rege, S. Chhawchharia in [12] if for any pair of polynomials
![]() and
and ![]() in
in ![]() such that
such that![]() , then
, then ![]()
![]() ,
,
![]() . In this section we construct an Armendariz Boolean ring and a polynomial semicommutative ring.
. In this section we construct an Armendariz Boolean ring and a polynomial semicommutative ring.
The first part of the following lemma is proved by Nielsen in ( [13] ; Lemma 1]. The remaining relations are just tautologies.
Lemma 2.8. Let R be a right symmetric ring. Let ![]() and
and ![]() be two polynomials in
be two polynomials in
![]() such that
such that![]() . Then the following relations hold:
. Then the following relations hold:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
Theorem 2.9. Let R be a right symmetric ring. Let ![]() and
and ![]() be two polynomials
be two polynomials
in ![]() such that
such that ![]() If the coefficients of
If the coefficients of ![]() (or
(or![]() ) are idempotents, then
) are idempotents, then
![]()
Proof: Assume that the coefficients of ![]() are idempotents. If
are idempotents. If ![]() is idempotent, then by (2) of above lemma
is idempotent, then by (2) of above lemma
![]()
Now the coefficients in ![]() are of the form
are of the form![]() ,
,![]() . The induction step suggests that:
. The induction step suggests that:![]() ,
, ![]() then remove the term
then remove the term ![]() from this sum and
from this sum and
multiply the remaining sum by![]() , where
, where ![]() consecutively, and removing the zero terms until we get the last term
consecutively, and removing the zero terms until we get the last term![]() ,
, ![]() In this process the relation (4) of Lemma 2.8 is also involved to delete the unwanted terms. Hence we conclude that
In this process the relation (4) of Lemma 2.8 is also involved to delete the unwanted terms. Hence we conclude that![]() ,
, ![]() ,
, ![]() and
and![]() . If the coefficients of
. If the coefficients of ![]() are idempotents, then (1) and (3) of Lemma 2.8 are involved to prove the desired result. □
are idempotents, then (1) and (3) of Lemma 2.8 are involved to prove the desired result. □
Corollary 2.10. Let ![]() be a right symmetric Boolean ring. Then:
be a right symmetric Boolean ring. Then:
(1) ![]() is Armendariz.
is Armendariz.
(2) For every pair of polynomials ![]()
(3) For every pair of polynomials ![]() In other words,
In other words, ![]() is semicommutative.
is semicommutative.
Proof: (1) and (2) are followed from Theorem 2.9.
(3) Let ![]() and
and![]() . Then
. Then![]() ,
, ![]()
![]() Let
Let ![]() Then
Then![]() ,
, ![]()
![]()
![]() . Because all terms in the product of polynomials
. Because all terms in the product of polynomials![]() ,
, ![]() and
and ![]() are of the form
are of the form![]() ,we conclude that:
,we conclude that:![]() . □
. □
3. Some Extensions of Klein 4-Rings
Now we pose few more examples of one sided symmetric rings. These rings are extensions of ![]() and
and ![]() First result gives a criterion of all rings of order
First result gives a criterion of all rings of order ![]() as symmetric and non symmetric.
as symmetric and non symmetric.
Theorem 3.1. For any prime![]() , a ring
, a ring ![]() of order
of order ![]() is symmetric if and only if it is reversible. The non-symmetric ring is either left or right symmetric.
is symmetric if and only if it is reversible. The non-symmetric ring is either left or right symmetric.
Proof: It is known that up to isomorphism there are eleven rings of order![]() . These can be classified as commutative and non-commutative rings. The first statement trivially holds for commutative rings. There are nine commutative rings and the only non-commutative rings are:
. These can be classified as commutative and non-commutative rings. The first statement trivially holds for commutative rings. There are nine commutative rings and the only non-commutative rings are:
![]()
and its opposite ring
![]()
Both rings are of characteristic ![]() and can be verified that these are neither symmetric nor reversible. Note that the non-commutative rings S and
and can be verified that these are neither symmetric nor reversible. Note that the non-commutative rings S and ![]() of order
of order![]() , for all primes
, for all primes![]() , are right symmetric and left symmetric, respectively. For instance, in case of S, the non-zero elements of S are of the form
, are right symmetric and left symmetric, respectively. For instance, in case of S, the non-zero elements of S are of the form![]() ,
, ![]() and
and![]() , where
, where![]() , so as in the case of
, so as in the case of![]() ,
,
![]()
Hence ![]() is right symmetric. But
is right symmetric. But ![]() is not symmetric, because
is not symmetric, because
![]()
Clearly ![]() is not reversible as well. □
is not reversible as well. □
Let ![]() be a set of symbols and consider the additive group
be a set of symbols and consider the additive group ![]() generated by these symbols. This group has
generated by these symbols. This group has ![]() elements. Define the multiplication on
elements. Define the multiplication on ![]() by the rule:
by the rule: ![]()
![]() Then clearly,
Then clearly,
![]()
These rules clearly imply that ![]() is an associative ring without 1 and is of characteristic 2. Let us denote this ring by
is an associative ring without 1 and is of characteristic 2. Let us denote this ring by ![]() as its order is
as its order is![]() . The Klein-4 ring
. The Klein-4 ring ![]() as discussed in Example 2.2 above is
as discussed in Example 2.2 above is ![]() and is smallest in the series.
and is smallest in the series.
Theorem 3.2. The ring ![]() is right symmetric but not left symmetric. Likewise,
is right symmetric but not left symmetric. Likewise, ![]() is left symmetric but not right symmetric.
is left symmetric but not right symmetric.
Proof: Assume that![]() , such that
, such that![]() . If any one of
. If any one of![]() , or
, or ![]() is zero, then we are done. So consider only non-zero elements.
is zero, then we are done. So consider only non-zero elements.
Assume that![]() ,
, ![]() and
and![]() , where
, where ![]() and
and ![]() such that
such that
![]() .
.
Note that for any ![]() and
and ![]() as above,
as above,
![]()
Same will be the consequences if we replace ![]() by
by![]() , i.e.
, i.e.
![]()
and
![]()
So ![]() if and only if either
if and only if either ![]() is even or
is even or ![]() is even. This means that
is even. This means that![]() . Hence
. Hence ![]() is right symmetric.
is right symmetric.
On the other hand, assume that ![]() is even. Because
is even. Because ![]() and
and ![]() are odd, then
are odd, then![]() , but
, but![]() . This completes the proof.
. This completes the proof.
The second part can be obtained by symmetry. □
Trivial extension of a ring: Let ![]() be any ring, a trivial extension
be any ring, a trivial extension ![]() of
of![]() , is a subring of the upper triangular matrix ring over
, is a subring of the upper triangular matrix ring over ![]() and is defined as:
and is defined as:
![]()
Theorem 3.3. The trivial extension ring ![]() is a right symmetric ring where
is a right symmetric ring where ![]() is the Klein 4-ring.
is the Klein 4-ring.
Proof: In short we write ![]() as an element of
as an element of ![]() but we will follow the rule of matrix multiplication on such ordered pairs. So let
but we will follow the rule of matrix multiplication on such ordered pairs. So let![]() ,
, ![]() with
with![]() , where
, where![]() ,
,![]() . Then
. Then
(a) ![]() and
and
(b) ![]()
We want to prove that![]() . For this we need to establish that
. For this we need to establish that
(c) ![]() and that
and that
(d) ![]()
As in Example 2.2, (a) holds if either ![]() or
or![]() . Assume that
. Assume that ![]() and
and![]() , Then (b) holds if
, Then (b) holds if![]() . We substitute
. We substitute ![]() in (c) and (d). We see that these are also satisfied.
in (c) and (d). We see that these are also satisfied.
If ![]() and
and![]() , then (b) holds if
, then (b) holds if![]() . Again we substitute
. Again we substitute ![]() in (c) and (d), we see that these are satisfied. If
in (c) and (d), we see that these are satisfied. If![]() , then all
, then all ![]() are satisfied. Hence we conclude that
are satisfied. Hence we conclude that ![]() is right symmetric. □
is right symmetric. □
Remarks 3.4. (1) ![]() is not symmetric, as one can easily work out that
is not symmetric, as one can easily work out that
![]() ,
,
but
![]()
(2) It is known that if ![]() is reduced then
is reduced then ![]() is symmetric ([8] ; Corollary 2.4). Note that
is symmetric ([8] ; Corollary 2.4). Note that ![]() is not a reduced ring.
is not a reduced ring.
(3) The ring of ![]() upper triangular matrices over
upper triangular matrices over![]() ,
, ![]() is not right symmetric, because for
is not right symmetric, because for![]() ,
,
![]()
and
![]()
Thus, in general, ![]() or
or ![]() are not right symmetric. Hence, being right symmetric is not Morita invariant.
are not right symmetric. Hence, being right symmetric is not Morita invariant.
Theorem 3.5. For a commutative indeterminate![]() , the polynomial ring
, the polynomial ring ![]() is right symmetric.
is right symmetric.
Proof: Because ![]() is without 1, so
is without 1, so ![]() is also without 1 and so
is also without 1 and so![]() . Now let
. Now let![]() ,
, ![]()
![]() where ai, bj,
where ai, bj, ![]()
![]() ,
, ![]()
![]() , and assume that
, and assume that
![]()
where
![]()
Also assume that
![]()
where
![]()
We want to prove that if![]() , then so is
, then so is![]() . So assume that
. So assume that![]() . Then
. Then![]() ,
, ![]() , and these terms can be expressed as
, and these terms can be expressed as
![]()
where ![]() For
For![]() , we want to establish that
, we want to establish that![]() ,
, ![]() , where
, where
![]()
(I) We have five options for![]() . These are
. These are![]() ,
, ![]() ,
, ![]() ,
, ![]() , or
, or ![]() Any one choice will give us
Any one choice will give us![]() .
.
(II) Let![]() . From (I) if we choose
. From (I) if we choose![]() , then
, then![]() , and so
, and so![]() . For
. For![]() , we again have five choices,
, we again have five choices, ![]() or
or![]() , and with the previously chosen
, and with the previously chosen![]() , we see that
, we see that ![]()
(III) Let us have ![]() as in (I) & (II). Then
as in (I) & (II). Then ![]() Here again we have five choices for
Here again we have five choices for ![]() and
and ![]() For every choice we have
For every choice we have ![]() which implies
which implies ![]() and again we have five options here, each gives
and again we have five options here, each gives ![]() Thus we find that
Thus we find that ![]() holds. The choices for
holds. The choices for ![]() or
or ![]() will yield same result.
will yield same result.
(IV) Now assume that![]() . This is in continuation of (I), (II), & (III) and the same repetition will give us
. This is in continuation of (I), (II), & (III) and the same repetition will give us ![]() and
and ![]() simultaneously.
simultaneously.
The rest are similar.
Definitely, we need to watch the situation for non-zero values, for instance, if we let ![]()
![]() and
and ![]() then we see that
then we see that![]() ,
, ![]() Same situation comes if we let
Same situation comes if we let ![]() and
and![]() . Hence the required result is obtained. □
. Hence the required result is obtained. □
4. McCoy Rings without Identity
In [13] , Nielsen defined that a ring ![]() is a right McCoy, if
is a right McCoy, if![]() , then there exists an
, then there exists an![]() , such that
, such that![]() . Left McCoy and McCoy rings are defined similarly. It is proved in ( [13] , Theorem 2), that: every reversible ring is left and right McCoy, hence McCoy.
. Left McCoy and McCoy rings are defined similarly. It is proved in ( [13] , Theorem 2), that: every reversible ring is left and right McCoy, hence McCoy.
In ( [13] ; Section 3), Nielsen, constructed an example of a right McCoy ring with identity. This example is neither symmetric nor reversible, and there is no question that it is right or left symmetric because it has identity.
In next result we prove that the right symmetric ring ![]() is a right McCoy ring without identity.
is a right McCoy ring without identity.
Theorem 4.1. The ring ![]() as constructed in Theorem 2.2. is a McCoy ring.
as constructed in Theorem 2.2. is a McCoy ring.
Proof: Again, let ![]() be a set of symbols and consider the additive group
be a set of symbols and consider the additive group ![]() generated
generated
by these symbols and define the multiplication on ![]() by the rule:
by the rule: ![]()
![]()
Then ![]() is a ring as constructed in Theorem 2.3. The characteristic of this ring is 2. Consider an element of
is a ring as constructed in Theorem 2.3. The characteristic of this ring is 2. Consider an element of
the form![]() , where
, where![]() ,
, ![]() , and
, and ![]() is even and let all zk be distinct so that
is even and let all zk be distinct so that![]() . Then for any element
. Then for any element![]() ,
,![]() .
.
Assume that ![]() and
and ![]() be elements of
be elements of![]() , with
, with ![]() Then
Then
![]() Hence
Hence ![]() is right McCoy.
is right McCoy.
On the other hand, note that ![]() provided that the coefficients of
provided that the coefficients of ![]() are the elements of
are the elements of ![]()
of the form![]() , where
, where ![]() and
and ![]() is even. Hence for any
is even. Hence for any![]() ,
, ![]() which shows that
which shows that ![]()
is left McCoy. Hence ![]() is McCoy. □
is McCoy. □
Remarks 4.2. It follows from above that
(i) ![]() is McCoy, right symmetric, and semicommutative, but neither symmetric nor reversible.
is McCoy, right symmetric, and semicommutative, but neither symmetric nor reversible.
(ii) ![]() is McCoy, left symmetric, and semicommutative, but neither symmetric nor reversible.
is McCoy, left symmetric, and semicommutative, but neither symmetric nor reversible.
Example 4.3. In Section 3 of [14] an example of a McCoy ring is constructed such that its power series ring is not McCoy. Here we prove that the power series ring of Klein 4-ring, which we already have proved that it is
McCoy, is also McCoy. A typical element of ![]() is of the form
is of the form![]() ,
,
where ![]() is a coefficient in the power series ring
is a coefficient in the power series ring![]() . Clearly
. Clearly![]() ,
, ![]() , so
, so![]() . On
. On
the other hand, let ![]() and
and ![]() but
but![]() . Then the coefficients
. Then the coefficients ![]() in
in ![]() are in
are in
the set ![]() and as previously we got the outcome
and as previously we got the outcome![]() . Hence we conclude that
. Hence we conclude that ![]() is McCoy.
is McCoy.
We end up at a general statement. The following corollary can be proved by the methods used in Theorem 4.1.
Corollary 4.4. The power series ring ![]() is McCoy.
is McCoy.
Acknowledgements
This project was funded by the ISR, Umm Al-Qura University, under Grant No: 43305007. The authors, therefore, acknowledge with thanks the financial and technical support provided by ISR.