Semi-Analytical Solution of the 1D Helmholtz Equation, Obtained from Inversion of Symmetric Tridiagonal Matrix ()
1. Introduction
We focus on the inverse of the matrix (M) defined in the Equation (1) below. We are interested in applications of this matrix, because the latter allows solving many important differential equations in science and technology, especially mathematics, physics, engineering, chemistry, biology and other disciplines. The formula of the inverse of (M) was determined in [1] . But in this study, a different approach is presented with a rigourus and complete discussion of its regularity and complement, discussing the regularity of the matrix in great detail. In addition, the inverse of the antisymmetric tridiagonal matrix is determined analytically.
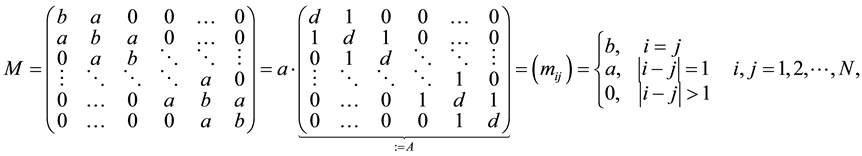 (1)
(1)
where, 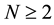 ,
, 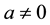 , and
, and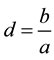 . In case where
. In case where  is zero, the inversion of the matrix (M) presents no difficulty.
is zero, the inversion of the matrix (M) presents no difficulty.
So we will focus on the matrix (A) and we will determine the exact form of its inverse, (B). We proceed as follows: first, we determine the determinant of (A) and give a very detailed discussion of its invertibility. Therefore, we formulate its inverse analytically and exactly. Then, we solve the Helmholtz equation, with the finite difference method, using the obtained inverse matrix. Additionally, we treat the skew-symmetric tridiagonal matrix and give the formula of its inverse.
2. Determinant of the Matrix (A)
2.1. Characteristic Equation and Discriminant 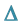
The calculation of the determinant of (A) and the discussion of the existence of its inverse constitute a very important part of this work. The determinant of (A) depends on N and is denoted . We define
. We define 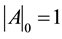 and
and . We also define
. We also define 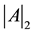 as follows:
as follows:
 (2)
(2)
By developing the determinant 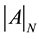 with respect to the first row, one finds that it follows a second-order linear homogeneous recurrence relation with constant coefficients [2] [3] :
with respect to the first row, one finds that it follows a second-order linear homogeneous recurrence relation with constant coefficients [2] [3] :
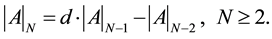 (3)
(3)
The term 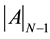 is the determinant of the submatrix of (A), obtained by eliminating its first row and its first column.
is the determinant of the submatrix of (A), obtained by eliminating its first row and its first column.  denotes the determinant of the submatrix of order N − 2, obtained by deleting the first two rows and first two columns of (A).
denotes the determinant of the submatrix of order N − 2, obtained by deleting the first two rows and first two columns of (A).
The characteristic equation of the recurrence relation, given by the Equation (3), is:
 (4)
(4)
The resolution of this Equation (4) yields the expression of ![]() in terms of N.
in terms of N.
The solutions of the characteristic equation are determined by the sign of the discriminant![]() .
.
2.2. Case![]() :
: ![]()
The discriminant is zero for two values of![]() :
: ![]() or
or![]() . For this case, the characteristic equation admits one double real solution:
. For this case, the characteristic equation admits one double real solution:![]() . Then, the general expression of the determinant is:
. Then, the general expression of the determinant is:
![]() (5)
(5)
where A' and B' are two constants which are determined taking into account the first two terms of the sequence![]() . The constant A' is obtained by considering:
. The constant A' is obtained by considering:
![]() (6)
(6)
The constant B' is determined in the following manner:
![]() (7)
(7)
So the determinant of the matrix (A), in the case where![]() , is given by the following formula:
, is given by the following formula:
![]() (8)
(8)
The Equation (8) is the exact formula of![]() , when the discriminant of the characteristic equation is zero. One remarks that, in this case, the matrix (A) is regular: its inverse exists. This regularity of (A) can be deduced from the expression of
, when the discriminant of the characteristic equation is zero. One remarks that, in this case, the matrix (A) is regular: its inverse exists. This regularity of (A) can be deduced from the expression of![]() . Because N is positive and therefore, the determinant cannot vanish.
. Because N is positive and therefore, the determinant cannot vanish.
2.3. Case![]() :
: ![]()
It corresponds to the case where![]() . Then, the characteristic Equation (4) has two distinct real solu- tions:
. Then, the characteristic Equation (4) has two distinct real solu- tions:
![]() (9)
(9)
The general expression of the determinant is for this case:
![]() (10)
(10)
The constants A' and B' can be determined, considering the values of ![]() for the first two orders: 0 and 1. One gets:
for the first two orders: 0 and 1. One gets:
![]() (11)
(11)
It holds:
![]() (12)
(12)
Thus, the determinant of (A) is obtained:
![]() (13)
(13)
This equation is equivalent to:
![]()
The determinant of (A) is different from zero, for the considered case![]() . Then, the tridiagonal symmetric matrix (A) is regular and its inverse exists. The remarkable Equation (14) gives the determinant of the matrix (A) in the case where the discriminant of the characteristic equation,
. Then, the tridiagonal symmetric matrix (A) is regular and its inverse exists. The remarkable Equation (14) gives the determinant of the matrix (A) in the case where the discriminant of the characteristic equation, ![]() , is strictly positive. One can verify, for example, that for
, is strictly positive. One can verify, for example, that for ![]() and
and![]() , we get
, we get![]() . This value can be obtained with Equation (14) or directly.
. This value can be obtained with Equation (14) or directly.
An observation of the determinant, for this case, allows another formulation of the formula in Equation (14). Because, one remarks that the determinant is a polynomial and can be developed. It holds:
![]() (14)
(14)
From the analysis of these polynomial expressions, one can demonstrate using mathematical induction that the determinant given by the Equation (14) can be formulated as follows:
![]() (15)
(15)
where [N/2] est equivalent to (N div 2). This latter formula in Equation (15) is given in [1] . But, we prefer the formulation of Equation (14) for two reasons.
The first is that we look for a matrix inverse. Then, it is important to know about the annulation of the determinant. Choosing the Equation (15) means that we have to search the zero of the polynomials, to know the invertibility of the matrix. While the Equation (14) shows clearly that the determinant does not vanish and thus, the matrix (A) is regular.
The second reason to prefer Equation (14) to Equation (15) is that programming the Equation (14) is more confortable than programming Equation (15). Because the latter needs loops for the sum, and it also needs recursions for the binomial coefficients.
2.4. Case![]() :
: ![]()
It corresponds to the case where![]() . Then, the characteristic Equation (4) admits two complex conjugate solutions:
. Then, the characteristic Equation (4) admits two complex conjugate solutions:
![]() (16)
(16)
These solutions ![]() and
and ![]() belong to the complex unit circle. Because their magnitude is equal to unity:
belong to the complex unit circle. Because their magnitude is equal to unity:![]() . Therefore, they can be written in the following manner:
. Therefore, they can be written in the following manner:
![]() (17)
(17)
with
![]() (18)
(18)
Then, the general expression of ![]() is:
is:
![]() (19)
(19)
The constants A' and B' are determined considering ![]() and
and![]() .
.
![]() (20)
(20)
One obtains the following relation that gives the determinant of (A), in the case where![]() :
:
![]()
Regularity of the Matrix (A) for ![]()
In this case, the regularity of (A) has to be studied. One solves:
![]() (21)
(21)
This Equation (21) admits N solutions ![]() that nullify the determinant of the matrix (A). These solutions are:
that nullify the determinant of the matrix (A). These solutions are:
![]() (22)
(22)
For these values of![]() , corresponding to
, corresponding to![]() , the determinant of the matrix (A) is zero and therefore its inverse does not exist. This result is very interesting. Because it shows that the eigenvalues
, the determinant of the matrix (A) is zero and therefore its inverse does not exist. This result is very interesting. Because it shows that the eigenvalues ![]() of the matrix can be expressed in the following manner:
of the matrix can be expressed in the following manner:
![]() (23)
(23)
In the treated case![]() , the inverse of the matrix (A) does not exist for
, the inverse of the matrix (A) does not exist for
![]() . So any formulation of the inverse for the considered case should ex-
. So any formulation of the inverse for the considered case should ex-
clude sub-cases where ![]() takes one of the values
takes one of the values![]() . Because for such values of
. Because for such values of![]() , the matrix (A) is not regular.
, the matrix (A) is not regular.
Special Case d = 0
This corresponds to![]() . In this case, we have:
. In this case, we have:![]() ; so
; so![]() . The determinant of the matrix (A) is:
. The determinant of the matrix (A) is:
![]() (24)
(24)
The Equation (24) is a very interesting result. First, it gives the exact formula of determinant for the case where ![]() is zero. In addition, it shows that the matrix for this case is regular for even
is zero. In addition, it shows that the matrix for this case is regular for even![]() , and non-reversible for odd
, and non-reversible for odd![]() . So, we can always guarantee the existence of the inverse matrix (A), taking an even number of mesh nodes
. So, we can always guarantee the existence of the inverse matrix (A), taking an even number of mesh nodes![]() . What deserves to be emphasized is that for odd
. What deserves to be emphasized is that for odd![]() , 0 is an eigenvalue of the matrix (A).
, 0 is an eigenvalue of the matrix (A).
![]() (25)
(25)
This closes the discussion of the determinant of a symmetric tridiagonal matrix, similar to the (M). All cases were studied in a very detailed manner. In each of these cases, the exact value of the determinant of (A) is given and its regularity has been widely discussed.
3. Inverse of the Matrix A
Before starting the determination of the inverse of the matrix (A), it is appropriate to discuss its properties. The symmetries of (A) will be found in its inverse (B).
First, the matrix (A) is symmetric:![]() . So its inverse is symmetric:
. So its inverse is symmetric:![]() . In addition, (A) is persymmetric i.e. it is symmetrical in relation to its anti-diagonal. This property also appears in its inverse, (B):
. In addition, (A) is persymmetric i.e. it is symmetrical in relation to its anti-diagonal. This property also appears in its inverse, (B):![]() .
.
These two properties show that the matrix (B) is determined when one fourth of its elements is known.
Determining (B) means to determine the cofactor matrix of (A). While these cofactors are obtained using determinants of submatrices of (A), it is not difficult to determine them. Because, a detailed work has been done in the previous section, concerning the determinant of (A) and its submatrices.
Thus, it is easy to see that:![]() . In the same way, it holds:
. In the same way, it holds:![]() . One has
. One has![]() ; and for every element of the first line of (B), we have:
; and for every element of the first line of (B), we have: ![]() and:
and:
![]() (26)
(26)
So the first and last lines, and also the first and last columns of the matrix (B) are known exactly using the symmetry and the persymmetry matrix (A).
We remember the previous section gives the formulas of all the determinants![]() .
.
The matrix (B) being the inverse of (A), its components satisfy the following relations:
![]() (27)
(27)
where ![]() is the Kronecker’s delta.
is the Kronecker’s delta.
From the first line of Equation (27), it is possible to obtain the second column of the matrix (B) from the first column, which is already known. Then, with the symmetry of the matrix (B), we have:
![]() (28)
(28)
With the symmetry and the persymmetry of (B), we also have:
![]() (29)
(29)
The second line of Equation (27) allows to find the elements of the third row and the third column of the matrix (B):
![]() (30)
(30)
Considering the Equation (28), the following relation is obtained:
![]() (31)
(31)
The second line of Equation (27) also allows to find the elements of the fourth row and the fourth column of (B):
![]() (32)
(32)
Considering the Equations (28) and (31), the following relation is obtained:
![]() (33)
(33)
The analysis of each element of the matrix (B) leads to the complete and exact formulation of this remarkable matrix:
![]() (34)
(34)
The Equation (34), combined with the Equation (26), gives:
![]() (35)
(35)
The Equation (35) determines all the elements of the upper triangle of the matrix (B). So the symmetry of the matrix allows to get the closed form of (B), inverse of the symmetric tridiagonal the matrix (A). Thus, (B) is known and each of its components is given by the following equation:
![]()
This beautiful relations is very important. It is an interesting result to solve any differential equation whose discretization leads to algebraic equations of the form![]() . It is clear that effective solutions for such equations exist. But, the exact formulation of this matrix (B) allow us to avoid inversion methods that use the RHS.
. It is clear that effective solutions for such equations exist. But, the exact formulation of this matrix (B) allow us to avoid inversion methods that use the RHS.
However, it deserves to be precised that the formula of the Equation (36) is not new. Indeed, it has already been determined in [1] . But the present study follows another approach and additionally provides a deeper and complete discussion of the regularity of (A): this work completes the study in [1] .
As application, we will solve the Helmholtz equation, which is a very important equation in physics, using the matrix (B). We could also take the equation of heat diffusion and the Poisson equation. But we prefer the former, which corresponds to the wave equation for harmonic excitation.
4. Application with the Resolution of Helmholtz Equation
Knowing the matrix (B) allows to solve all the boundary problems posed in following manner:
![]() (36)
(36)
![]() is a scalar field that obeys to the Helmholtz equation (or to the harmonic heat diffusion equation). This latter corresponds to the wave equation for harmonic excitation. The boundary conditions are of first kind: Dirichlet-Dirichlet i.e.
is a scalar field that obeys to the Helmholtz equation (or to the harmonic heat diffusion equation). This latter corresponds to the wave equation for harmonic excitation. The boundary conditions are of first kind: Dirichlet-Dirichlet i.e. ![]() and
and![]() . The RHS,
. The RHS, ![]() , is a specified function. The constant k is also known.
, is a specified function. The constant k is also known.
We consider an one-dimensional mesh with N + 2 discrete points![]() . Each point
. Each point ![]() is defined by
is defined by![]() , where
, where ![]() being the step size. We define
being the step size. We define![]() ,
, ![]() ,
,![]() .
.
The application of the finite difference method to the Equation (36), with the centered difference approxi-
mation![]() , leads to the following algebraic system of equations [4] - [6] :
, leads to the following algebraic system of equations [4] - [6] :
![]() (37)
(37)
where![]() .
.
Thus, one gets in matrix form
![]() (38)
(38)
where the vector ![]() is defined by:
is defined by:
![]() (39)
(39)
Thus, it holds![]() . The solution
. The solution ![]() at point
at point ![]() is given by a simple matrix-vector multiplication:
is given by a simple matrix-vector multiplication:
![]() (40)
(40)
This can be expressed in the following form
![]() (41)
(41)
which gives finally:
![]() (42)
(42)
This Equation (42) gives the solution ![]() at mesh point
at mesh point![]() .
.
One can also define
![]() (43)
(43)
Then, each element ![]() of the matrix (B) is given by:
of the matrix (B) is given by:
![]() (44)
(44)
Thus, each solution ![]() at point
at point ![]() can be written:
can be written:
![]() (45)
(45)
The Equations (42) and (45) are two forms of solution of the Helmholtz equation. Each of these two forms can be implemented simply and elegantly in a source code.
5. Numerical Results the Different Cases
The different studied cases are considered to illustrate the efficient of the proposed approach that is based on the exact inversion of the important matrix (A). Logically, this method is stable robust and very accurate. Because the method of inversion does not use the RHS of the differential equation.
For applications the value ![]() and
and ![]() have been chosen.
have been chosen.
The relative error ![]() at each point
at each point ![]() is defined by the following relation:
is defined by the following relation:
![]() (46)
(46)
The average relative error![]() , is computed, according the formula:
, is computed, according the formula:
![]() (47)
(47)
5.1. Results for![]() :
: ![]()
Sub-Case ![]() and
and ![]()
The sub-case where ![]() is considered. This corresponds to
is considered. This corresponds to ![]() and the differential equation becomes the Poisson’s one; which we discussed in [1] [4] . Here, we chose
and the differential equation becomes the Poisson’s one; which we discussed in [1] [4] . Here, we chose![]() .
.
The results are presented in the Table 1.
It holds, for the considered case:![]() .
.
Sub-Case ![]() and
and ![]()
For this sub-case, we have![]() . The constante
. The constante ![]() is different from zero and is:
is different from zero and is:![]() . The differential
. The differential
equation can be an Helmholtz or an Heat Diffusion’s equation or any other differential equation, discribed by Equation (37).
The results are presented in the Table 2, with![]() .
.
This results are very accurate and the average relative error is:![]() . One remarks that it more accurate than the previous case, which dealt with an elliptic equation: the Poisson’s one.
. One remarks that it more accurate than the previous case, which dealt with an elliptic equation: the Poisson’s one.
5.2. Results for![]() :
: ![]()
The Equation (14) gives the formula of the determinant![]() . Taking
. Taking![]() , one gets:
, one gets:![]() . Then, the results, given by the Table 3, are obtained for
. Then, the results, given by the Table 3, are obtained for![]() :
:
The average relative error is:![]() .
.
5.3. Results for![]() :
: ![]()
Results for![]() :
: ![]()
As discussed previously, an even ![]() is adequate for this case. We have chosen N = 100. Of course, and we have
is adequate for this case. We have chosen N = 100. Of course, and we have ![]() in order to get
in order to get![]() . The results are shown in the Table 4.
. The results are shown in the Table 4.
The average relative error is:![]() .
.
Results for ![]() and
and ![]()
We have chosen![]() ,
,![]() . Thus, we get
. Thus, we get![]() . The obtained results are shown in the Table 5 below.
. The obtained results are shown in the Table 5 below.
The average relative error is:![]() .
.
Results for ![]() and
and ![]()
Here, we chose![]() ,
,![]() . Thus, we get
. Thus, we get![]() . The obtained results are shown in the Table 6.
. The obtained results are shown in the Table 6.
The average relative error is:![]() .
.
6. Inverse of the Tridiagonal Antisymmetric (Skew-Symmetric) Matrix
We give here, additionally, the inverse of the tridiagonal antisymmetric matrix:
![]() (48)
(48)
Arguing as we did with the matrix (A), we get the characteristic equation to obtain the determinant of![]() :
:
![]() (49)
(49)
The discriminant ![]() and is strictly positive. Thus, the determinant of
and is strictly positive. Thus, the determinant of ![]() has the same form as the Equation (14), with the corresponding discriminant of the characteristic equation for
has the same form as the Equation (14), with the corresponding discriminant of the characteristic equation for![]() :
: ![]() :
:![]() ,
, ![]() , and for
, and for![]() , it holds:
, it holds:
![]()
One can remark that ![]() is regular for any value of
is regular for any value of ![]() different from zero. if
different from zero. if ![]() is zero and N is odd, then the inverse of
is zero and N is odd, then the inverse of ![]() does not exist.
does not exist.
Then, the inverse of ![]() that we denote
that we denote ![]() is given by the following relation:
is given by the following relation:
![]()
The corresponding applications for the inverse matrix ![]() are differential equations whose discretization leads to algebraic equations of the form
are differential equations whose discretization leads to algebraic equations of the form![]() .
.
7. Conclusion
This study has given the semi-analytical solution of each equation differential whose discretization leads to algebraic equations of the form![]() . The existence of the inverse of the discretization matrices is widely discussed. The presented approach is stable and gives very accurate results. The considered boundary problems are Dirichlet type.
. The existence of the inverse of the discretization matrices is widely discussed. The presented approach is stable and gives very accurate results. The considered boundary problems are Dirichlet type.