Evaporation Induced Thermal Patterns in Fluid Layers: A Numerical Study ()
1. Introduction
Thermal and/or solutal patterning of evaporating fluid layers is becoming an intriguing field of research for its promising applicability in many industrial applications, including the rapidly expanding domain of bio-tech- nology [1] and tissue engineering [2] . Also, compact, enhanced heat exchangers for cooling of micro-electronics often take advantage of the intrinsic endothermic character of the evaporation process. Despite the relatively great number of theoretical models [3] -[5] and semi-empirical assessments, the evaluation of the actual heat and mass transfer rate for fluid layers evaporating in presence of a flow of inert gas is still an open domain of investigation. As a matter of fact, at the interface of the evaporating layers, the gas flow induces an additional shear stress that couples with the thermo-capillary one induced by the evaporation process. This coupling can alter significantly the thermo-fluid-dynamic field at the interface, hence change the heat and mass transfer rate. To the best of our knowledge, many studies have been devoted both to thermo-capillary convection [6] and evaporation of a volatile liquid in presence of a still inert gas [7] [8] , but only few contributions could be found when an additional shear flow is presented [9] -[12] . Also, the influence of the shear stress at the interface has been thoroughly studied in cavity flow problems, by neglecting phase change processes. The role that these three effects-evaporation, thermo-capillarity and shear-stress could have, when acting contemporarily, remains not completely understood [3] . In this paper, we will study numerically the case of a volatile fluid evaporating when subject to a shear-stress flow. Focus will be given to the role that the evolution of the concentration boundary layer could have in determining the effective heat and mass transfer rate at the interface.
Let consider a horizontal, isothermal layer of pure volatile liquid whose interface is exposed to a flow of inert gas. To simplify the modeling efforts, the interface is considered to remain completely flat and un-deformable while being subject to a tangential stress. If evaporation is neglected, the liquid layer will show a bulk movement induced by the shear stress acting on the interface because of the presence of the inert gas flow. A steady state is then reached according to the continuity of the shear stresses at the interface. When evaporation is took into account, and then the interface begins to cool. This cooling is not uniform all along the interface because the flow of gas removes the vapor more effectively at the inlet border than elsewhere along the interface. If we focus our attention on the liquid layer, we deal with a horizontal thermal gradient that acts along the interface in the direction of the flow and a vertical one due to the general cooling of the interface that makes the layer sensitive to convective instabilities. For many fluids at the surface tension a monotonic decreasing function of the temperature, the horizontal thermal gradient is responsible for a thermo-capillary driven global bulk motion of the liquid in the direction contrary to the inert gas flow. For the sake of simplicity, we neglected the influence of gravity. If present, when the vertical thermal gradient would have exceed a critical value, a bulk convective motion in the form of recirculation rolls should have also arisen. This convective motion has strong effects on the temperature distribution of the liquid bulk phase and, as a consequence, the heat flux exchanged between the liquid and the wall can significantly change respect to the pure conductive state.
2. Numerical Model
Numerical simulations have been performed to assess the effects that the coupling between shear flows, evaporation and thermo-capillary convection could have in the heat and mass transfer characteristics at the interface of the working fluid. The commercial software Fluent complemented by the mesh generator Gambit has been used as the basic CFD solver. Specific custom-made C code, the so-called User Defined Functions, has been implemented to take into account for evaporation and thermo-capillary effects that are not included in the standard models [13] . Numerical simulations have been performed on the 3D geometry (Figure 1) consisting of a square liquid pool of 50 × 50 mm and a depth of 1.6 mm.
It is important also to stress that the two-layer problem has been studied. This means that also the thermo- fluid dynamic fields in the gas channel superposed to the liquid pool have been computed.
The number of computational points has been chosen according to a mesh sensitivity rule: tests with different mesh sizes have been performed. Solution was calculated on meshes of increasing computational points’ number.
![]()
Figure 1. The geometry considered for numerical simulations.
When the computed solution was not changing significantly then the mesh with the minimal number of points has been selected. Due to the presence of strong gradients near the interface, and the necessity to refine the mesh close to it because of evaporation, the average number of computational points resulted to be 347,000 while the hexahedral control volumes accounted to 1,100,000. The general working framework of investigation consists of a layer of pure volatile liquid in contact with an inert gas flowing at different speeds. The gas is considered as ideal and incompressible. In each phase the physic-chemical properties and transport coefficient are considered constant. Those assumptions are valid if the evaporation rate and the thermal gradient are not too large. It is supposed that both the gas and the liquid layer are of fixed thickness; for the latter to be valid during the evaporation process, it is supposed that an equivalent amount of liquid is injected instantaneously to compensate for the evaporating liquid and that the fresh liquid injected does not alter the thermo-fluid dynamic field (vanishing Peclet number). Ethanol is considered as working fluid.
The set of equations solved in the gas and liquid bulk phase is the following:
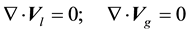 (1.1)
(1.1)
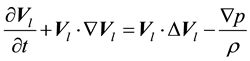 (1.2)
(1.2)
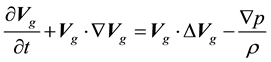 (1.3)
(1.3)
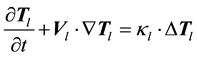 (1.4)
(1.4)
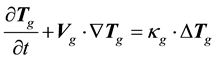 (1.5)
(1.5)
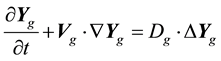 (1.6)
(1.6)
The system is closed by the following boundary conditions:
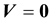 (1.7)
(1.7)
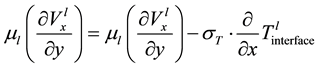 (1.8)
(1.8)
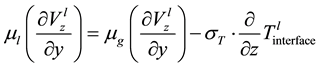 (1.9)
(1.9)
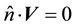 (1.10)
(1.10)
 (1.11)
(1.11)
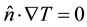 (1.12)
(1.12)
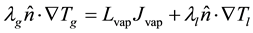 (1.13)
(1.13)
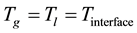 (1.14)
(1.14)
 (1.15)
(1.15)
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
To deal with the interface between the two fluids and to appropriately implement the boundary conditions, the following guidelines were applied:
1) The interface between two different zones―no matter the kind of phases it separates (e.g. liquid/liquid or liquid/gas)―is considered as a two-sided wall without thickness whose normal are positives if directed outward.
2) Neither absorption of gas in the liquid phase is considered nor evaporation of the liquid. The gas channel is considered to be filled by pure inert gas, while the liquid cavity by pure liquid.
3) The continuity of the tangential velocity components of the interfacial velocity is also implemented, by equalizing at each calculation step the velocity of the gas side of the interface to the one evaluated in the liquid from the shear stress conditions.
4) The Laplace pressure at the interface has been neglected by considering that the interface is flat and non- deformable. This assumption allows for greatly simplify the momentum conditions in direction normal to the interface.
3. Results
The evolution of the system has been studied respect to variations of the volume flow rate of the gas shear flow. Three flow rates have been investigated: 1 L/min, 4 L/min and 8 L/min. The corresponding average velocities as computed at the outlet section range between 0.04 - 0.33 m/sec, while Reynolds numbers vary between 14 and 115, the laminar character of the flow being confirmed.
One of the goals of the CFD analysis was to follow the evolution of the thermal patterns generated at the interface as result of the interaction between thermo-capillary stresses and shear flow ones. Figure 2 shows the evolution of the thermal patterns for a volumetric flow rate of 1 L/min. Pictures are taken at interval of approximately 15 seconds. It is possible to notice that at the beginning of the computation thermal patterns size is approximately 1/10 of the interface length (Figure 2(a)) and it is slowly increasing during the evolution of the interfacial thermal field. After 50 sec., the typical size of the thermal cells ranges between 1/5 and 1/10 of the interface length. The computed maximal temperature difference at the interface, i.e. the temperature difference between the coldest and hottest point at the interface is ~2.8 K.
An analogous trend could be spotted in the case of an imposed volumetric flow rate of 4 L/min. In this case, after the initial transient leading to cells formation and coalescence a quasi-steady state is reached with a typical thermal cells size of 1/4 of the interfacial length (Figure 3). The computed interfacial temperature difference accounts for ~3.9 K.
In the latter case studied, volumetric flow rate of 8 L/min (Figure 4), the transient phase is characterized by the formation of two rows of elongated cells on the lateral border of the interface. They coalesce in larger thermal cells having a characteristic size ranging between 1/3 and 1/5 of the interfacial length. In this latter case, the computed temperature difference at the interface is ~4.2 K.
In all cases, some common features appear.
・ The size of the thermal cells is increasing due to the thermal gradient relaxation in the bulk liquid. In the transient phase, the liquid layer acts as a layer cooled from above. The thermal boundary layer in the liquid bulk phase increases by thermal diffusion during the evolution of the system and as a consequence, being the characteristic number of the thermal cells approximatively proportional to the thermal gradient thickness in the bulk phase, the typical size of the thermal cells increases [14] .
・ The distribution of temperature shows a minimum at the inlet border. Along the inlet line―the line where the gas flows meet the evaporating liquid―the gas has the maximal efficiency in removing vapor from the interface. The inlet line corresponds to the line where the evaporation is maximal and the cooling effects more efficient.
・ In Figure 5 and Figure 6, the evaporation rate time evolution is plotted for the different gas flow rates studied. It is interesting to point out that:
・ The evaporation rate variation has a rapid, strong transient in a time lag of few seconds (Figure 6). At the beginning no vapor is present in the gas phase. The higher values of the evaporation rate could be explained by considering that the entropic driving force for the evaporation process to appear is strongest when the liquid is evaporating in a vapor-free gas layer.
・ The evaporation rate is increasing with increasing volumetric gas flow rate. However, this increase is not linearly proportional. More in details, the evaporation rate increase for a fourfold increase in the gas flow rate accounts only to 2.5 times. The increase is further reduced when passing to eightfold gas flow rate.
![]()
Figure 2. Thermal patterns at the interface for a volumetric gas flow of 1 L/min: (a) 1 sec; (b) 15 sec; (c) 30 sec; (d) 50 sec.
![]()
Figure 3. Thermal patterns at the interface for a volumetric gas flow of 4 L/min: (a) 1 sec; (b) 15 sec; (c) 30 sec; (d) 50 sec.
![]()
Figure 4. Thermal patterns at the interface for a volumetric gas flow of 8 L/min: (a) 20 sec; (b) 40 sec; (c) 60 sec; (d) 80 sec.
![]()
Figure 5. Evaporation rate as a function of N2 flow rate.
・ After the transient, the evaporation rate stabilizes at a quasi-steady value. This point is rather meaningful because the thermal patterns at the interface are continuing to evolve while keeping the total evaporation rate constant.
To better understand this latter point, concentration boundary layers at the center of the interfacial region have been computed and compared. Figures 7-9 show that, for all cases, the concentration boundary layer in the gas phase evolves toward a constant and steady distribution after a short transient, approximatively 2 sec. for a volumetric gas flow rate of 1 L/min, less than 1 sec. for a gas flow of 4 L/min and less than 0.5 sec. for 8 L/min.
![]()
Figure 6. Evaporation rate as a function of N2 flow rate―initial transient.
![]()
Figure 7. Concentration boundary layer evolution for a volumetric flow rate of 1 L/min.
![]()
Figure 8. Concentration boundary layer evolution for a volumetric flow rate of 4 L/min.
![]()
Figure 9. Concentration boundary layer evolution for a volumetric flow rate of 8 L/min.
By comparison with Figure 6, it could be inferred that the main driving force in the evolution of the evaporation rate at the interface is the creation and stabilization of the vapor boundary layer [15] . Evaporation from the interface is, in these conditions, diffusion limited by the efficiency of the gas flow in removing vapor from the interface.
4. Conclusion
The coupling between evaporation and thermo-capillary convection has a strong effect on the thermo-fluid-dy- namic field of a liquid layer subject to a flow of inert gas. Common features have been spotted concerning the evolution of the thermal patterns: the size dependence on the relaxation of the thermal gradient in the bulk liquid phase and the typical size of the thermal spot. Also, the evaporation rate is strongly affected by the vapour distribution in the gas phase. When the vapour boundary layer has reached a given steady state, the total evaporation rate is only barely changing by the evolution of the thermal field at the level of the interface. This result could be of importance in the designing and optimization of enhanced evaporators for cooling of electronic and power devices.
Acknowledgements
The authors would like to thank the ESA Microgravity Application Program dedicated to the evaporation phenomena and applications for the financial support in achieving the presented results.