Vibration of Three-Layered FGM Cylindrical Shells with Middle Layer of Isotropic Material for Various Boundary Conditions ()
1. Introduction
Yamanouchi et al. [1] introduced the concept of functionally graded materials (FGMs), working as aerospace researchers in Japan. Rabin and Heaps [2] reported some methods for the manufacturing of FGMs. The idea of ceramic transactions for the fabrication of FGMs was introduced by Koizumi [3] . Miyamoto et al. [4] composed a book on FGMs, in which they gave a high quality discussion on the design and applications of FGMs. Rayleigh [5] analyzed the study of Sophie on the vibration of circular cylindrical shells. Love [6] at the end of 19th century, gave the first linear shell theory based on Krichhoff’s hypothesis for plates. Arnold and Warburton [7] [8] derived equations of motion for vibration of thin circular cylindrical shells. They used Lagrange equations with strain and kinetic energy expressions to derive these equations. Forsberg [9] studied shell equations to scrutinize the effect of boundary conditions on vibration characteristics of circular cylindrical shells. In his work, exponential axial modal dependence was measured. Sewall and Naumann [10] studied analytical and experimental frequencies and mode shapes for the vibrations using the Rayleigh-Ritz method. The characteristic beam functions were used to approximate the modal dependence in the axial direction. Warburton [11] , Warburton and Higgs [12] and Goldman [13] studied the natural frequencies and mode shapes of thin cylindrical shells and selected exponential functions for the modal dependence in the axial direction. Sharma [14] explored the natural frequencies of fixed free circular cylindrical shells. He [15] also studied the problems of vibration characteristics of thin circular cylindrical shells with various end conditions with first order shell theory of Sanders. A simple variational technique was applied to give a cubic frequency equation. Loy and Lam [16] studied the vibration of thin cylindrical shells with ring supports, placed along the shell length and which imposed a zero lateral deflection. The study was carried out using Sander’s shell theory. Naeem and Sharma [17] employed an analytical procedure to study the free vibration characteristics of thin cylindrical shells. Ritz polynomial functions were assumed to satisfy the axial modal dependence and the Rayleigh Ritz variational approach was employed to formulate the general eigenvalue problem. Influence of some commonly used boundary conditions and shell parameters on the vibration frequencies were examined. Loy et al. [18] studied the vibration of FGM cylindrical shell fabricated with the constituent materials stainless steel and nickel. They concluded that the frequency characteristics were similar to those of homogeneous isotropic cylindrical shells and the frequencies were affected by the constituent volume fractions and the configurations of the constituent materials but they found the response of frequencies of FGM cylindrical shells for only simply supported boundary condition. This work was extended by Pradhan et al. [19] by studying the vibration of FGM cylindrical shell for various boundary conditions. Arshad et al. [20] [21] calculated natural frequencies of the FGM cylindrical shell by various volume fraction laws and under various boundary conditions respectively. Najafizadeh and Isvandzibaei [22] studied the vibration of thin FGM cylindrical shells with ring supports. The study was carried out based on third order shear deformation shell theory. The objective was to observe the influence of the configurations of the constituent materials, positions of the ring support and different boundary conditions on the natural frequencies of the cylindrical shells. The analysis was carried out with strain displacement relations from Love’s shell theory. The governing equations were obtained using energy functional with the Rayleigh Ritz method. Sofiyev et al. [23] studied the vibration and stability analysis of a three-layered conical shell with middle layer composed of functionally graded material. They applied Galerkin numerical technique to transform the governing equations of motion into a pair of time dependent partial differential equations. They concluded that the material parameters are directly affected by the diverse configurations of the FGM constituents and by the nature of materials used in the shell layers. He [24] extended this work to study the vibration and stability response of a composite cylindrical shell containing a functionally graded layer. Li and Batra [25] [26] investigated other dynamic aspects of shells like buckling of a three layered simply supported axially compressed laminated composite as well as isotropic thin cylindrical shells. They designed these shells in such a way that the inner and outer layers of the shells were composed of the composite and isotropic materials respectively and a layer of functionally graded material was inserted at the middle in the transverse direction. Arshad et al. [27] [28] studied the frequency spectra of bi-layered cylindrical shells by taking different materials in both layers such as isotropic as well as functionally graded materials and by taking two different functionally graded materials at the inner and outer layers of the cylindrical shells respectively.
2. Formulation of shell problem
2.1. Volume Fraction Law
Most of functionally graded materials are used in high temperature and possess temperature dependent proper-
ties. The material property  is expressed as a function temperature
is expressed as a function temperature 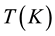 by Touloukian [29] as:
by Touloukian [29] as:
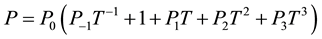 (1)
(1)
where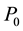 ,
, 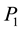 ,
, 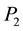 and
and 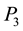 are the coefficients of temperature
are the coefficients of temperature 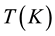 expressed in Kelvin and are unique to
expressed in Kelvin and are unique to
the constituent materials. The material properties 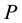 of FGMs are a function of the material properties and volume fractions of the constituents, and can be expressed as:
of FGMs are a function of the material properties and volume fractions of the constituents, and can be expressed as:
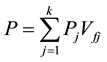 (2)
(2)
where 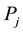 and
and 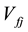 are the material property and volume fraction of the constituent material
are the material property and volume fraction of the constituent material 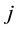 respectively. For three-layered FGM cylindrical shells, the outer and inner layers are assumed to be functionally graded and the middle layer isotropic. The shell thickness is assumed to be distributed in three portions. With this assump-
respectively. For three-layered FGM cylindrical shells, the outer and inner layers are assumed to be functionally graded and the middle layer isotropic. The shell thickness is assumed to be distributed in three portions. With this assump-
tion, the extensional, coupling and bending stiffness are modified in three layers. Let 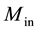 and
and 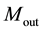 represent
represent
the inner and outer constituent materials of the FGM layers used to fabricate the three layered FGM cylindrical shell with middle layer of isotropic material. For a functionally graded material layers, consisting of two mate-
rials 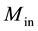 and
and ![]() , volume fraction is written for an effective material property as:
, volume fraction is written for an effective material property as:
![]() (3)
(3)
where![]() , the volume fraction, is defined for a material
, the volume fraction, is defined for a material ![]() as:
as:
![]() (4)
(4)
where ![]() is the radial variable,
is the radial variable, ![]() and
and ![]() are the inner and outer coordinates from the centre of the circular
are the inner and outer coordinates from the centre of the circular
cylindrical shell. Also ![]() and
and ![]() are the material properties of
are the material properties of ![]() and
and ![]() respectively.
respectively.
2.2. Theoretical Considerations
Consider a cylindrical shell as shown in the Figure 1(a). Let ![]() is the radius,
is the radius, ![]() is the length and
is the length and ![]() is the
is the
thickness of the cylindrical shell. The orthogonal coordinates system ![]() is taken to be at the middle sur-
is taken to be at the middle sur-
face of the shell. The ![]() -coordinate is taken in the axial direction of the shell
-coordinate is taken in the axial direction of the shell ![]() is in the circumferential and
is in the circumferential and ![]() -coordinate is in the radial direction of the shell. The deformations of the shell in axial, circumferential and
-coordinate is in the radial direction of the shell. The deformations of the shell in axial, circumferential and
radial directions are represented by![]() ,
, ![]() and
and ![]() respectively. For the study of thin cy-
respectively. For the study of thin cy-
lindrical shell, three dimensional problems are converted in to two dimensional by applying plane stress condition. The constitutive relation of stress and strain of a thin cylindrical shell is given by Hook’s law as:
![]() (5)
(5)
where ![]() is the stress vector,
is the stress vector, ![]() is the strain vector and
is the strain vector and ![]() is the reduced stiffness matrix. The stress
is the reduced stiffness matrix. The stress
vector and the strain vectors are defined as:
![]() (6)
(6)
![]() (7)
(7)
where ![]() and
and ![]() are the normal stresses in
are the normal stresses in ![]() and
and ![]() directions, and
directions, and ![]() is the shear stress on the
is the shear stress on the ![]()
-plane. Similarly ![]() and
and ![]() are the normal strains in the
are the normal strains in the ![]() and
and ![]() directions, and
directions, and ![]() is the shear strain on the
is the shear strain on the ![]() -plane. The reduced stiffness matrix is defined as:
-plane. The reduced stiffness matrix is defined as:
![]() (8)
(8)
![]() (a) (b)
(a) (b)
Figure 1. (a) Geometry of a Circular Cylindrical Shell; (b) Cross-sectional vision of three-layered cylindrical shell.
So the relation (5) can be expressed as:
![]() (9)
(9)
For isotropic materials the reduced stiffness ![]() are defined as:
are defined as:
![]() (10)
(10)
where ![]() is the Young’s modulus and
is the Young’s modulus and ![]() is the Poisson’s ratio. According to Love’s shell theory, the components in the strain vector
is the Poisson’s ratio. According to Love’s shell theory, the components in the strain vector ![]() are defined as:
are defined as:
![]() (11)
(11)
where![]() ,
, ![]() and
and ![]() are the reference surface strains.
are the reference surface strains.![]() ,
, ![]() and
and ![]() are the surface curvatures. From Equations (9) and (11) the components in the stress vector
are the surface curvatures. From Equations (9) and (11) the components in the stress vector ![]() are defined as:
are defined as:
![]() (12)
(12)
For a thin cylindrical shell the force and moment resultants are defined as:
![]() (13)
(13)
![]() (14)
(14)
where![]() ,
, ![]() and
and ![]() are force components in axial, circumferential and shear directions.
are force components in axial, circumferential and shear directions.![]() ,
, ![]() and
and
![]() are moment components in axial, circumferential and shear directions. Equations (12), (13) and (14) im-
are moment components in axial, circumferential and shear directions. Equations (12), (13) and (14) im-
plies:
![]() (15)
(15)
where ![]() and
and ![]() are defined as:
are defined as:
![]() (16)
(16)
![]() (17)
(17)
and ![]() is defined as:
is defined as:
![]() (18)
(18)
where![]() ,
, ![]() and
and ![]() are the extensional, coupling and bending stiffness matrices given as:
are the extensional, coupling and bending stiffness matrices given as:
![]()
where![]() ,
, ![]() and
and ![]() are the extensional, coupling and bending stiffness and defined as:
are the extensional, coupling and bending stiffness and defined as:
![]() (19)
(19)
The coupling stiffness ![]() become zero for isotropic cylindrical shell and is non-zero for FGM cylindrical shells. The general equations for strain energy and kinetic energy of a cylindrical shell can be written as:
become zero for isotropic cylindrical shell and is non-zero for FGM cylindrical shells. The general equations for strain energy and kinetic energy of a cylindrical shell can be written as:
![]() (20)
(20)
![]() (21)
(21)
where ![]() is the mass density per unit length and is defined as follows:
is the mass density per unit length and is defined as follows:
![]() (22)
(22)
where ![]() is the mass density of the shell material.
is the mass density of the shell material.
By substituting![]() ,
, ![]() and
and ![]() from Equations (17) and (18) in Equation (20) implies:
from Equations (17) and (18) in Equation (20) implies:
![]() (23)
(23)
2.3. Strain-displacement and Curvature-displacement Relation
A number of shell theories have arisen and are used. Among these theories however the Love’s shell theory is considered to be the first theory about shells and all other shell theories were derived from the Love’s shell theory by amending some physical terms. The strain-displacement and the curvature-displacement relations which are adopted from Love’s [6] shell theory are given as below:
![]() (24)
(24)
![]() (25)
(25)
By substituting these values of strain displacement and curvature displacement from equations (24) and (25) in equation (23), we obtain the strain energy equation in the form of displacement functions![]() ,
, ![]() ,
, ![]() and their partial derivatives as:
and their partial derivatives as:
![]() (26)
(26)
2.4. Lagrangian Energy Functional
The Lagrangian energy functional![]() , is the difference of the two types of shell energies and defined as:
, is the difference of the two types of shell energies and defined as:
![]() (27)
(27)
2.5. Rayleigh-Ritz Method
The energy variation methods i.e., Rayleigh Ritz and Galerkin methods are the most frequently used ones to analyze the shell vibrational behavior. In the Rayleigh Ritz method, the energy variational functional is minimized with respect to the coefficients of an approximating series representing the displacement deformations. Many researchers such as Sewall and Naumann [10] , Sharma and Johns [15] , Loy et al. [18] and Naeem and Sharma [17] used this procedure to analyze the vibration characteristics of the cylindrical shells.
2.6. Axial Modal Dependence
The expressions for the modal displacement deformations are presumed in the form of product of functions of space and time variables. This leads to a system of ordinary differential equations of three unknown functions of the axial space variable. Different types of functions are chosen to approximate the axial modal dependence. These functions satisfy the boundary conditions. Well-known functions are beam functions, Ritz polynomial functions, orthogonal polynomials and Fourier series of the circular functions. The expression for modal displacement deformations are assumed as:
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
In the axial, circumferential and radial directions respectively, the coefficients![]() ,
, ![]() and
and ![]() are the constants denoting the amplitudes of the vibrations in the
are the constants denoting the amplitudes of the vibrations in the![]() ,
, ![]() and
and ![]() directions respectively,
directions respectively, ![]() is the circumferential wave number and
is the circumferential wave number and ![]() is the natural angular frequency for the cylindrical shell. The axial function
is the natural angular frequency for the cylindrical shell. The axial function ![]() is chosen as the beam function as:
is chosen as the beam function as:
![]() (31)
(31)
where ![]() are some constants with value 0 or 1 chosen according to the boundary condition.
are some constants with value 0 or 1 chosen according to the boundary condition. ![]() are the roots of some transcendental equations and
are the roots of some transcendental equations and ![]() are some parameters dependent on
are some parameters dependent on![]() . Their values are given as in Table 1:
. Their values are given as in Table 1:
The geometric boundary conditions for clamped, free and simply supported boundary conditions can be expressed mathematically in terms of characteristic beam function ![]() as:
as:
Clamped boundary condition ![]()
Free boundary condition ![]()
Simply supported boundary condition ![]()
2.7. Derivation of Frequency Equation
On substituting the expressions for the deformation displacements![]() ,
, ![]() and
and ![]() in the expression for the strain and kinetic energies of the cylindrical shells and employing the principle of minimization of the energy the expression for maximum strain and kinetic energies are obtained. The new form of the Lagrangian functional is formed as:
in the expression for the strain and kinetic energies of the cylindrical shells and employing the principle of minimization of the energy the expression for maximum strain and kinetic energies are obtained. The new form of the Lagrangian functional is formed as:
![]() (32)
(32)
where
![]() (33)
(33)
![]() (34)
(34)
To derive the shell frequency equation, the energy functional is extremized with respect to the vibration amplitudes: A, B and C, resulting in three homogenous linear following equations:
![]() (35)
(35)
By re-arranging equation (35), the shell frequency equation is written in the eigenvalue form as:
![]() (36)
(36)
where the expressions for the terms![]() ’s,
’s, ![]() and
and ![]() are the given in Appendix.
are the given in Appendix.
3. Results and Discussion
A number of comparison of the results for isotropic and FGM cylindrical shells are presented to verify the validity, efficiency and accuracy of the present approach. The present analysis is carried out by using the energy variational procedure viz: Rayleigh-Ritz method. This method is based on the principle of minimization of energy. The numerical results for the following three frequently encountered sets of boundary conditions are evaluated to check the validity, efficiency and accuracy of the present technique.
![]()
Table 1. Six commonly used boundary conditions.
・ Simply supported-simply supported (SS-SS)
・ Clamped-clamped (C-C)
・ Clamped-free (C-F)
3.1. Isotropic cylindrical shells
In Table 2, the frequency parameters ![]() for an isotropic cylindrical shell is compared with
for an isotropic cylindrical shell is compared with
those ones evaluated by Swaddiwudhipong [30] for simply supported boundary conditions. The shell parameters are listed in this table. The comparison is analyzed for the cases: ![]() and
and ![]() with circumferential mode
with circumferential mode ![]() to 5. The absolute differences between the two sets of frequencies are very minute.
to 5. The absolute differences between the two sets of frequencies are very minute.
In Table 3, frequency parameter ![]() for a cylindrical shell with clamped-clamped edge conditions are compared with those evaluated by Joseph and Haim [30] Shell properties are described in the table. It is noticed that for
for a cylindrical shell with clamped-clamped edge conditions are compared with those evaluated by Joseph and Haim [30] Shell properties are described in the table. It is noticed that for![]() , the present frequencies are larger where as for
, the present frequencies are larger where as for![]() , the two frequencies are approximately equal. The fundamental frequency is associated with the circumferential mode number
, the two frequencies are approximately equal. The fundamental frequency is associated with the circumferential mode number![]() .
.
In Table 4, natural frequencies (Hz) for a clamped-free cylindrical shells are compared with those calculated experimentally by Sewall and Nauman [10] for the axial wave number![]() . Experimental values of the shell frequency are lower than the present theoretical ones. This difference may be due to the some imperfection in the experimental devices. The lowest frequency is associated with the circumferential wave numbers
. Experimental values of the shell frequency are lower than the present theoretical ones. This difference may be due to the some imperfection in the experimental devices. The lowest frequency is associated with the circumferential wave numbers ![]() for
for ![]() respectively.
respectively.
3.2. FGM cylindrical Shells
Table 5 represents a comparison of natural frequencies (Hz) for type-I FGM cylindrical shell configured according to those ones evaluated by Loy et al. [18] for simply supported boundary condition and power law exponents![]() , 1, 5. The minimum frequency occurs at the circumferential wave number
, 1, 5. The minimum frequency occurs at the circumferential wave number ![]() which is about 0.009%, 0.001% and 0.007% less than those given in [18] whereas in Type II shell, lowest frequency corresponds to circumferential wave number
which is about 0.009%, 0.001% and 0.007% less than those given in [18] whereas in Type II shell, lowest frequency corresponds to circumferential wave number ![]() which is about 0.01%, 0.009% and 0.021%, less than those evaluated in [18] . It is concluded from the above comparisons of shell frequencies that the present method is valid and efficient and gives fast and accurate results.
which is about 0.01%, 0.009% and 0.021%, less than those evaluated in [18] . It is concluded from the above comparisons of shell frequencies that the present method is valid and efficient and gives fast and accurate results.
3.3. Three-layered FGM cylindrical shells with middle layer of isotropic material
A three-layered FGM cylindrical shell whose cross section is shown in Figure 1(b), is fabricated in such a way that the inner and outer layers of the shells is fabricated with FGM layers while an isotropic material is inserted at the middle layer of the shell. The thickness of each layer is assumed to be equal. The shell material parameters include the Young’s modulus, Poisson’s ratio and the mass-density. The Young’s modulus is the most in-
fluencing the shell vibrations characteristics. In this study the Poisson’s ratio is assumed to be constant for functionally graded materials whereas the Young’s modulus is a function of the intrinsic thickness variable ![]() as well as the Young’s moduli of the constituent materials forming functionally graded layers. The thickness of each layer is supposed to be of
as well as the Young’s moduli of the constituent materials forming functionally graded layers. The thickness of each layer is supposed to be of![]() . This variation of material thickness distribution modifies the stiffness moduli such as:
. This variation of material thickness distribution modifies the stiffness moduli such as:
![]() (37)
(37)
where![]() ,
, ![]() and in(FGM), out(FGM) are associated with inner and outer functionally graded layers respectively and m(isotropic) is related with the middle isotropic layer of a cylindrical shell. Their values are given in Appendix I. If we take
and in(FGM), out(FGM) are associated with inner and outer functionally graded layers respectively and m(isotropic) is related with the middle isotropic layer of a cylindrical shell. Their values are given in Appendix I. If we take![]() ,
, ![]() constituent materials at the inner FGM layer and
constituent materials at the inner FGM layer and![]() ,
, ![]() at the outer FGM layer, the resultant material properties Young’s modulii, Poisson ratios and mass density of inner and outer FGM layers are given as:
at the outer FGM layer, the resultant material properties Young’s modulii, Poisson ratios and mass density of inner and outer FGM layers are given as:
![]() (38)
(38)
![]() (39)
(39)
By keeping isotropic material at the middle layer and by the variation of the constituents in the FGM layer as shown in Figure 1(b), four types of cylindrical shells can be formed as shown in Table 6. Material properties of the isotropic material as well as FGM constituents are given in the reference [18] [19] .
3.4. Variation of volume fractions of FGM constituents at the inner and outer FGM layers
Material properties for inner and outer FGM layers of the cylindrical shell vary from ![]() to
to ![]() and from
and from ![]() to
to ![]() respectively. From these relations, one can conclude that at
respectively. From these relations, one can conclude that at![]() , the effective material properties become
, the effective material properties become![]() ,
, ![]() ,
, ![]() whereas for
whereas for![]() , material properties become
, material properties become ![]() ,
, ![]()
![]() at the inner FGM layer and at
at the inner FGM layer and at![]() , the material properties turn into
, the material properties turn into![]() ,
, ![]() ,
, ![]() while at
while at![]() , the material properties turn into
, the material properties turn into![]() ,
, ![]() ,
, ![]() for functionally graded outer layer of the cylindrical shell.
for functionally graded outer layer of the cylindrical shell.
These results conclude that the material properties vary smoothly and continuously of constituent materials
![]() and
and ![]() from the inner surface to
from the inner surface to ![]() and
and ![]() to the outer surface of both the FGM layers respective-
to the outer surface of both the FGM layers respective-
ly. Similar response of the material properties is seen in the inverse direction. Variation of volume fractions![]() ,
,
![]() and
and![]() ,
, ![]() of constituent materials
of constituent materials![]() ,
, ![]() and
and![]() ,
, ![]() placed at the inner and the outer shell sur-
placed at the inner and the outer shell sur-
faces at the inner and outer FGM layers respectively of the shell are sketched in Figure 2(a), Figure 2(b) of the three-layered cylindrical shells. In Figure 2(a), variation of volume fractions ![]() and
and ![]() of the constituent materials
of the constituent materials ![]() and
and ![]() are sketched for the shell inner FGM layer. In this layer, the volume fraction
are sketched for the shell inner FGM layer. In this layer, the volume fraction ![]() of constituent material
of constituent material ![]() declines from its highest value 1 to its lowest value 0 whereas the volume fraction
declines from its highest value 1 to its lowest value 0 whereas the volume fraction ![]() of material
of material ![]() rises from 0 to 1 in the thickness interval
rises from 0 to 1 in the thickness interval![]() . Similar behaviour of volume fractions
. Similar behaviour of volume fractions ![]() and
and ![]() of the FGM constituents
of the FGM constituents ![]() and
and ![]() is shown in Figure 2(b) for the shell outer FGM layer. Volume fraction
is shown in Figure 2(b) for the shell outer FGM layer. Volume fraction ![]() of material
of material ![]() reduces from 1 to 0 and volume fraction
reduces from 1 to 0 and volume fraction ![]() of constituent
of constituent
material ![]() advances from 0 to its maximum value 1 in the thickness variable interval
advances from 0 to its maximum value 1 in the thickness variable interval ![]()
respectively. The middle layer is made up with some isotropic material, whose thickness span over the interval
![]() .
.
Now to study the influence of power law exponent ![]() on the volume fraction of the constituents in the FGM
on the volume fraction of the constituents in the FGM
layers, ![]() and
and ![]() are pure while
are pure while ![]() and
and ![]() have zero concentration at the inner surface of the inner
have zero concentration at the inner surface of the inner
![]()
Table 6. Configuration of types of FGM cylindrical shells.
![]()
![]() (a) (b)
(a) (b)
Figure 2. (a) Variation of volume fractions FGM1 & FGM2 of Materials M1 and M2 at the inner FGM layer of the three layered cylindrical shells; (b) Variation of volume fractions FGM3 & FGM4 of Materials M3 and M4 at the outer FGM layer of the three layered cylindrical shells.
and outer FGM layers. Similar but opposite behaviour of the FGM constituents is observed at outer surface of both the layers. For the thickness interval ![]() and p < 1,
and p < 1, ![]() decreases while
decreases while ![]() increase rapidly whereas for
increase rapidly whereas for ![]() and
and![]() ,
, ![]() decreases while
decreases while ![]() increases slowly and constantly. For the thickness interval
increases slowly and constantly. For the thickness interval ![]() and
and![]() ,
, ![]() decreases while
decreases while ![]() increases gradually but for
increases gradually but for ![]() and
and![]() ,
, ![]() decreases and
decreases and ![]() increases swiftly. Eventually,
increases swiftly. Eventually, ![]() and
and ![]() approach to their minimum and maximum values 0 and 1 respectively. Similar behaviour of volume fractions
approach to their minimum and maximum values 0 and 1 respectively. Similar behaviour of volume fractions ![]() and
and ![]() of the constituent materials
of the constituent materials ![]() and
and ![]() are observed in the outer FGM layer of the three layered cylindrical shell containing middle layer of isotropic material but in this case thickness interval changes from
are observed in the outer FGM layer of the three layered cylindrical shell containing middle layer of isotropic material but in this case thickness interval changes from![]() .
.
3.5. Frequency analysis of FGM cylindrical shell
In this section variation of natural frequencies (Hz) for four types of shell described in the above table will be discussed. The boundary conditions are taken to be simply supported-simply supported (SS-SS), clamped-clamed (C-C) and clamped-free (C-F).
3.5.1. Variation of natural frequencies (Hz) against circumferential wave number for SS-SS, C-C and C-F boundary conditions
In table 7, the variation of natural frequencies (Hz) for three sets of boundary conditions i.e. simply supported-simply supported (SS-SS), clamped-clamped (C-C) and clamped-free(C-F) are studied against the circumferential wave number![]() . In these types of shells the inner and outer layers are composed of the constituents nickel and zirconia while the middle isotropic layer is made of stainless steel. The shell parameters are
. In these types of shells the inner and outer layers are composed of the constituents nickel and zirconia while the middle isotropic layer is made of stainless steel. The shell parameters are![]() ,
, ![]() ,
, ![]() and
and![]() . It is seen that the natural frequency first decreases and after at-
. It is seen that the natural frequency first decreases and after at-
![]()
Table 7. Variation of natural frequencies (Hz) against circumferential wave number ![]() for shells I, II, III, IV
for shells I, II, III, IV ![]() .
.
taining its minimum value it begins to increase with the circumferential wave number![]() . It is also noticed that the natural frequencies for three boundary conditions become closer and closer with the increase of circumfe- rential wave number n. The frequencies associated with the clamped-free boundary condition are the lowest among those with the clamped-clamped and simply supported-simply supported boundary conditions. The variation of the frequency is similar to that of an isotropic shell.
. It is also noticed that the natural frequencies for three boundary conditions become closer and closer with the increase of circumfe- rential wave number n. The frequencies associated with the clamped-free boundary condition are the lowest among those with the clamped-clamped and simply supported-simply supported boundary conditions. The variation of the frequency is similar to that of an isotropic shell.
3.5.2. Variation of natural frequencies (Hz) against length-to-radius ratio
In Table 8, the variation of natural frequencies (Hz) against length-to-radius ratio ![]() of the four types of three-layered cylindrical shells are studied for three boundary conditions simply supported-simply supported, clamped-clamped and clamped-free. The shell parameters are
of the four types of three-layered cylindrical shells are studied for three boundary conditions simply supported-simply supported, clamped-clamped and clamped-free. The shell parameters are ![]() with circumferential wave number
with circumferential wave number ![]() and the fundamental axial mode
and the fundamental axial mode![]() .
.
From tables it is observed that the natural frequency (Hz) for all three boundary conditions decreases with the increase of length to radius ratio. It is also seen that the frequencies related to the clamped-clamped boundary conditions are greater than the simply supported-simply supported and clamped-free boundary conditions and the difference between the frequencies for all boundary conditions becomes very negligible at![]() .
.
3.5.3. Variation of natural frequencies (Hz) against thickness-to-radius ratio
In Table 9, variation of natural frequencies of the three-layered cylindrical shell is calculated against the thickness-to-radius ratio under the three selected boundary conditions i.e. simply supported-simply supported, clamped-clamped and clamped-free. In this observation the shell geometrical parameters are![]() , the fundamental axial mode is
, the fundamental axial mode is![]() , and the circumferential wave number
, and the circumferential wave number![]() . From tables it is seen that the
. From tables it is seen that the
![]()
Table 8. Variation of natural frequencies (Hz) against ![]() ratios for shell I, II, III, IV
ratios for shell I, II, III, IV![]() .
.
![]()
Table 9. Variation of natural frequencies (Hz) against ![]() ratios for shell I.
ratios for shell I.![]() .
.
natural frequencies for all three boundary conditions are very close to each other. For every boundary condition, it is also observed from the tables that the natural frequencies increase as the thickness-to-radius ratio increase.
Appendix
![]()
![]()
![]()
![]()
![]()
where
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
NOTES
*Corresponding author.