The Global Attractors of the Solution for 2D Maxwell-Navier-Stokes with Extra Force Equations

Cuicui Tian, Meixia Wang, Guoguang Lin^*

Department of Mathematics, Yunnan University, Kunming, China.

DOI: 10.4236/ijmnta.2014.35024                

Abstract

In this paper, we studied the solution existence and uniqueness and the attractors of the 2D Maxwell-Navier-Stokes with extra force equations.

Keywords

Maxwell-Navier-Stokes Equations, Existence, Uniqueness, Attractor

1. Introduction

In recent years, the Maxwell-Navier-Stokes equations have been studied extensively, and the studies have obtained many achievements [1] [2] . The Maxwell-Navier-Stokes equations are a coupled system of equations consisting of the Navier-Stokes equations of fluid dynamics and Maxwell’s equations of electromagnetism. The coupling comes from the Lorentz force in the fluid equation and the electric current in the Maxwell equations. In [1] , the authors studied the non-resistive limit of the 2D Maxwell-Navier-Stokes equations and established the convergence rate of the non-resistive limit for vanishing resistance by using the Fourier localization technique. In [2] , the author has proved the existence and uniqueness of global strong solutions to the non-resistive of the

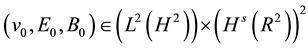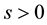2D Maxwell-Navier-Stokes equations for initial data with. The

long time behaviors of the solutions of nonlinear partial differential equations also are seen in [3] -[10] .

In this paper,we will study the 2D Maxwell-Navier-Stokes equations with extra force and dissipation in a bounded area under homogeneous Dirichlet boundary condition problems:

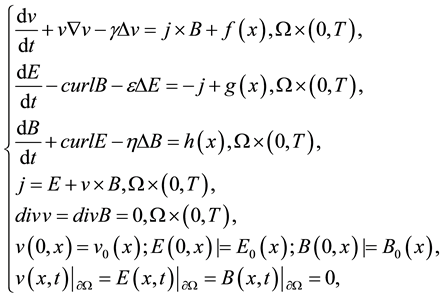(1.1)

here 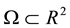is bounded set, 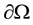is the bound of, is the velocity of the fluid, 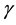is the viscosity, 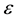and 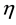are resistive constants, 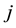is the electric current which is given by Ohm’s law, 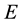is the electric field, 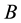is the magnetic field and 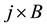is the Lorentz force.

Let 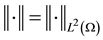and.

2. The priori estimate of solution of questions (1.1)

Lemma 1. Assume so the solution of the Dirichlet

bound questions (1.1) satisfies

here.

Proof. For the system (1.1) multiply the first equation by with both sides and obtain

(2.1)

For the system (1.1) multiply the second equation by with both sides and obtain

(2.2)

For the system (1.1) multiply the third equation by with both sides and obtain

(2.3)

Because, so is

(2.4)

According to Poincare’s inequality, we obtain

(2.5)

According to, we obtain

(2.6)

According to Young’s inequality, we obtain

(2.7)

(2.8)

(2.9)

From (2.4) (2.5) (2.6) (2.7) (2.8) (2.9), we obtain

so

Let, according that we obtain

so

Using the Gronwall’s inequality, the Lemma 1 is proved.

Lemma 2. Under the condition of Lemma 1, and ,

so the solution of the Dirichlet bound questions (1.1) satisfies

here

Proof. For the system (1.1) multiply the first equation by with both sides and obtain

(2.10)

For the system (1.1) multiply the second equation by with both sides and obtain

(2.11)

For the system (1.1) multiply the third equation by with both sides and obtain

(2.12)

According and (2.10) (2.11) (2.12) we obtain

(2.13)

here

so

According to the Sobolev’s interpolation inequalities

so

(2.14)

(2.15)

According to the Sobolev’s interpolation inequalities and Young’s inequalities

(2.16)

According to the Holder’s inequalities and inequalities

(2.17)

and

(2.18)

According to the (2.13) (2.14) (2.15) (2.16) (2.17) (2.18), we obtain

(2.19)

here

According to the Poincare’s inequalities

(2.20)

According to the Young’s inequalities

(2.21)

In a similar way,we can obtain

(2.22)

(2.23)

From (2.19)-(2.23), we have

Let, because, so existing satisfied

So

According to the Gronwall’s inequality,we can get the Lemma 2.

3. Solution’s existence and uniqueness and attractor of questions (1.1)

Theorem 1. Assume that and so questions (1.1) exist a unique

solution

Proof. By the method of Galerkin and Lemma 1 - Lemma 2, we can easily obtain the existence of solutions. Next, we prove the uniqueness of solutions in detail.

Assume are two solutions of questions (1.1), let

. Here so the diffe-

rence of the two solution satisfies

The two above formulae subtract and obtain

(3.1)

For the system (3.1) multiply the first equation by with both sides and obtain

(3.2)

For the system (3.1) multiply the second equation by with both sides and obtain

(3.3)

For the system (3.1) multiply the third equation by with both sides and obtain

(3.4)

According to (3.2) + (3.3) + (3.4), we obtain

(3.5)

here, and so

From that, we have

(3.6)

(3.7)

Notice that

(3.8)

From the (3.5), (3.6), (3.7) and (3.8), we can obtain

Let

so, we have

According to the consistent Gronwall inequality, the uniqueness is proved.

Theorem 2. [8] Let be a Banach space, and are the semigroup operators on.

here is a unit operator. Set satisfy the follow

conditions.

1) is bounded. Namely, it exists a constant, so that

;

2) It exists a bounded absorbing set namely it exists a constant so that

;

3) When is a completely continuous operator.

Therefor, the semigroup operators exist a compact global attractor.

Theorem 3. Under the assume of Theorem 1, questions (1.1) have global attractor

is the bounded absorbing set of and satisfies

1)

2) here and it is a bounded set,

Proof. Under the conditions of Theorem 1 and Theorem 2, it exists the solution semigroup of ques-

tions (1.1),

From Lemma 1 - Lemma 2, to is a bounded set that includes in the ball

This shows is uniformly bounded in

Furthermore, when there is

therefore,

is the bounded absorbing set of semigroup

Since is tightly embedded, which is that the bounded set in is the tight set in

, so the semigroup operator to is completely continuous.

4. Discussion

If we want to estimate the Hausdorff and fractal dimension of the attractor A of question (1.1), we need proof of the solution of question (1.1) that is differentiable. We are studying the solution’s differentiability hardly and positively. Over a time, we will get some results.

Acknowlegements

This work is supported by the National Natural Sciences Foundation of People's Republic of China under Grant 11161057.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Zhang, Q. (2013) On the Non-Resistive Limit of the 2D Maxwell-Navier-Stokes Equations. Journal of Mathematical Analysis and Applications, 404, 150-160. http://dx.doi.org/10.1016/j.jmaa.2013.03.011
[2]	Masmoudi, N. (2010) Global Well Posedness for the Maxwell-Navier-Stokes System in 2D. Journal de Mathématiques Pures et Appliquées, 93, 559-571. http://dx.doi.org/10.1016/j.matpur.2009.08.007
[3]	Tian, L.X. (1994) Attractor of the Dissipated and Isolated Wave-Equation. Journal of Applied Mathmatics and Mechanics, 15, 539-547.
[4]	Dai, Z.D., Guo, B.L. and Lin, G.G. (1998) Breakdown Structure of Generalized Kuramoto-Sivashinsky Equation Attractor. Applied Mathmatics and Mechanics, 19, 243-255.
[5]	Du, X.Y. and Dai, Z.D. (2000) Global Attractor of Dissipative KDV Equation about Cauchy Problem. Acta Mathematica Scientia, 20, 289-295.
[6]	Guo, B.L. (2000) The Infinite Dimension System. National Defense Industry Press, Beijing.
[7]	Wu, J.Z., Zhao, P. and Lin, G.G. (2010) An Inertial Manifold of the Damped Boussinesq Equation. Journal of Yunnan University, 32, 310-314.
[8]	Lin, G.G. (2011) Nonlinear Evolution Equations. Yunnan University Press, Kunming.
[9]	Tian, L.X. and Ding, D.P. (2000) Local Property or Weakly Damped Forced KDV Equation in 2-D Thin Domin. Journal of Jiangsu University of Sciencend Technology, 21, 106-110.
[10]	Dang, J.B., Wang, L. and Lin, G.G. (2010) Global Attractor for Weekly Damped Generalized Equation in the Long Time. Journal of Mathematical Study, 43, 1-11.